Обыкновенные дифференциальные уравнения Общие понятия

Теория дифференциальных уравнений возникла в трудах великих ученых XIIV века И. Ньютона (1642–1727) и Г.В. Лейбница (1646–1716). Сам термин «дифференциальное уравнение» ввел Лейбниц (впервые в письме к Ньютону от 1676г., а с 1684г. – в печати). К настоящему времени теория дифференциальных уравнений, включающая как обыкновенные так и уравнения в частных производных, стала основным аппаратом математического естествознания. Это объясняется тем, что многие природные явления и технологические процессы с помощью дифференциальных уравнений моделируются проще, а результаты решения соответствующих задач полнее отражают изучаемые явления и процессы по сравнению с другими методами. К достоинствам подхода, основанного на применении дифференциальных уравнений и связанных с ними начальных и краевых задач, следует отнести принципиальную возможность уточнения рассматриваемых моделей, что особенно важно в век «высоких технологий». Главная трудность в применении теории заключается в том, что не существует единого способа получения решений дифференциальных уравнений. Поэтому исключительно важное значение имеют вопросы терминологии и классификации дифференциальных уравнений.

Дифференциальным уравнением называется соотношение, связывающая неизвестную функцию, независимые переменные и производные (или дифференциалы) от неизвестной функции по этим переменным. Если неизвестная функция зависит от нескольких независимых переменных, то дифференциальное уравнение естественно содержит частные производные и называется уравнением в частных производных. Уравнения, содержащие производные лишь по одной из независимых переменных называются обыкновенными дифференциальными уравнениями. Не умаляя общности, в таких уравнениях обыкновенно считают неизвестную функцию зависящей лишь от одной независимой переменной, только от одного аргумента.

Обыкновенным дифференциальным уравнением n-го порядка общего вида называется соотношение

(1)

между независимым переменным x, его функцией y и производными . Функция называется решением этого дифференциального уравнения, если после замены y на , на ,…, на оно обращается в тождество.

Проинтегрировать дифференциальное уравнение – значит найти все функции у, удовлетворяющие этому уравнению, т.е. решить его. Операцию взятия неопределенного интеграла называют квадратурой (этот устарелый термин применяют, чтобы избежать путаницы с процессом нахождения всех решений – интегрированием дифференциального уравнения).

Общим решением дифференциального уравнения (1) называется функция, удовлетворяющая этому уравнению вида

(2)

Здесь С₁, С₂,…, С_n – произвольные постоянные (интегрирования).

Частным решением называется решение, получаемое из общего, если в последнем придать произвольным постоянным определенные числовые значения.

Общим интегралом дифференциального уравнения (1) называется соотношение

(3)

неявно определяющее общее решение этого уравнения. Иначе, общий интеграл уравнения (1) это такое соотношение (3), что, если продифференцировать его последовательно n раз по переменной х, а затем из полученных уравнений и данного соотношения исключить произвольные постоянные , то получится уравнение (1). Разрешая общий интеграл относительно у, находим общее решение; давая в общем интеграле произвольным постоянным определенные числовые значения, находим частный интеграл.

Общий интеграл представляет семейство линий на плоскости, зависящее от n параметров; дифференциальное уравнение выражает общее свойство всех линий семейства.

Уравнение (1) в некоторых случаях может иметь особое решение. Особым называется такое решение, которое не получается из общего ни при каких значениях произвольных постоянных.

Примеры.

1. – обыкновенное дифференциальное уравнение третьего порядка, нетрудно проверить, что - частное решение.

2. – уравнение первого порядка, также непосредственной проверкой убеждаемся, что - частное, а - общее решение этого уравнения.

3. – уравнение второго порядка (линейное с постоянными коэффициентами, однородное, если продолжить классификацию), его общим решением является

,

а выражение

суть общий интеграл этого уравнения. Проверим это, дважды дифференцируя по переменной х

,

и вычитая из последнего соотношения общий интеграл, немедленно находим

.

Проинтегрировать данное уравнение (найти его общий интеграл) можно, например, применяя вариант технического приема, известного как метод понижения порядка. Пусть – сложная функция переменной х, положим

; тогда .

Преобразованное дифференциальное уравнение будет

или .

Квадратурой находим

, , .

Общее решение преобразованного уравнения

, ,

после обратной замены , приводит к дифференциальному уравнению

или .

С использованием формул обратных гиперболических функций (на математическом сленге называемых «длинный логарифм»)

,

,

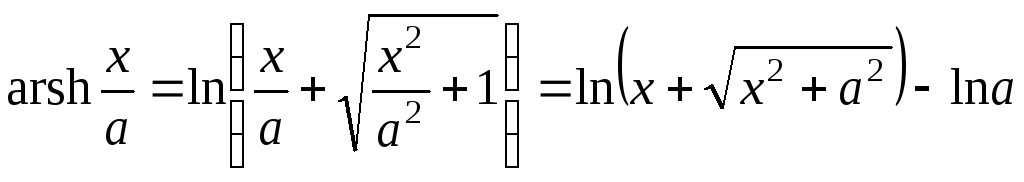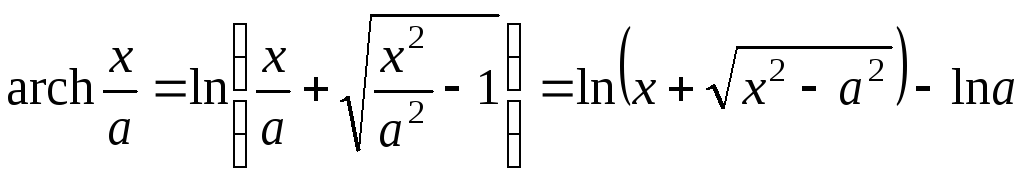второй квадратурой получаем искомый общий интеграл

, ,

в котором С₁, С₂ – произвольные постоянные. Дифференцируя общий интеграл по х, считая у функцией от х, и преобразуя, найдем первое соотношение

, .

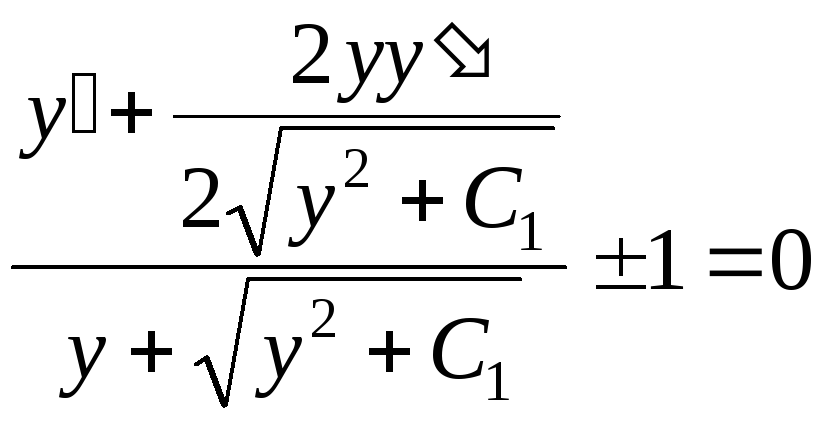Еще раз дифференцируя по х, найдем второе соотношение

, ,

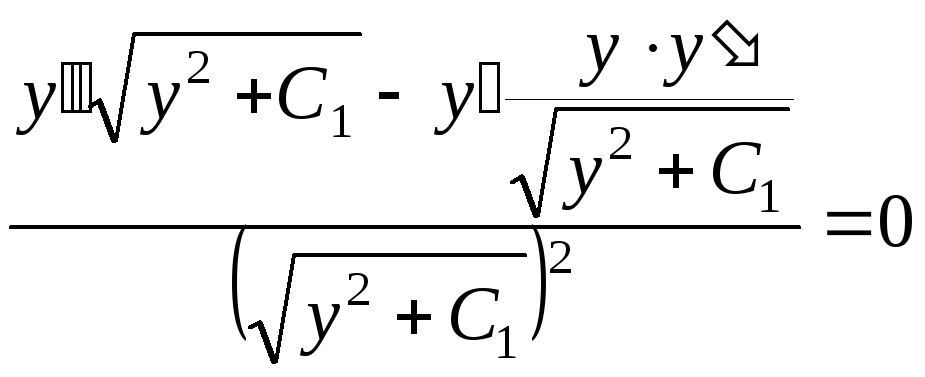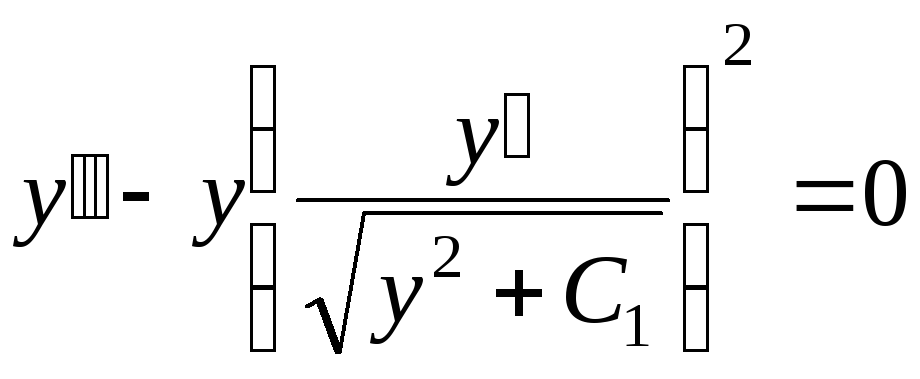комбинируя которое совместно с первым соотношением, приходим к данному дифференциальному уравнению.

Рассмотренный пример наглядно демонстрирует: во-первых, силу метода (одного из многих, применяемых в теории дифференциальных уравнений); во-вторых, какие причудливые формы может принимать один и тот же общий интеграл даже в случае относительно простого дифференциального уравнения. Вместе с тем, этот пример весьма убедительно доказывает насколько важно придерживаться правильной классификации уравнений и задач, разработанный поколениями математиков, чтобы избегать неоправданных технических трудностей при получении нужных решений.

4. Пусть – общий интеграл. Дифференцируя последовательно, найдем

; .

Последнее уравнение уже не содержи произвольных постоянных и представляет собой дифференциальное уравнение всех прямых на плоскости.

5. Найти дифференциальное уравнение всех окружностей на плоскости; выделить случай окружностей постоянного радиуса R.

Семейство всех окружностей на плоскости имеет вид

,

где a, b, R – произвольные постоянные. Данное соотношение является общим интегралом некоторого дифференциального уравнения третьего порядка. Если считать, что R – заданный параметр и только величины a, b произвольные постоянные, то данное соотношение будет общим интегралом некоторого дифференциального уравнения второго порядка. Найдем это уравнение. Дифференцируем общий интеграл дважды по х

,

,

далее ; .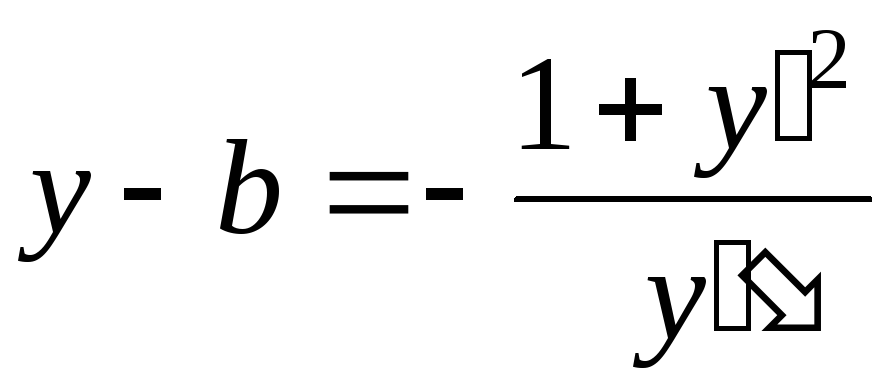

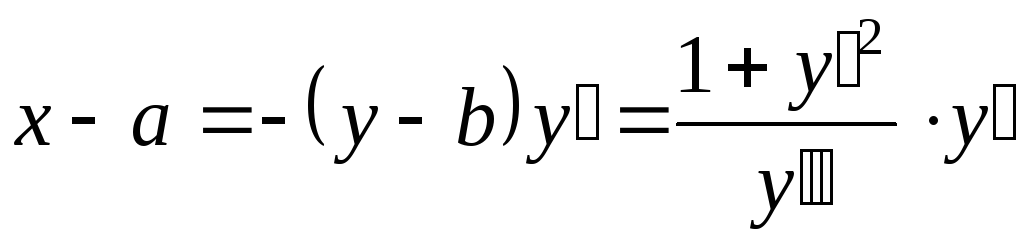Подставляем полученные выражения в общий интеграл

, ,

считая радиус положительной величиной, находим дифференциальное уравнение окружностей постоянного радиуса

,

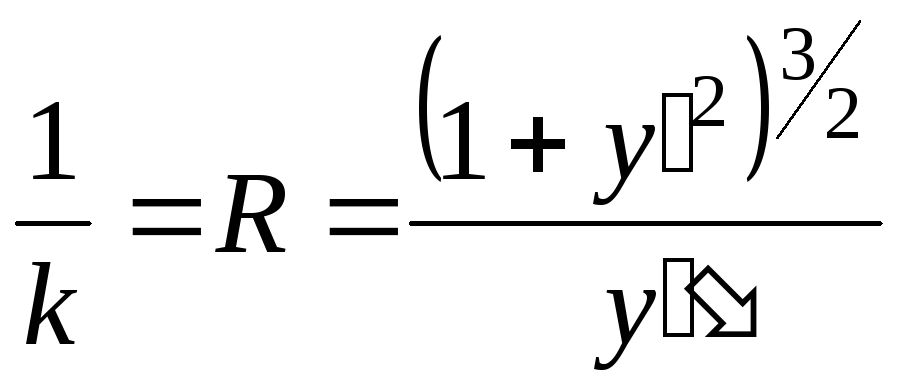здесь через k обозначена кривизна кривой .

Дифференцируя это уравнение еще раз, находим решение поставленной задачи в виде

.

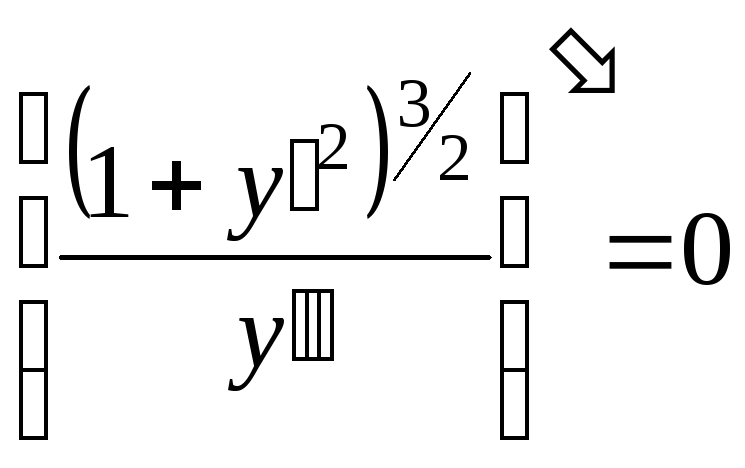Заметим, что для семейства всех прямых на плоскости (пример 4) дифференциальное уравнение выражает общее свойство семейства, заключающееся в том, что кривизна всех этих линий равна нулю. В данном примере дифференциальное уравнение всех окружностей на плоскости показывает, что для каждой линии семейства кривизна постоянна во всех точках. Такой вид уравнения оправдан тем, что служит иллюстрацией независимого вывода хорошо известной в курсе математического анализа формулы кривизны плоской кривой. Обычно это дифференциальное уравнение третьего порядка записывается иначе

.

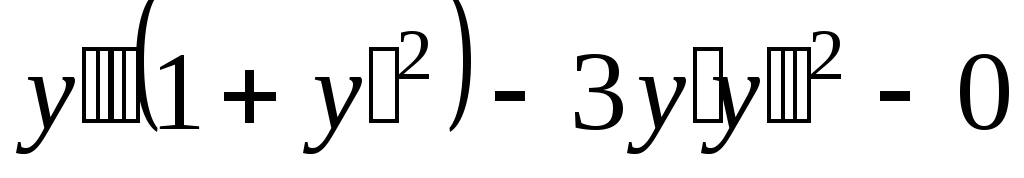6. – нелинейное дифференциальное уравнение первого порядка. Для нахождения его решений применим неожиданный технический прием. Продифференцируем его по переменной х

, отсюда , тогда:

или a) , , , ;

или b) , , , , .

Непосредственной подстановкой в исходное уравнение убеждаемся в том, что:

a) если , то – особое (частное) решение;

b) если , , то – общее решение.

Как известно, основной задачей теории дифференциальных уравнений является разыскание всех решений данного дифференциального уравнения и изучение свойств этих решений. Эта задача трудна не только для уравнения (1), но остается трудной и для уравнения первого порядка общего вида

. (4)

Более того, основная задача теории остается неразрешимой в квадратурах (за исключением некоторых классов) даже для частного случая уравнения (4)

, (5)

которое по классификации называется «обыкновенное дифференциальное уравнение первого порядка, разрешенное относительно производной». Рассмотрим подробнее уравнения вида (5), поскольку для них имеется хорошо разработанная теория. С другой стороны, большинство возникающих на практике дифференциальных уравнений (1) могут быть сведены различными методами (с применением теорем о неявной функции) к системам, имеющим нормальную форму Коши – к нормальным системам вида

, .