
- •Обыкновенные дифференциальные уравнения Общие понятия
- •Уравнения первого порядка, разрешенные относительно производной
- •Геометрическая интерпретация. Понятие о задаче Коши
- •Уравнение, не содержащее искомой функции
- •Уравнение, не содержащее независимой переменной
- •Уравнение с разделяющимися переменными
- •Однородное уравнение
- •Уравнение в полных дифференциалах
- •Линейное уравнение
- •Уравнение Бернулли
- •Уравнения первого порядка, не разрешенные относительно производной Основные понятия и определения
Уравнение с разделяющимися переменными
Уравнение с разделенными переменными
![]() , (22)
, (22)
где функции
![]() и
и
![]() непрерывны, не имеют особых решений.
Общий интеграл такого уравнения
пишется сразу
непрерывны, не имеют особых решений.
Общий интеграл такого уравнения
пишется сразу
![]() , (23)
, (23)
или в форме Коши
 . (24)
. (24)
Если
![]() и
и
![]() не равны нулю одновременно, то решение
задачи Коши можно получить, полагая С
= 0 в форме (24). Если же
не равны нулю одновременно, то решение
задачи Коши можно получить, полагая С
= 0 в форме (24). Если же
![]() ,
то требуются дополнительные исследования,
поскольку точка
,
то требуются дополнительные исследования,
поскольку точка
![]() может оказаться особой точкой
уравнения (22), а значит, единственное
решение с начальными данными x0,
y0 может не
существовать.
может оказаться особой точкой
уравнения (22), а значит, единственное
решение с начальными данными x0,
y0 может не
существовать.
Уравнение с разделяющимися переменными. Дифференциальное уравнение
![]() ,
,
в котором непрерывные
функции
![]() и
и
![]() могут быть представлены в виде произведения
функций, зависящих только от одного
аргумента
могут быть представлены в виде произведения
функций, зависящих только от одного
аргумента
![]() ,
,
![]() ,
,
то есть дифференциальное уравнение
![]() (25)
(25)
называется уравнением с разделяющимися переменными.
Предполагая, что
![]() ,
,
![]() ,
путем деления на произведение
,
путем деления на произведение
![]() уравнение (25) приводится к уравнению с
разделенными переменными
уравнение (25) приводится к уравнению с
разделенными переменными
![]() .
.
Общим интегралом этого уравнения, а следовательно, и уравнения (25), будет
![]() (26)
(26)
или
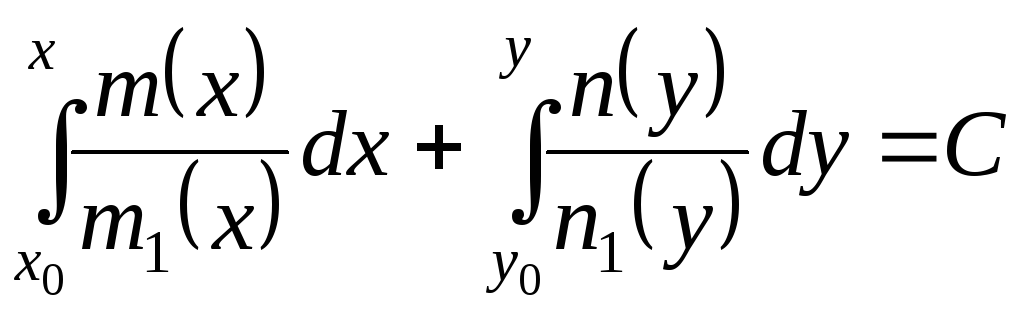 . (27)
. (27)
Предположение
![]() ,
,
![]() ,
может привести к потери частных решений.
Если уравнения
,
может привести к потери частных решений.
Если уравнения
![]() и
и
![]() имеют вещественные решения
имеют вещественные решения
![]() и
и
![]() ,
то
,
то
![]() (при
(при
![]() )
и
)
и
![]() (при
(при
![]() )
будут решениями уравнения (25). Эти
решения, и только они, могут оказаться
особыми, что проверяется дополнительным
исследованием.
)
будут решениями уравнения (25). Эти
решения, и только они, могут оказаться
особыми, что проверяется дополнительным
исследованием.
Решение задачи
Коши с начальными данными x0,
y0 при условии
![]() ,
,
![]() ,
а
,
а
![]() и
и
![]() не равны нулю одновременно, можно
получить из формулы (27), полагая С =
0. Если
не равны нулю одновременно, можно
получить из формулы (27), полагая С =
0. Если
![]() ,
то не гарантируется ни существование
ни единственность решения.
,
то не гарантируется ни существование
ни единственность решения.
Единственность
не нарушается когда начальная точка
![]() лежит на одном из частных решений
вида
лежит на одном из частных решений
вида
![]() (
(![]() ),
),
![]() (
(![]() ).
).
Наконец, поле
направлений в точке
![]() не определено, к этой точке примыкают
решения
не определено, к этой точке примыкают
решения
![]() (
(![]() ),
),
![]() (
(![]() ).
).
Уравнение вида
![]() (28)
(28)
есть уравнение с разделяющимися переменными. Общий интеграл получается после разделения переменных квадратурой
![]() . (29)
. (29)
Если уравнение
![]() имеет вещественные решения вида
имеет вещественные решения вида
![]() ,
то прямые
,
то прямые
![]() будут решениями уравнения (28). Эти решения
могут оказаться особыми, других
особых решений быть не может.
будут решениями уравнения (28). Эти решения
могут оказаться особыми, других
особых решений быть не может.
Уравнение с функцией специального вида
![]() , (30)
, (30)
где a,
b, c
– постоянные, заменой переменных
![]() преобразуется в уравнение с разделяющимися
переменными.
преобразуется в уравнение с разделяющимися
переменными.
Примеры.
18.
![]() .
Разлагая коэффициенты данного уравнения
на множители, убеждаемся, что это
уравнение с разделяющимися переменными
(25)
.
Разлагая коэффициенты данного уравнения
на множители, убеждаемся, что это
уравнение с разделяющимися переменными
(25)
![]() .
.
Разделяя переменные, запишем общий интеграл в форме (26)
![]()
или
![]() .
.
Подстановкой в исходное уравнение убеждаемся, что х = 1 и у = 1 являются частными решениями. Особых решений нет.
19.
![]() .
Уравнение определено в полосе
.
Уравнение определено в полосе
![]() ,
,
![]() .
Общий интеграл получаем после разделения
переменных
.
Общий интеграл получаем после разделения
переменных
![]() ,
, ![]() .
.
Подстановкой в
исходное уравнение убеждаемся, что
линии
![]() являются решениями этого уравнения,
более того, они являются огибающими
интегрального семейства кривых и потому
особыми решениями.
являются решениями этого уравнения,
более того, они являются огибающими
интегрального семейства кривых и потому
особыми решениями.
20.
![]() .
Путем деления на произведение
.
Путем деления на произведение
![]() данное уравнение приводится к уравнению
с разделенными переменными (22)
данное уравнение приводится к уравнению
с разделенными переменными (22)
![]() .
.
Используя формулу
(23), сразу находим общий интеграл
![]() ,
,
который для удобства записи окончательного результата перепишем в виде
![]() ,
,
или, потенцируя,
![]() ,
,
![]() .
.
Общий вид семейства
интегральных кривых показан на рис. 10.
Прямые
![]() ,
,
![]() являются частными решениями данного
уравнения, формально они не получаются
из квадратуры, поскольку
являются частными решениями данного
уравнения, формально они не получаются
из квадратуры, поскольку
![]() ,
но могут быть присоединены к общему
интегралу уравнения (если положить
,
но могут быть присоединены к общему
интегралу уравнения (если положить
![]() ).
).
Замечание. В
геометрических вопросах и при нахождении
общих интегралах выгоднее считать х
и у равноправными и принимать за
независимое переменное то х, то у
(как удобнее). Наоборот, в исследованиях
теоретико-функционального характера
(доказательство существования решения
или единственности решения начальной
задачи) всегда надо рассматривать у
как функцию от х; тогда, конечно,
ранее упоминавшиеся (27) прямые
![]() не являются решениями.
не являются решениями.
21. Найти решение
![]() дифференциального уравнения
дифференциального уравнения
![]() ,
,
удовлетворяющее начальному условию
![]() .
.
Нетрудно видеть,
что функция
![]() непрерывно по переменным х и у
в любой области конечного диаметра, а
значит всегда существует и при том
единственное решение задачи Коши. Оно
может быть найдено квадратурой (29)
записанной в форме Коши, если положить
непрерывно по переменным х и у
в любой области конечного диаметра, а
значит всегда существует и при том
единственное решение задачи Коши. Оно
может быть найдено квадратурой (29)
записанной в форме Коши, если положить
![]()
![]() ,
,
![]() ,
,
![]() .
.
Если в качестве
начального условия взять
![]() ,
то получится единственное тривиальное
(вырожденное) решение
,
то получится единственное тривиальное
(вырожденное) решение
![]() .
.
22.
![]() .
Это уравнение вида (30).
.
Это уравнение вида (30).
Положим
![]() .
Тогда
.
Тогда
![]() .
Используя исходное уравнение, имеем
.
Используя исходное уравнение, имеем
![]() ,
разделяя переменные
,
разделяя переменные
![]() ,
,
квадратурой
![]() находим общий интеграл
находим общий интеграл
![]() или
или
![]() ,
,
![]() .
Возвращаясь к старым переменным и
преобразуя, находим общее решение
.
Возвращаясь к старым переменным и
преобразуя, находим общее решение
![]() .
.
