Уравнение в полных дифференциалах

Интегрирование уравнения в полных дифференциалах

Выражение

называется полным дифференциалом, если существует такая функция , что справедливо тождество

.

Последнее тождество равносильно двум следующим

, . (43)

В частном случае, когда левая часть дифференциального уравнения

(7)

представляет полный дифференциал некоторой функции (для которой выполняются равенства (43), то говорят, что задано уравнение в полных (точных) дифференциалах и, следовательно, уравнение (7) принимает вид

.

Если функция является решение уравнения (7), то

, отсюда , (44)

где С – постоянная, и наоборот, если некоторая функция обращает в тождество (конечное) уравнение (44), то дифференцируя полученное тождество, получим . Следовательно, выражение

, (44)

где С – произвольная постоянная, суть общий интеграл уравнения (7). Его левая часть, т.е. функция , является интегралом уравнения (7) в рассматриваемом частном случае.

Некоторые элементарные уравнения в точных дифференциалах удается легко проинтегрировать приведением к виду , обходясь без квадратур и ограничиваясь лишь непосредственной группировкой их членов. Такой подход является аналогом известного в математическом анализе метода непосредственного интегрирования («внесением под знак дифференциала», только более сложным). Однако, в общем случае, уже при рассмотрении уравнения (7), возникает вопрос о самой принадлежности этого уравнения к классу уравнений в точных дифференциалах.

Пусть функции и определены и непрерывны вместе со своими первыми производными в некоторой односвязной области G. Тогда, для того чтобы уравнение (7) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие

, (45)

которое впервые получил Леонард Эйлер.

Необходимость. Если уравнение (7) в точных дифференциалах, то, согласно равенствам (43) и известной теореме из математического анализа: «результат дифференцирования не зависит от порядка, в котором производится дифференцирование, если соответствующие производные непрерывны»,

.

Достаточность. Предположим, что условие (45) выполнено. Найдем функцию , удовлетворяющую соотношениям (43). Пусть в точке функции и не обращаются одновременно в нуль. Интегрируя по переменной х в пределах от х₀ до х левое из соотношений (43) и считая у постоянной, получаем

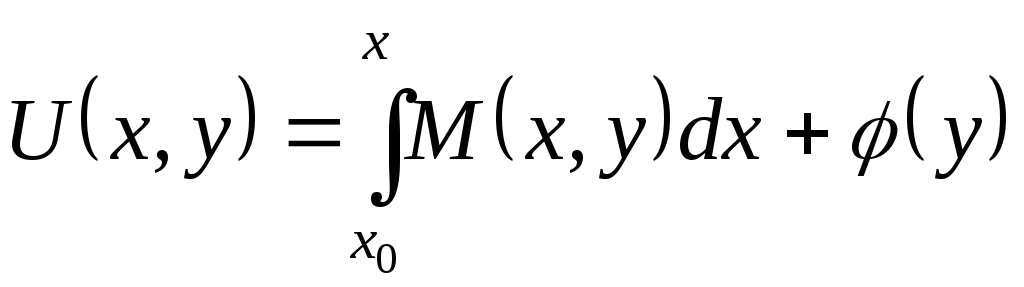, (46)

где произвольная функция. Выберем функцию так, чтобы выполнялось и второе (правое) соотношение (43). Для этого продифференцируем обе части равенства (46) по у, применяя правило дифференцирования интеграла по параметру («правило Лейбница»),

.

Заменим подынтегральную функцию, используя условие (45), и затем вычислим интеграл

.

Видно, что правая часть полученного выражения окажется в точности равной функции , если положить

, отсюда .

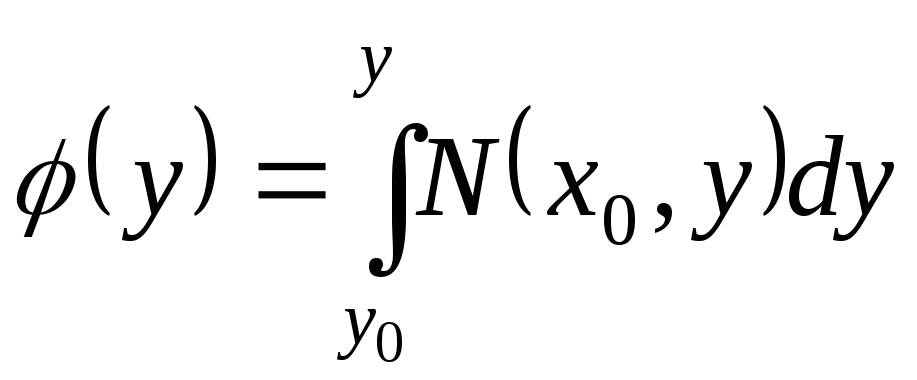Таким образом, функция найдена

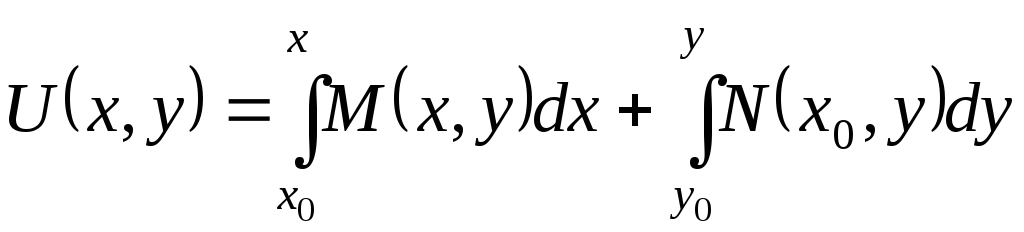
и общий интеграл (44) уравнения в полных дифференциалах (7) принимает вид

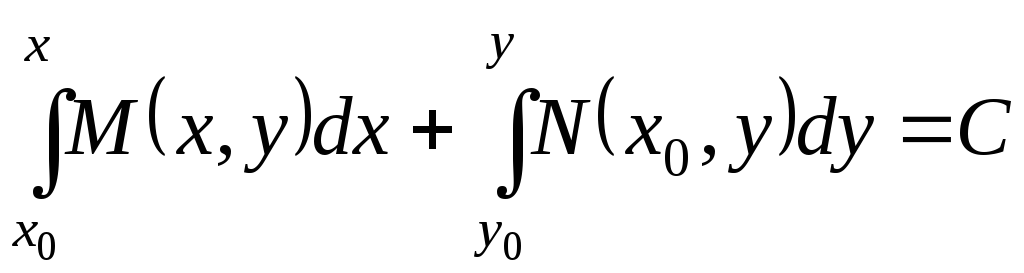, (47)

или, в силу очевидной симметрии

. (48)

Из курса математического анализа известно, что криволинейный интеграл от точного дифференциала некоторой однозначной функции по замкнутому контуру, целиком лежащему в односвязной области (т.е. стягивающемуся в точку), равен нулю. Поэтому, если выполняется условие Эйлера (5), проще проинтегрировать уравнение (7), взяв криволинейный интеграл второго типа (криволинейный интеграл по координатам) от обеих частей уравнения (7) между некоторой фиксированной точки и «подвижной» точкой по любому пути, получив таким образом решение задачи Коши в виде интеграла уравнения (7)

. (49)

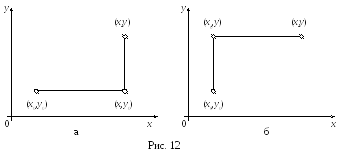
В качестве пути интегрирования удобно брать ломаную, составленную из двух звеньев, параллельным осям (рис. 12), тогда:

а) ;

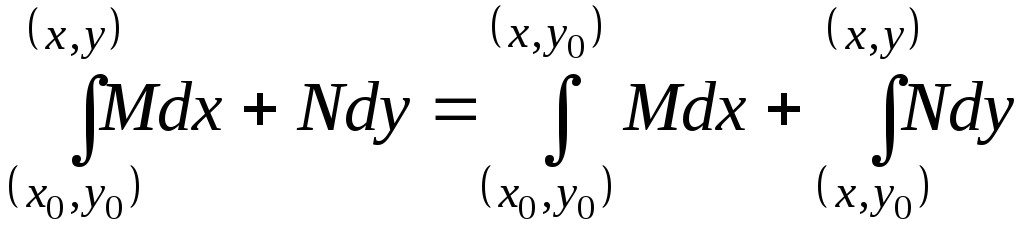б) .

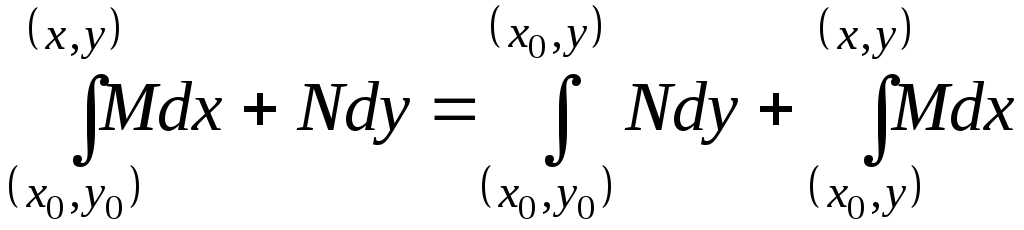Заметим, что решение задачи Коши можно получить, полагая С = 0 в равенствах (47) или (48), которое может быть представлено либо в виде в окрестности точки , согласно теории неявных функций.

Интегрирующий множитель. В некоторых случаях, когда уравнение (7) не является уравнением в полных дифференциалах, удается подобрать функцию , после умножения на которую, левая часть уравнения (7) превращается в полный дифференциал

.

Такая функция называется интегрирующим множителем.

По определению интегрирующего множителя имеем

,

или

,

откуда, деля обе части равенства на , получаем уравнение в частных производных относительно неизвестной функции

. (50)

В общем случае интегрирование этого уравнения является задачей более трудной, чем интегрирование исходного уравнения, однако в некоторых случаях подбор решения уравнения (50) сравнительно прост в осуществлении.

Считая, что интегрирующий множитель является функцией только одного аргумента (например, , , , , , и т.д.), можно уже без труда проинтегрировать уравнение (50) и указать условия, при которых интегрирующий множитель рассматриваемого вида существует. Тем самым выделяются классы уравнений, для которых интегрирующий множитель может быть найден. Рассмотрим два частных случая.

1. Если , то уравнение (50) примет вид

, . (51)

Для существования интегрирующего множителя необходимо и достаточно, чтобы правая часть уравнения (51) была функцией только х, тогда ln найдется квадратурой.

2. Аналогично, если выражение

есть функция только у, то уравнение (7) имеет интегрирующий множитель .

Если функции M и N имеют непрерывные производные в области G и по крайней мере одна из этих функций не обращается в нуль, можно доказать существование ненулевого решения уравнения в частных производных (50), или, что то же самое, существование интегрирующего множителя. Следовательно, метод интегрирующего множителя (развитый еще в работах Эйлера) можно рассматривать как общий метод интегрирования уравнений (7). Однако, ввиду трудности нахождения интегрирующего множителя этот метод применяется лишь в тех случаях, когда интегрирующий множитель очевиден.

Примеры.

30. . Это уравнение в полных дифференциалах, поскольку удовлетворяется условие (45). Группируя, находим

,

следовательно, общий интеграл данного уравнения

.

31. . Здесь не следует сокращать на , так как после сокращения левая часть перестает быть полным дифференциалом. Группируя

,

согласно формуле (44), находим общий интеграл

.

32. Найти решение задачи Коши:

, .

Здесь , , так что условие (45) выполнено, поэтому данное уравнение есть уравнение в полных дифференциалах. Замечая, что

, ,

непосредственной группировкой членов уравнения находим общий интеграл (44) данного уравнения

.

Используя начальные условия, определяем, что , следовательно, решение поставленной задачи Коши

или .

33. . Здесь

, , .

Вместо применения формул (47) или (48), на практике часто оказывается проще дифференцировать равенство (46) по у и, заменяя известной функцией , определить из полученного выражения , а затем найти квадратурой.

, ;

, .

Итак, общий интеграл .

34. Найти решение задачи Коши:

, .

Условие (45) выполнено во всей плоскости, поэтому для любой точки формулы (47) или (48) при доставляют решение задачи Коши в неявном виде

, или .

35. Найти решение задачи Коши:

, .

Здесь условие (45) выполнено во всей плоскости с выключенной точкой (0,0), т.е. в двусвязной области. Известно, что в случае многосвязной области функция (левая часть уравнения (49)) также определена во всей области , но может оказаться многозначной. В этом случае можно получать решения задачи Коши при помощи формулы (49) так же, как и при помощи формулы (47) поскольку в односвязной части любая ветвь функции удовлетворяет равенству dU = 0. Значения любой ветви функции в односвязной части области отличаются от значений другой ветви, построенной в этой области , на постоянное число. Именно поэтому следует свойство dU = 0 в случае многосвязной области , поскольку условие (45) не является достаточным в этом случае.

Применяя формулу (49) в варианте б, как показано на рис. 12, найдем интеграл рассматриваемого уравнения

Используя формулу сложения для обратных тригонометрических функций

,

из интеграла находим решение поставленной задачи Коши

, или .

36. Найти интеграл уравнения

.

Применяя формулу (49) в варианте а (рис. 12) и полагая , найдем интеграл данного уравнения.

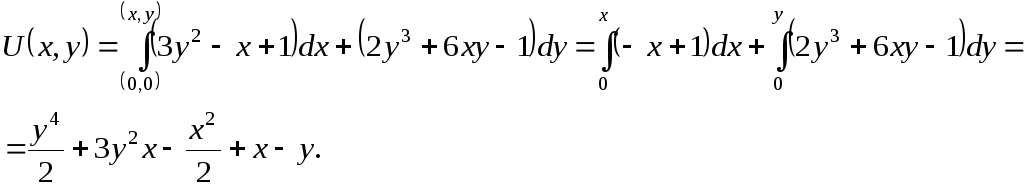
37. . Данное уравнение не является уравнением в полных дифференциалах, но, составляя уравнение для интегрирующего множителя (50), можно заметить, что выполняется частный случай 1.(51) этого уравнения.

, .

Умножением на интегрирующий множитель приводим рассматриваемое уравнение к уравнению в полных дифференциалах.

.

Показанным в примере 33 способом

, ,

, ,

находим общий интеграл данного уравнения

.

38. . Здесь для уравнения (50) выполняется частный случай 2.

, .

Соответствующее уравнение в полных дифференциалах имеет вид

.

Полагая , применим формулу (49) (рис. 12, б)

,

;

следовательно, общий интеграл рассматриваемого уравнения

.

Пусть для уравнения (7) есть какой-нибудь интересующий множитель, а есть интеграл этого уравнения. Тогда при произвольной дифференцируемой функции величина

(52)

является также интегрирующим множителем уравнения (7).

Данное утверждение воплощается на практике в виде технического приема, когда члены исследуемого уравнения разбиваются на (две) группы, для каждой из которых легко усмотреть интегрирующий множитель (и интеграл). Затем из выражений (52) для интегрирующего множителя каждой группы выбираются подходящие произвольные функции с тем, чтобы интегрирующие множители групп оказались равными (согласованными).

39. . Проинтегрируем это уравнение методом интегрирующего множителя Эйлера. Для нахождения множителя разобьем уравнение на две группы

.

Замечая, что разделение переменных сводится к умножению на некоторый интегрирующий множитель, определяем интегрирующий множитель первой скобки и интеграл

, , ;

у второй скобки очевиден интегрирующий множитель . Общее выражение интегрирующего множителя первой скобки, согласно формуле (52), имеет вид

.

Выберем теперь произвольную функцию так, чтобы множитель по переменной х совпадал бы с . Для этого достаточно положить и получить

.

Умножая исходное уравнение на , приводим его к уравнению в точных дифференциалах

,

откуда немедленно следует общий интеграл

.

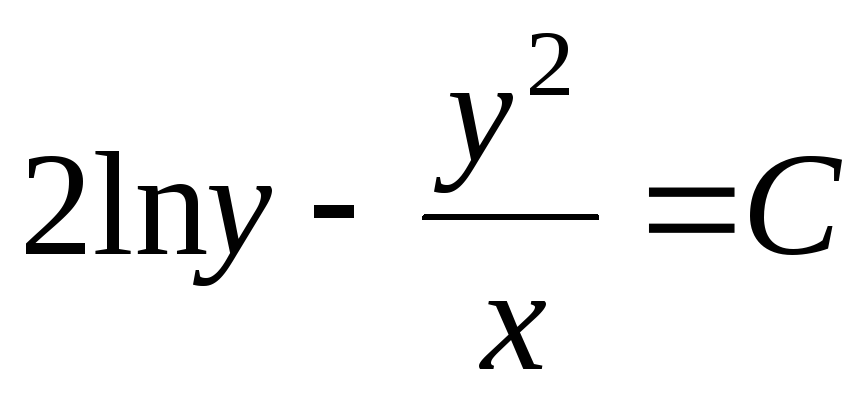40. . Группируя члены данного уравнения, можно увидеть и для отдельных групп. Однако определить сразу общий для всего уравнения интегрирующий множитель не удается, поэтому обратимся к уравнению (50).

Предположим , , , тогда

, .

Уравнение (50) принимает вид

, .

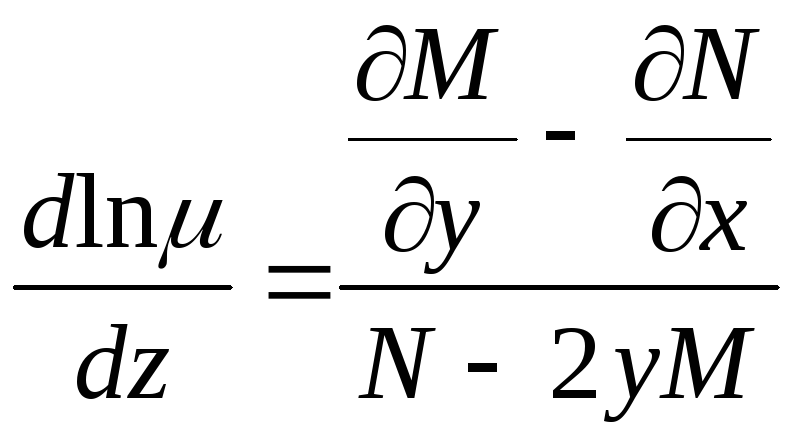Для данного уравнения , , значит

,

отсюда находим интегрирующий множитель , следовательно, данное уравнение приводится к уравнению в полных дифференциалах

,

поскольку

.

Методом, изложенным в примерах 33, 37, проинтегрируем полученное уравнение

; ;

; ;

таким образом, запишем общий интеграл исходного уравнения

.