Уравнения первого порядка, разрешенные относительно производной

Явление природы и технологические процессы существуют в некотором диапазоне изменения физических величин, поэтому все математические модели явлений и процессов наполняются конкретным содержанием, когда рассматриваются в некоторой интересующей исследователя области или заданы в ней.

Областью называется непустое множество G точек, обладающее следующими двумя свойствами: 1) каждая точка G есть внутренняя, т.е. она имеет окрестность, целиком принадлежащую G; 2) множество G связано, т.е. любые две его точки можно соединить состоящей из конечного числа звеньев ломаной, целиком лежащей внутри G.

Граничными точками области называются те точки, которые являются предельными для точек области, но не принадлежат области. Совокупность всех граничных точек называется границей области и обозначается .

Замкнутой областью или замыканием называется область вместе с ее границей, .

Геометрическая интерпретация. Понятие о задаче Коши

Пусть функция определена в некоторой области G плоскости . Уравнение

, (5)

задает в каждой точке , где существует функция , значение , т.е. угловой коэффициент касательной к интегральной кривой в этой точке. Так как с геометрической точке зрения координаты х и у равноправны, наряду с уравнением (5) рассматривать также уравнение

, , (6)

которое задает в каждой точке , где существует функция , значение , т.е. угловой коэффициент по отношению к оси Оу касательной к интегральной кривой . Очевидно, что имеющий смысл уравнения (5) и (6) эквивалентны, поскольку имеют большие интегральные кривые. Если в некоторых точках области G одно из уравнений не имеет смысла, то используется другое, заменяющее в этих точках первое уравнение. Иногда дифференциальные уравнения первого порядка можно записать в более симметричный относительно х и у форме

, (7)

где функции и определены в области G.

Если в каждой точке области G задано значение некоторой величины, то говорят, что в области G задано поле этой величины. Таким образом, дифференциальное уравнение (5) определяет поле направлений. Тройка чисел определяет направление отрезка прямой с наклоном ,проходящей через точку и называется линейным элементом. Совокупность линейных элементов образует поле направлений. Дифференциальное уравнение тем самым отождествляется со своим полем направлений.

Задача интегрирования в геометрической интерпретации ставится так: в области G найти все линии, имеющие в каждой точке направление, заданное уравнениями (5), (6). Эта математически строгая формулировка для практических целей может быть истолкована конструктивнее: в области Gнайти некоторые кривые такие, чтобы касательные к ним в каждой точке имели направления, совпадающие с направлениями в этих точках. Эти кривые (линии) называются интегральными кривыми (линиями) рассматриваемого уравнения.

Задача построения интегральной кривой в грубом, нулевом приближении часто решается введением изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и то же направление. Семейство изоклин дифференциального уравнения (5) определяется уравнением

, , , (8)

где k – параметр. Придавая параметру k близкие числовые значения, можно получить достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые (геометрический образ общего интеграла) дифференциального уравнения (5) в рассматриваемой области G.

Нулевая изоклина дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых, она делит область G на части, в каждой из которых сохраняет постоянный знак. Интегральные кривые , пересекая нулевую изоклину, переходят из области возрастания функции в область убывания или наоборот. Для лучшего качества построения интегральных кривых в сложных случаях находят геометрическое место точек перегиба, в которых . Дифференцированием по х уравнения (5), с использованием самого уравнения (5), находят

и приравнивают ее к нулю. Линия, определяемая уравнением

, (9)

и есть возможное геометрическое место точек перегиба; она разбивает область G на две части, в одной из которых , и, следовательно, интегральные кривые выпуклы вверх, а в другой , и значит, интегральные кривые вогнуты вверх.

Примеры.

7

Рис. 1

. . В данном случае изоклинами являются (рис. 1) полупрямые , в которых угловой коэффициент касательной к искомой интегральной кривой. Интегральными кривыми будут полупрямые . Здесь начало координат (0,0) – особая точка уравнения, в ней не определено поле направления, поскольку правая часть уравнения обращается в неопределенность .

8. . Уравнение изоклин получим, полагая (рис. 2) или , следовательно, в данном случае изоклинами являются окружности с центром в начале координат; угловой коэффициент касательной к искомым интегральным кривым равен радиусу этих окружностей. Задавая масштаб, дадим постоянной k некоторые определенные значения, например, , , 1, , 3. Тогда, согласно формуле

(8), углы наклона линейных элементов на этих окружностях будут выражены (в градусах) соответственно , 30, 45, 60, . Общее решение данного уравнения в окрестности начала координат схематично показано на рис. 2.

9

у

х

1

-1

Рис. 3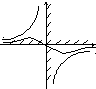

. . Изоклинами этого уравнения являются гиперболы или , при параметре k принимающем положительные и отрицательные значения. При k=0 получаем нулевую изоклину; k=1 гипербола распадается на пару прямых х=0 и у=0. При переходе через нулевую изоклину величина меняет свой знак, как показано на рис. 3. Применяя формулу (9), находим линию точки перегиба интегральных кривых

или ,

отсюда .

При переходе через эту линию интегральные кривые переходят от выпуклости к вогнутости , как показано на рис. 3, где линия точек перегиба выделена жирно. Рассматривая разность между этой линией и нулевой изоклиной

, ,

видим, что она положительна в правой полуплоскости и отрицательна в левой. Следовательно, линия точек перегиба проходит под нулевой изоклиной, при , и над нулевой изоклиной, если , и эти линии никогда не пересекаются. Однако, решая совместное уравнение

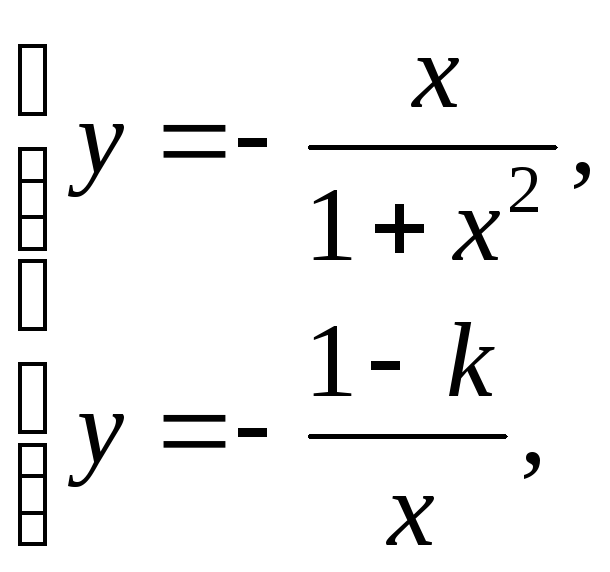
убеждаемся, что при существует их решение, совпадающее с координатами точки касания гиперболы и прямой с угловым коэффициентом равным k. Этих сведений достаточно, чтобы сделать набросок расположения интегральных кривых (рис. 4).

Трудами многих ученых в течение XVIII века был накоплен большой опыт по составлению дифференциальных уравнений и нахождению их общих решений или общих интегралов в различных приложениях. Обычный подход заключался в предварительном разыскании общих интегралов, содержащих неизвестные функции и константы, и лишь затем в подборе констант и определении неизвестных функций. О. Коши (1789–1857) в своих работах отмечал, что на практике наибольший интерес представляют частные решения, в которых произвольные постоянные определены исходя из некоторых стандартных условий, названных им начальными условиями. Начальными они названы потому, что изначально фиксируется значение независимой переменной х и выбираются (считающимися известными из практических или иных соображений) значения неизвестной функции и ее производных до -го порядка, если рассматривается уравнение (1). Для дифференциального уравнения первого порядка начальная задача ставится так.

Задача Коши. Пусть функция определена и непрерывна по переменным х, у и имеет ограниченную частную производную по переменной у в замкнутой области , например (рис. 5), .

Найти функцию , удовлетворяющую уравнению

(5)

и условию , . (10)

поставленная задача Коши всегда имеет единственное решение, которое может быть найдено, например, методом последовательных приближений Пикара (1856–1941). Заслуга Коши заключается в том, что он доказал существование и единственность начальной задачи не только для уравнения (5), но и для упоминавшейся выше нормальной системы и тем самым резко упростил нахождение нужных на практике решений.

С геометрической точки зрения решить задачу Коши значит найти интегральную кривую , проходящую через заданную внутри области G точку .

Условия (10) называются начальными условиями решения , а числа и – начальными данными этого решения. Задача нахождения решения уравнения (5), удовлетворяющего заданным начальным условиям (10) называется задачей Коши. Вообще решение задачи Коши для уравнения (5) в любой из форм (6),

(7) его записи ищут в том виде, в каком это оказывается наиболее удобно, т.е. в виде , , или в параметрической форме , .

Решение задачи коши стараются найти в элементарных функциях или в квадратурах от элементарных функций. В тех случаях, когда это не удается, приходится прибегать к приближенным методам интегрирования, в основе которых лежит метод ломаных Эйлера, предложенный знаменитым математиком членом Петербургской академии наук, Леонардом Эйлером (1707–1783). Более того, метод Эйлера лежит в основе теорем о существовании и единственности поставленной задачи (5), (10) Коши, поэтому рассмотрим его подробнее.

Как известно, уравнение (5) с заданной в области G функции определяет в G после направлений, которые должны иметь интегральные линии.

Возьмем в области G точку . Ей будет соответствовать проходящая через эту точку прямая с угловым коэффициентом . На этой прямой в области G возьмем точку (на рис. 5 обозначена цифрой 1). Через точку проведем прямую с угловым коэффициентом , на которой отметим принадлежащую G точку (на рис. 5 обозначена цифрой 2). Затем на прямой, соответствующей точке , отмечаем точку и т.д. Пусть при этом такое построение можно выполнять и в сторону убывающих значений х. Получим ломаные линии, которые называют ломаными Эйлера. Естественно ожидать, что каждая из ломаных Эйлера с достаточно короткими звеньями дает некоторое представление об интегральной кривой, проходящей через точку , и что при уменьшении длин звеньев ломаные Эйлера будут приближаться к этой интегральной кривой. Для численных расчетов интервал непрерывного изменения аргумента заменяем дискретным множеством точек , , где h – малое число, называемое параметром или шагом сетки . Если , то сетка называется равномерной. Заменяя производную в уравнении (5) отношением конечных приращений

,

с учетом правой части уравнения (5) и условий (10) имеем законченный вычислительный алгоритм интегрирования

, , .

Погрешность этого метода на всем интервале при малом параметре h порядка h, поэтому целесообразно для повышения точности уменьшать шаг.