
- •Обыкновенные дифференциальные уравнения Общие понятия
- •Уравнения первого порядка, разрешенные относительно производной
- •Геометрическая интерпретация. Понятие о задаче Коши
- •Уравнение, не содержащее искомой функции
- •Уравнение, не содержащее независимой переменной
- •Уравнение с разделяющимися переменными
- •Однородное уравнение
- •Уравнение в полных дифференциалах
- •Линейное уравнение
- •Уравнение Бернулли
- •Уравнения первого порядка, не разрешенные относительно производной Основные понятия и определения
Уравнение Бернулли
Дифференциальное уравнение Бернулли имеет вид
![]() ,
(64)
,
(64)
где заданные
функции
![]() и
и
![]() определены и непрерывны в интервале
определены и непрерывны в интервале
![]() ,
а n – вещественное
число, отличное от 0 и 1 (так как при
,
а n – вещественное
число, отличное от 0 и 1 (так как при
![]() или
или
![]() уравнение Бернулли обращается в линейное
дифференциальное уравнение).
уравнение Бернулли обращается в линейное
дифференциальное уравнение).
Уравнение Бернулли (64) приводится к линейному введением новой переменной
![]() ,
,
![]() .
(65)
.
(65)
Для новой искомой функции и получаем уравнение
![]() . (66)
. (66)
Согласно формуле (59), общее решение уравнения (66)
![]() ,
(67)
,
(67)
следовательно, общее решение уравнения Бернулли
 . (68)
. (68)
Из уравнения (64)
видно, что при
![]() существует решение
существует решение
![]() этого уравнения.
этого уравнения.
Если
![]() ,
то прямая
,
то прямая
![]() является асимптотой всех интегральных
кривых уравнения Бернулли, а, значит,
частным решением этого уравнения,
которое получается из формулы (68) при
является асимптотой всех интегральных
кривых уравнения Бернулли, а, значит,
частным решением этого уравнения,
которое получается из формулы (68) при
![]() .
(В формуле (68) можно положить
.
(В формуле (68) можно положить
![]() и, заново переписав формулу, получить
решение
и, заново переписав формулу, получить
решение
![]() при
при
![]() ).
).
Если
![]() ,
то
,
то
![]() является особым решением уравнения
Бернулли, оно не может быть получено из
общего решения (68) ни при каком значении
постоянной интегрирования С.
является особым решением уравнения
Бернулли, оно не может быть получено из
общего решения (68) ни при каком значении
постоянной интегрирования С.
Из вышеизложенного следует, что вопросы, связанные с интегрированием и изучением поведения решений уравнения Бернулли, сводятся к аналогичным вопросам для линейного уравнения. Однако, классически уравнение (64) интегрируется непосредственно применением мультипликативной подстановки Бернулли (55) (или методом Лагранжа) без предварительного сведения его к линейному.
Примеры.
46.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() .
.
Подстановкой (55) получаем вспомогательное уравнение
![]() ,
,
из которого определяем первую искомую функцию и
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Подставляем функцию и снова во вспомогательное уравнение и находим вторую искомую функцию v
![]() ,
,
![]() ;
;
![]() .
.
Согласно подстановке (55), общее решение данного уравнения запишем в двух видах:
а)
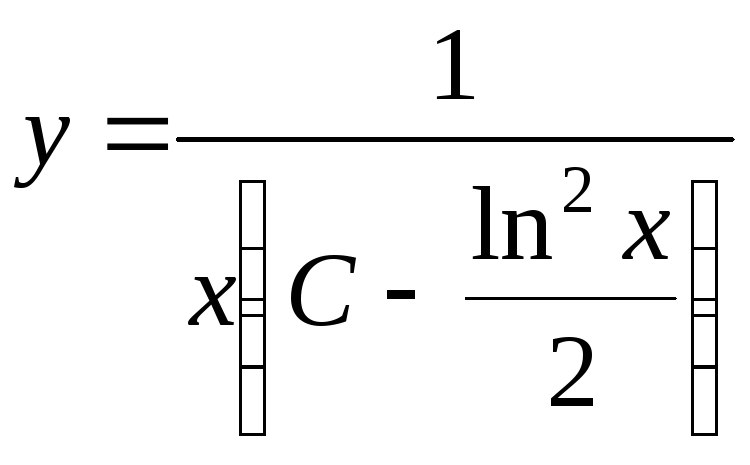 ;
б)
;
б)
 ,
,
![]() .
.
Отсюда решения поставленных задач Коши:
а)
![]() ;
б)
;
б)
![]() .
.
47.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() .
.
Решаем соответствующее линейное однородное уравнение
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Варьируя по Лагранжу
постоянную интегрирования
![]() ,
находим общее решение данного уравнения
,
находим общее решение данного уравнения
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
окончательно,
![]() .
.
В окрестности точки (1,1) выполняются условия существования и единственности задачи Коши для данного уравнения, поэтому из общего решения, с использованием начальных данных, находим решение поставленной задачи Коши в варианте а)
![]() ,
,
![]() ;
а)
;
а)
![]() .
.
Действуя формально, нетрудно получить решение задачи Коши в варианте б)
![]() ,
,
![]() ;
б)
;
б)
![]() ;
;
![]() ,
,
однако, это решение
не является единственным, поскольку
через точку (1,0) проходит еще очевидное
решение
![]() ,
которое является особым решением
данного уравнения. Линия
,
которое является особым решением
данного уравнения. Линия
![]() является с одной стороны интегральной
кривой данного уравнения, а с другой
– геометрическим местом точек, в каждой
из которых нарушается свойство
единственности (проще говоря,
геометрическим местом тех точек, где
является с одной стороны интегральной
кривой данного уравнения, а с другой
– геометрическим местом точек, в каждой
из которых нарушается свойство
единственности (проще говоря,
геометрическим местом тех точек, где
![]() бесконечна).
бесконечна).
Решения поставленной задачи Коши в варианте б) для данного уравнения нет.
48.
![]() .
.
Методом Бернулли,
полагая
![]() ,
найдем общий интеграл данного уравнения
,
найдем общий интеграл данного уравнения
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Особых решений
нет. Линия
![]() ,
на которой нарушается свойство
единственности, не является решением
данного уравнения.
,
на которой нарушается свойство
единственности, не является решением
данного уравнения.
49.
![]() .
Это нелинейное уравнение. Полагая
.
Это нелинейное уравнение. Полагая
![]() ,
приводим его к классическому виду (64)
уравнения Бернулли
,
приводим его к классическому виду (64)
уравнения Бернулли
![]() .
.
Методом Лагранжа находим общий интеграл уравнения Бернулли.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]()
(здесь применялось интегрирование по частям);
![]() .
.
Возвращаясь к старым переменным, запишем общий интеграл исходного уравнения
![]() .
.
50.
![]() .
Данное дифференциальное уравнение
является нелинейным. Элементарными
преобразованиями оно приводится к
уравнению Бернулли, если рассматривать
переменную х кА функцию от у.
.
Данное дифференциальное уравнение
является нелинейным. Элементарными
преобразованиями оно приводится к
уравнению Бернулли, если рассматривать
переменную х кА функцию от у.
![]() .
.
Будем искать общее
решение этого уравнения методом Бернулли
подстановкой
![]()
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
далее, квадратурой, с интегрированием по частям, находим
![]() .
.
Зная функции u, v, после некоторых преобразований, запишем общий интеграл данного уравнения в виде
![]() .
.
