Подставляем полученное соотношение в исходное уравнение

Из этого уравнения определим переменную функцию С₁(х):

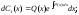
Интегрируя, получаем:

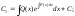
Подставляя это значение в исходное уравнение, получаем:

.

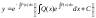Таким образом, мы получили результат,

33.Уравнение Бернулли.

Определение. Уравнением Бернулли называется уравнение вида

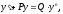где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.

Для решения уравнения Бернулли применяют подстановку 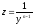, с помощью которой, уравнение Бернулли приводится к линейному.

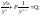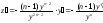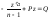
Для этого разделим исходное уравнение на yⁿ. Применим подстановку, учтя, что . 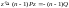Т.е. получилось линейное уравнение относительно неизвестной функции z. Решение этого уравнения будем искать в виде:

Пример. Решить уравнение

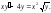
Разделим обе части уравнения на

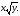
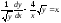
Полагаем

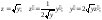
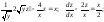
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:

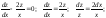
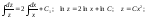
Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:

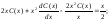
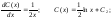
Получаем:

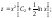
Применяя обратную подстановку, получаем окончательный ответ:

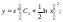
Дифференциальные уравнения высших порядков.

Определение. ДУ порядка n называется уравнение вида: 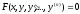В некоторых случаях это уравнение можно разрешить относительно y⁽ⁿ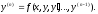⁾: Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений. Определение. Решение 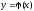удовлетворяет начальным условиям 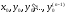, если Определение. Нахождение решения уравнения 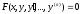, удовлетворяющего начальным условиям 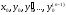, называется решением задачи Коши. Теорема Коши. Если функция (n-1) –й переменных вида 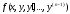в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по 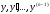, то какова бы не была точка (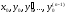) в этой области, существует единственное решение 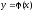уравнения 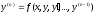, определенного в некотором интервале, содержащем точку х₀, удовлетворяющее начальным условиям .

ДУ высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.

Уравнения вида y⁽ⁿ⁾ = f(x). Если f(x) – ф-я непрерывная на некотором промежутке a < x < b, то реш может быть найдено последовательным интегрированием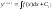

………………………………

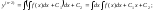
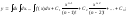
34Уравнения, не содержащие явно искомой функциии ее производных до порядка k – 1 включительно. Это уравнения вида: 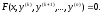В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной: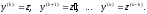

Тогда получаем: 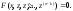Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением: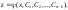Делая обратную подстановку, имеем:Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ:

34.Ур-я, не содержащие явно независимой переменной.

Это уравнения вида

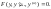
Порядок таких уравнений может быть понижен на единицу с помощью замены переменных

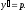
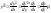
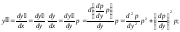и т.д.

Подставляя эти значения в исходное дифференциальное уравнение, получаем:

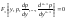
Если это уравнение проинтегрировать, и - совокупность его решений, то для решения данного дифференциального уравнения остается решить уравнение первого порядка: