
- •Часть 1
- •3.1 Появление определителей в теории слау
- •3.2 Отображения
- •3.3 Перестановки n-ой степени
- •3.4 Четные и нечетные перестановки
- •3.5 Суммирование по множеству
- •3.6 Определитель n-го порядка
- •3.7 Свойства определителя
- •3.8 Теорема Лапласа
- •3.9 Разложение определителя по элементам строки или столбца
- •Определитель произведения матриц
- •Формула обратной матрицы
- •Теорема Крамера
- •Упражнения
- •Историческая справка
- •Литература Основная литература.
- •Задачники и дополнительные методические материалы.
Упражнения
-
Какие из приведенных ниже таблиц являются перестановками?
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
,![]()
![]()
е)
![]() ,
ж)
,
ж)
![]() ,
з)
,
з)![]()
![]()
![]() ,
,
и)
![]()
![]() .
.
-
Все перестановки из упражнения 1 привести к каноническому виду и найти числа их инверсий.
-
Для следующих перестановок найти им обратные перестановки:
а)
![]()
![]() ,
б)
,
б)
![]()
![]() ,
в)
,
в)![]()
![]() ,
,
г)
![]()
![]() ,
д)
,
д)![]()
![]() .
.
-
Найти произведения следующих перестановок:
а)![]()
![]() ,
б)
,
б)
![]()
![]() ,
,
в)![]()
![]() ,
г)
,
г)![]()
![]() .
.
-
Следующие перестановки разложить в произведения: а) независимых циклов, б) транспозиций, в) простых транспозиций;– и указать их четность:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)![]()
![]() ,
,![]() г)
г)![]()
![]() ,
,
д)
![]()
![]() ,
е)
,
е)
![]() ,
ж)
,
ж)
![]() ,
,
з)
![]() ,
и)
,
и)
![]() .
.
-
Какое наибольшее число инверсий может иметь перестановка порядка: а) 2, б) 4, в) 7, г) 15, д) n ?
-
С каким знаком в определители соответствующих порядков будут входить произведения: а) a21a13a32, б) а42а11а23а34, в) а15а43а24а51а32, г) а36а57а24а15а72а63а41 ?
-
Какие значения должны принимать m и k с тем, чтобы произведение
а14а25а3mа47а5kа62а73 входило в определитель 7-го порядка: а) со своим знаком, б) с противоположным знаком?
-
Вычислить следующие определители 2-го и 3-го порядков, используя их определение:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() ,
,
ж)
![]() ,
з)
,
з)
 ,
и)
,
и)
![]() ,
к)
,
к)
 ,
,
л)
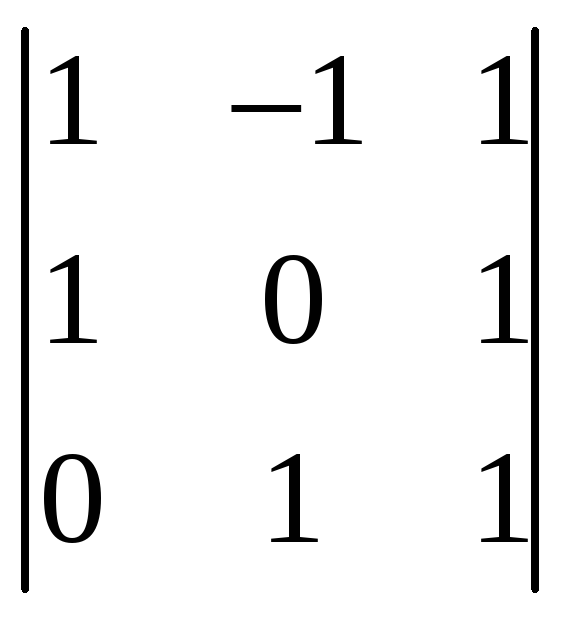 ,
м)
,
м)
 ,
н)
,
н)
 ,
о)
,
о)
 ,
п)
,
п)
 .
.
Как уже отмечалось
выше в пункте 3.6, в общем случае
использование формулы (3.18) для вычисления
определителей малоэффективно. Один из
основных способов вычисления определителей
связан с предложением 3.15 и опирается
на приемы, используемые в методе Гаусса
для решения систем линейных алгебраических
уравнений ([1],[14],[24],[25],[33],[34]). Выбирая в
определителе подходящий ведущий элемент,
с помощью строчных элементарных
преобразований приводим определитель
![]() к виду (3.30), учитывая при этом предложения
3.8 и 3.12. Использование после этого
предложения 3.15 приводит к определителю
порядка на единицу меньше. Повторяя
этот процесс нужное число раз, приходим
к определителю порядка 2, который
вычисляется по формуле (3.18).
к виду (3.30), учитывая при этом предложения
3.8 и 3.12. Использование после этого
предложения 3.15 приводит к определителю
порядка на единицу меньше. Повторяя
этот процесс нужное число раз, приходим
к определителю порядка 2, который
вычисляется по формуле (3.18).
Пример 14. Продемонстрируем этот способ на следующем примере.


 .
►
.
►
-
Вычислить следующие определители:
а)
 ,
б)
,
б)
 ,
в)
,
в)
 ,
г)
,
г)
 .
.
При вычислении
определителей полезно также использовать
элементарные преобразования
![]() и
и
![]() .
При этом в силу Предложения 3.8 необходимо
каждый раз умножать определитель на
.
При этом в силу Предложения 3.8 необходимо
каждый раз умножать определитель на
![]() для того, чтобы не изменить его значения.
для того, чтобы не изменить его значения.
Пример 15. Вычислим следующий определитель

 =
=

=
 =
=![]()
-
Вычислить следующие определители:
а)
 ,
б)
,
б)
 ,
в)
,
в)
 ,
,
г)
 ,
д)
,
д)
 ,
е)
,
е)
 .
.
Прежде чем начинать вычислять определитель, следует, учитывая его особенности, провести ряд вспомогательных преобразований, упрощающих задачу. Типичным примером являются определители, у которых сумма всех элементов, стоящих в каждой его строке (в каждом его столбце), одинакова.
Пример 16. Вычислить

◄ Каждая строка
определителя, начиная со второй, получена
циклическим сдвигом предыдущей строки
на один элемент вправо. Поэтому сумма
элементов каждой строки одинакова и
равна
![]() Прибавляя к первому столбцу все остальные
столбцы, получаем
Прибавляя к первому столбцу все остальные
столбцы, получаем


Далее заметим, что
сумма первого и третьего столбцов имеет
одинаковые с точностью до знака элементы.
Проводя преобразование
![]() ,
получаем
,
получаем


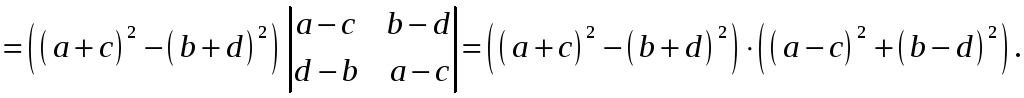 ►
►
12. Вычислить следующие определители:
а)
 ,
,
 ,
,
 ,
,

 .
.
Напомним, что определитель матрицы треугольного вида равен произведению диагональных элементов.
13.Следующие определители вычислить методом приведения к треугольному виду:







Определители, имеющие большое количество нулевых элементов, часто удобно вычислять, применяя разложение его по столбцу или строке.
Пример 17. Вычислить следующий определитель, где значок « / » означает «произвольный элемент»

◄ Решение этого примера проведем двумя способами.
Первый способ – разложение определителя по столбцу:

![]()
Второй способ – по определению.
Данный определитель содержит 24 члена, один из которых равен
![]() где
где

Легко заметить, что остальные члены определителя равны нулю, так каждый из них содержит по крайней мере один из нулевых сомножителей. Поэтому
![]() ►
►
14. Следующие определители вычислить методом разложения по строке или столбцу.


Описанные выше методы вычисления определителей малых порядков (приведение к треугольному виду, разложение по строке или столбцу, использование основного определения) применимы и для вычисления определителей произвольного порядка n. Получаемый при этом ответ зависит от n и, следовательно, представляет собой формулу вычисляемого определителя. Прежде чем выводить искомую формулу определителя следует выяснить каков порядок определителя, а после получения его формулы в целях контроля за правильностью вычислений следует проверить её верность для малых размеров.
Пример 18. Найти формулу для вычисления определителя
 .
.
◄ Данный определитель
имеет порядок n.
Будем его вычислять по второму варианту
решения примера 17. Из
![]() членов данного определителя
членов данного определителя
![]() член равен
нулю, так как содержит по меньшей мере
один нулевой сомножитель. Поэтому
член равен
нулю, так как содержит по меньшей мере
один нулевой сомножитель. Поэтому
![]() где
где


Следовательно,
![]() ► (3.44)
► (3.44)
Замечание 3. Обращаем внимание на то, что по формуле (3.44) также вычисляются треугольные определители порядка n

Пример 19. Вычислить определитель

◄ Считая, что определитель имеет порядок n, прибавим к его первому столбцу все остальные столбцы, а после этого вычтем первую строку из всех остальных строк. Получаем, что

 ►
►
Для нахождения формулы определителя порядка n можно применять метод полной математической индукции.
Пример 20. Найти формулу вычисления определителя

◄ Вначале
сформулируем гипотезу для формулы
определителя
![]() и для этого вычислим определители
и для этого вычислим определители
![]()
![]()
представляя последнюю строку в виде суммы двух строк, получаем, что





В результате мы можем сформулировать гипотезу о том, что
 (3.45)
(3.45)
Остается совершить индукционный переход. Пусть формула (3.45) верна. Тогда



Откуда
следует, что формула (3.45) верна для всех
![]() ►
►
Пример 21. Вычислить определитель порядка 2n

◄ Расписав определитель более подробно, получаем, что



![]() ►
►
15. Вычислить определители:



16. Вывести формулы для вычисления определителей:



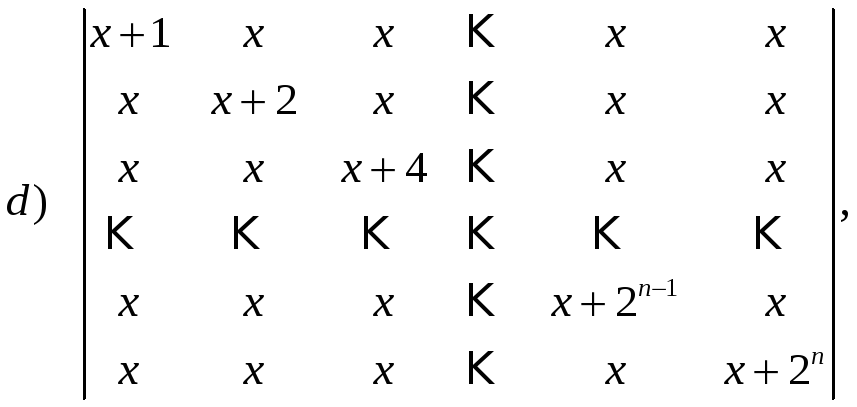


Другие способы вычисления определителей произвольного порядка читатель может найти в задачнике [20].
