
- •Задачи для самостоятельного решения
- •9. Определенный интеграл
- •10. Применение определенных интегралов. Несобственные интегралы
- •Объем тела вращения
- •Длина дуги плоской кривой
- •Несобственные интегралы с бесконечными пределами интегрирования
- •Несобственные интегралы от неограниченных функций
- •Задачи для самостоятельного решения
- •10. Применение определенных интегралов. Несобственные интегралы
- •11. Дифференциальные уравнения
- •Дифференциальные уравнения первого порядка. Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод подстановки (метод Бернулли)
- •Задачи для самостоятельного решения
- •11. Дифференциальные уравнения
- •12. Числовые ряды
- •Ряды с положительными членами. Признаки сходимости
- •Знакочередующиеся ряды. Признак сходимости Лейбница
- •Знакопеременные ряды
- •Задачи для самостоятельного решения
- •12. Числовые ряды
- •13. Степенные ряды
- •Содержание
- •Минченков Юрий Владимирович высшая математика Сборник задач по математическому анализу
- •220086, Минск, ул. Славинского, 1, корп. 3.
Определение.
Если существует
конечный предел интегральной суммы (1)
и он не зависит ни от способа разбиения
отрезка
![]() на частичные отрезки, ни от выбора точек
на частичные отрезки, ни от выбора точек
![]() в них, то этот предел называется
определенным интегралом от функции
в них, то этот предел называется
определенным интегралом от функции
![]() на отрезке
на отрезке
![]() и обозначается
и обозначается
![]() .
Таким образом,
.
Таким образом,
![]() .
.
В этом случае
функция
![]() называется интегрируемой на
называется интегрируемой на
![]() .
Числа а и
b
называются соответственно нижним и
верхним пределами интегрирования,
.
Числа а и
b
называются соответственно нижним и
верхним пределами интегрирования,
![]() – подынтегральной функцией,
– подынтегральной функцией,
![]() – подынтег-ральным выражением,
– подынтег-ральным выражением,
![]() – переменной интегрирования; отрезок
– переменной интегрирования; отрезок
![]() называется
промежутком интегрирования.
называется
промежутком интегрирования.
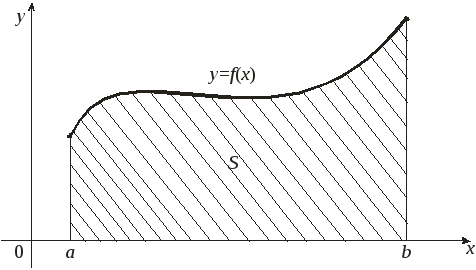
Определенный
интеграл
![]() от неотрицательной функции
от неотрицательной функции
![]() с геометрической точки зрения численно
равен площади криволинейной трапеции,
ограниченной сверху графиком функции
с геометрической точки зрения численно
равен площади криволинейной трапеции,
ограниченной сверху графиком функции
![]() ,
слева и справа – отрезками прямых
,
слева и справа – отрезками прямых
![]() и
и
![]() ,
снизу – отрезком
,
снизу – отрезком
![]() оси Ох.
оси Ох.
Теорема
1. Если
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и
и
![]() – какая-либо
ее первообразная на этом отрезке, то
справедлива следующая формула:
– какая-либо
ее первообразная на этом отрезке, то
справедлива следующая формула:
![]() ,
(2)
,
(2)
которая называется
формулой
Ньютона–Лейбница.
Разность
![]() принято записывать следующим образом:
принято записывать следующим образом:
![]() ,
,
где символ![]() называется знаком двойной подстановки.
называется знаком двойной подстановки.
Таким образом, формулу (2) можно записать в виде:
![]() .
.
Пример 1.
Вычислить интеграл
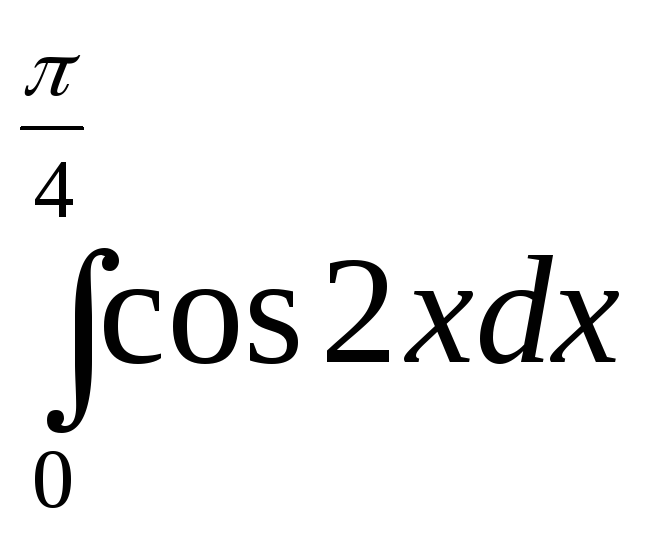 .
.
Решение. По формуле Ньютона-Лейбница имеем:
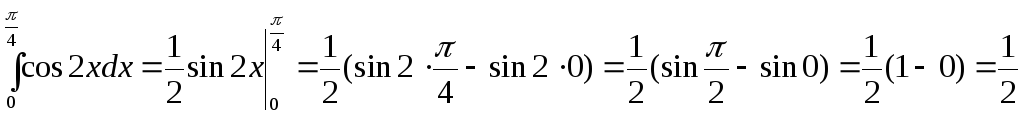 .
.
Теорема
2. Пусть
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() .
Тогда, если:
1) функция
.
Тогда, если:
1) функция
![]() и ее производная
и ее производная
![]() непрерывны при
непрерывны при
![]() ;
2) множеством
значений функции
;
2) множеством
значений функции
![]() при
при
![]() является отрезок
является отрезок
![]() ;
3)
;
3)
![]() ,
,
![]() ,
то справедлива
формула
,
то справедлива
формула
![]() ,
(3)
,
(3)
которая называется формулой замены переменной в определенном интеграле.
Пример 2.
Вычислить интеграл
![]() .
.
Решение.
Введем новую переменную по формуле
![]() .
Определим
.
Определим
![]() и
и
![]() .
Возведя в квадрат обе части равенства
.
Возведя в квадрат обе части равенства
![]() ,
получим
,
получим
![]() ,
откуда
,
откуда
![]()
![]() .
Находим новые пределы интегрирования.
Для этого в формулу
.
Находим новые пределы интегрирования.
Для этого в формулу![]() подставим старые пределы
подставим старые пределы
![]() и
и
![]() .
Получим:
.
Получим:
![]() ,
откуда
,
откуда
![]() и, следовательно,
и, следовательно,
![]() ;
;
![]() ,
откуда
,
откуда
![]() и, следовательно,
и, следовательно,
![]() .
Таким образом:
.
Таким образом:
![]()
![]() .
.
Теорема
3. Пусть
функции
![]() и
и
![]() имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке
![]() ,
тогда имеет место следующая формула
интегрирования по частям:
,
тогда имеет место следующая формула
интегрирования по частям:
![]() .
(4)
.
(4)
Пример 3.
Вычислить
![]() .
.
Решение.
Положим
![]() ,
отсюда
,
отсюда
![]() .
По формуле (4) находим
.
По формуле (4) находим
![]()
![]() .
.
Пример 4.
Вычислить
![]() .
.
Решение.
Пусть
![]() ,
тогда
,
тогда
![]() .
Применяя формулу интегрирования по
частям, получаем
.
Применяя формулу интегрирования по
частям, получаем
![]()
![]() .
.
Задачи для самостоятельного решения
9. Определенный интеграл
1. Вычислить определенные интегралы:
a)
![]() ;
б)
;
б)
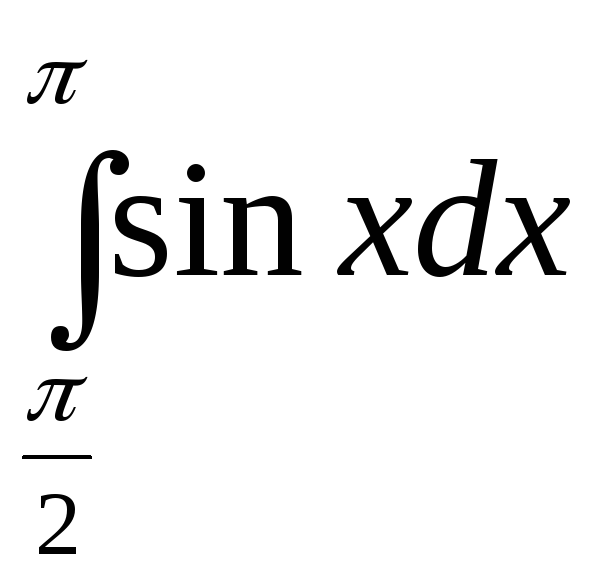 ;
в)
;
в)
![]() ;
г)
;
г)
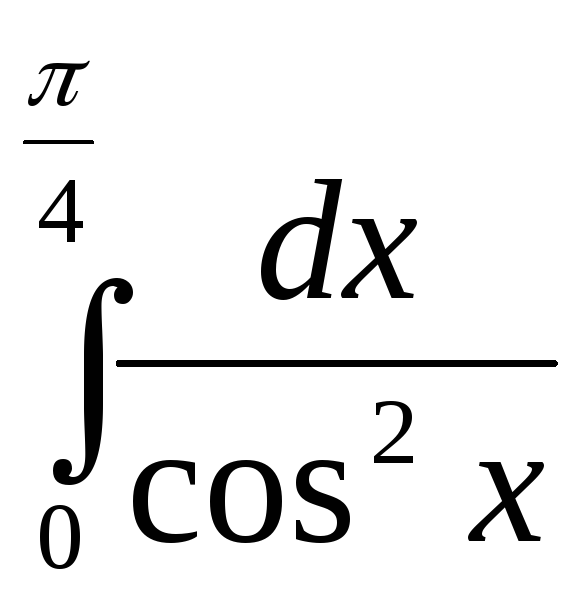 ;
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
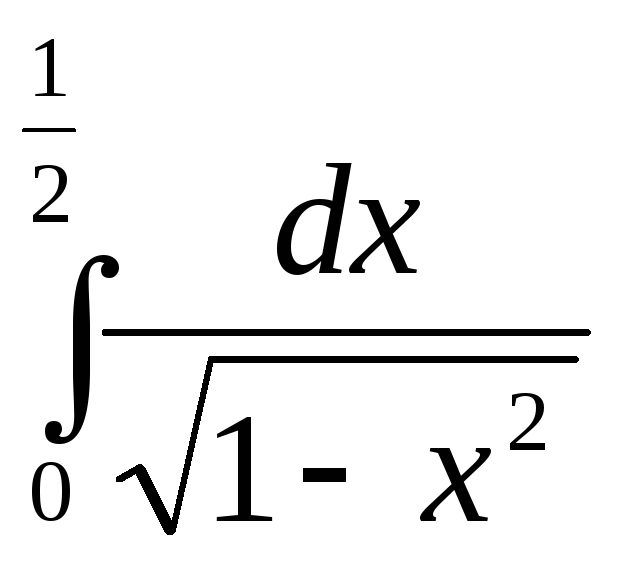 ;
з)
;
з)
![]() .
.
2. Применяя метод замены переменной, вычислить следующие интегралы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
3. Применяя метод интегрирования по частям, вычислить следующие интегралы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
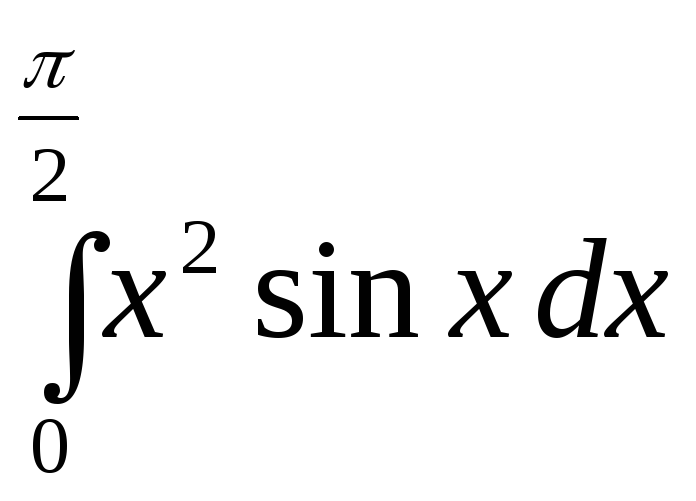 ;
е)
;
е)
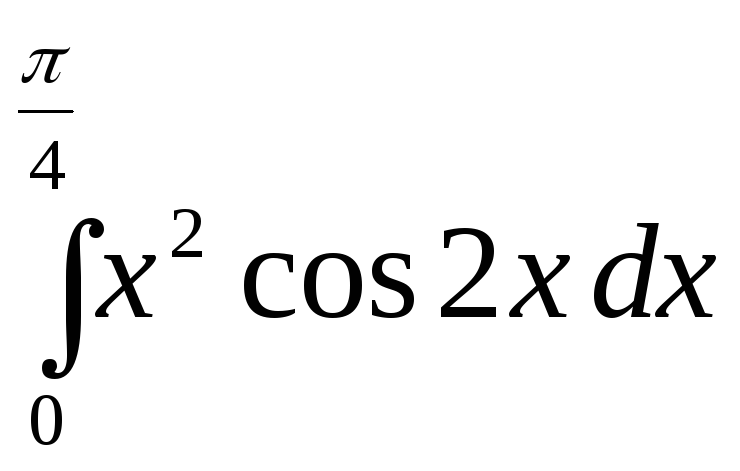 .
.
10. Применение определенных интегралов. Несобственные интегралы
Пусть криволинейная
трапеция ограничена сверху и снизу
графиками непрерывных на отрезке
![]() функций
функций
![]() и
и
![]() ,
а слева и справа
– прямыми
,
а слева и справа
– прямыми
![]() и
и
![]() .
Тогда ее площадь вычисляется по формуле
.
Тогда ее площадь вычисляется по формуле
![]() .
(1)
.
(1)
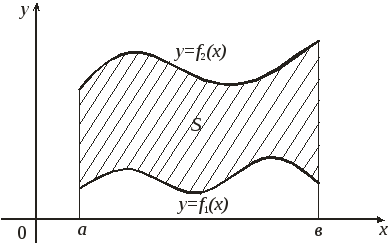
Пример 1.
Найти площадь фигуры, ограниченной
линиями
![]() и
и
![]() .
.
Решение.
Данная фигура изображена на рисунке.
Площадь ее вычислим по формуле (1). Решая
систему уравнений
![]() находим
находим
![]() ,
,
![]() ,
следовательно,
,
следовательно,
![]() ,
,
![]() .
На отрезке
.
На отрезке
![]() имеем
имеем
![]() .
Значит, в формуле (1)
.
Значит, в формуле (1)
![]() = x,
а
= x,
а
![]() =
=
![]() .
Получим:
.
Получим:
![]()
![]()
![]() (кв. ед.).
(кв. ед.).

Объем тела вращения
Пусть криволинейная
трапеция, ограниченная графиком
непрерывной на отрезке
![]() функции
функции
![]() ,
осью
,
осью
![]() ,
прямыми
,
прямыми
![]() и
и
![]() ,
вращается вокруг оси
,
вращается вокруг оси
![]() .
Тогда объем полученного тела вращения
вычисляется по формуле
.
Тогда объем полученного тела вращения
вычисляется по формуле
![]() .
.
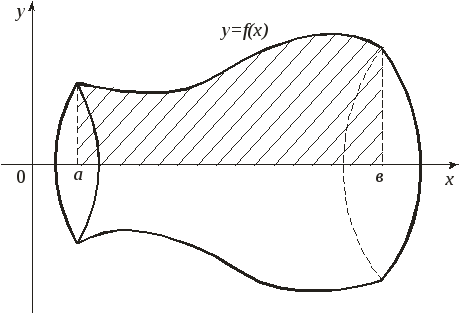
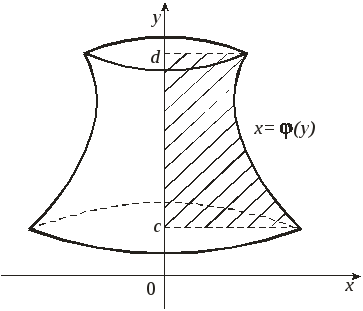
Объем тела,
полученного вращением вокруг оси Оу
криволинейной трапеции, ограниченной
прямыми у =
с и у
= d,
осью Оу
и графиком непрерывной на отрезке
![]() функции
функции
![]() ,
определяется по формуле
,
определяется по формуле
![]() .
.
Длина дуги плоской кривой
Пусть кривая
![]() ,
заданная уравнением
,
заданная уравнением
![]() ,
где
,
где
![]() ,
лежит в плоскости
,
лежит в плоскости
![]() :
:
Если функция
![]() и ее производная
и ее производная
![]() непрерывны на отрезке
непрерывны на отрезке
![]() ,
то длина дуги кривой
,
то длина дуги кривой
![]() вычисляется по формуле
вычисляется по формуле
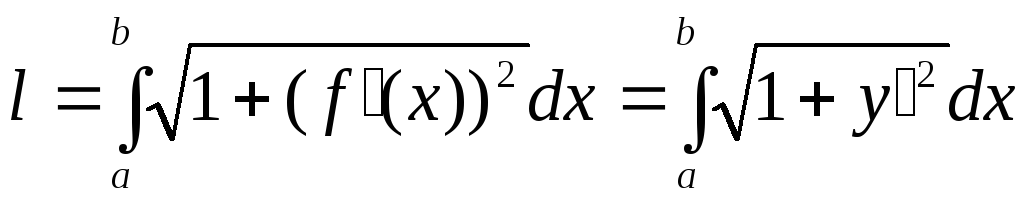 .
.
Несобственные интегралы с бесконечными пределами интегрирования
При введении
понятия определённого интеграла
![]() предполагалось, что выполняются следующие
два условия:
предполагалось, что выполняются следующие
два условия:
а) пределы
интегрирования а
и
![]() являются конечными;
являются конечными;
б) подынтегральная
функция
![]() ограничена на отрезке
ограничена на отрезке
![]() .
.
Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.
Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.
Определение 1.
Пусть функция
![]() определена и непрерывна на промежутке
определена и непрерывна на промежутке
![]() ,
тогда
,
тогда
![]()
называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).
Если
![]() существует и конечен, то несобственный
интеграл
существует и конечен, то несобственный
интеграл
![]() называется сходящимся;
если данный предел не существует или
равен
называется сходящимся;
если данный предел не существует или
равен
![]() ,
то несобственный интеграл называется
расходящимся.
,
то несобственный интеграл называется
расходящимся.
Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:
![]() .
.
Этот интеграл сходится, если предел в правой части равенства существует и конечен; в противном случае интеграл называется расходящимся.
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:
![]() ,
,
где
с
– любая точка интервала
![]() .
Интеграл
.
Интеграл
![]() сходится только в том случае, когда
сходятся оба интеграла в правой части
равенства.
сходится только в том случае, когда
сходятся оба интеграла в правой части
равенства.
Пример 2. Исследовать на сходимость несобственные интегралы:
а)
![]() ;
б)
;
б)
![]() .
.
Решение:
а)
![]()
![]() ,
следовательно,
данный интеграл расходится;
,
следовательно,
данный интеграл расходится;
б)
![]()
![]() Значит, несобственный
интеграл
Значит, несобственный
интеграл
![]() сходится и его значение равно
сходится и его значение равно
![]() .
.
