Задачи для самостоятельного решения
11. Дифференциальные уравнения
Решить дифференциальные уравнения с разделяющимися переменными:
1.
. 5.
.
2.
. 6.
.
3.
. 7.
.
4.
. 8.
.
Решить задачу Коши:
9.
.
10.
.
Решить однородные дифференциальные уравнения первого порядка:
11.
. 14.
.
12.
. 15.
.
13.
. 16.
.
Найти общие решения линейных дифференциальных уравнений первого порядка:
17.
. 20.
.
18.
. 21.
.
19.
. 22.
.
Решить задачу Коши:
23.
.
24.
.
12. Числовые ряды
Пусть задана бесконечная числовая последовательность
,
,
…,
,
…
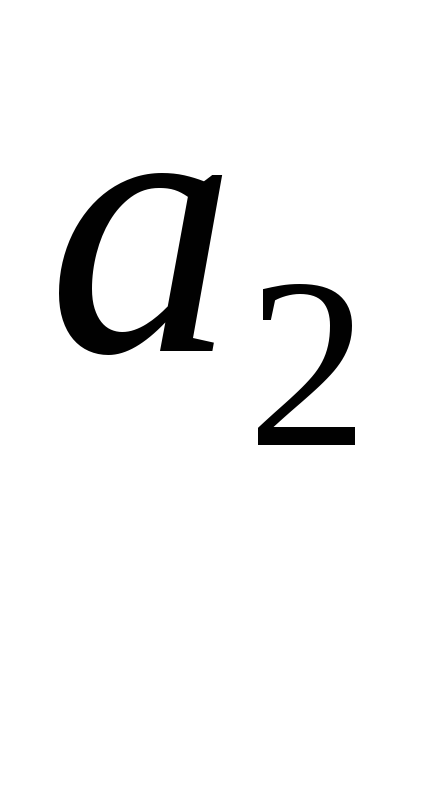Определение 1. Числовым рядом или просто рядом называется выражение (сумма) вида
. (1)
Числа
называются членами
ряда,
–
общим
или n–м
членом ряда.
Пример
1.
Пусть
.
Ряд
называется гармоническим рядом.
Пример
2.
Пусть
,
Ряд
называется
обобщенным гармоническим рядом.
В
частном случае при
получается гармонический ряд.
Пример
3.
Пусть
=
.
Ряд
называется рядом геометрической прогрессии.
Из
членов ряда (1) образуем числовую
последовательность
частичных
сумм
где
– сумма
первых членов ряда, которая называется
n-й
частичной суммой,
т. е.
,
,
,
…………………………….
, (2)
…………………………….
Числовая
последовательность
при неограниченном возрастании номера
может:
1) иметь конечный предел;
2) не иметь конечного предела (предел не существует или равен бесконечности).
Определение
2.
Ряд
(1) называется сходящимся,
если последовательность его частичных
сумм (2) имеет конечный предел, т. е.
В этом случае число
называется суммой
ряда (1) и пишется
.
Определение 3. Ряд (1) называется расходящимся, если последовательность его частичных сумм не имеет конечного предела.
Расходящемуся ряду не приписывают никакой суммы.
Теорема
1.
(Необходимый
признак сходимости ряда). Если
ряд (1) сходится, то его общий член
стремится к нулю при неограниченном
возрастании n,
т. е.
(3)
Следствие. (Достаточный признак расходимости ряда).
Если общий член
ряда
не стремится к нулю при
,
то этот ряд расходится.
Пример 4. Исследовать на сходимость ряд
.
Для этого ряда
Следовательно, данный ряд расходится.
Пример 5. Вычислить сумму ряда
.
Общий член ряда
представим
в виде
Тогда исходный
ряд можно представить в виде почленной
разности двух сходящихся рядов
геометрической прогрессии
Используя формулу
суммы бесконечно убывающей геометрической
прогрессии
,
вычислим суммы соответствующих рядов
геометрической прогрессии.
Для первого ряда
поэтому
.
Для второго ряда
поэтому
Окончательно имеем
.
Ряды с положительными членами. Признаки сходимости
Теорема 2. (Признак сравнения). Пусть даны два положительных ряда
, (4)
(5)
и выполняются
условия
,
начиная с некоторого номера n.
Тогда:
1) из сходимости ряда (5) следует сходимость ряда (4);
2) из расходимости ряда (4) следует расходимость ряда (5).
Теорема 3. (Признак Даламбера). Пусть члены положительного ряда (1) таковы, что существует предел
Тогда: 1) при q < 1 ряд (1) сходится;
2) при q > 1 ряд (1) расходится;
3) при q = 1 о сходимости ряда (1) ничего сказать нельзя, необходимы дополнительные исследования.
Замечание: ряд (1) будет расходиться и в том случае, когда
Пример 6. Исследовать на сходимость ряд
Применим признак Даламбера:
Следовательно, исходный ряд расходится.
Теорема 4. (Признак Коши). Пусть члены положительного ряда (1) таковы, что существует предел
Тогда: 1) при q < 1 ряд (1) сходится;
2) при q > 1 ряд (1) расходится;
3) при q = 1 о сходимости ряда (1) ничего сказать нельзя, необходимы дополнительные исследования.
Пример 7. Исследовать на сходимость ряд
Применим признак Коши:
Следовательно, исходный ряд сходится.
Теорема
5.
(Интегральный
признак Коши). Пусть
функция f(x)
непрерывная неотрицательная невозрастающая
функция на промежутке
Тогда
ряд
и
несобственный интеграл
сходятся или расходятся одновременно.