5.3. Задачі математичного програмування при нечітких обмеженнях

Нехай Х – універсальна множина альтернатив, – функція , значеннями якої оцінюються результати обирання альтернатив з множини Х. На множині Х подана нечітка підмножина , яку ми назвемо множиною допустимих альтернатив. Задача полягає у “максимізації” в деякому сенсі функції  на нечіткій множині .

Це означає, що під “максимізацією” можна розуміти вибір нечіткої підмножини множини (нечіткого рішення), якому відповідає в деякому сенсі найкраще нечітке значення функції . Ясно, що зображення рішення у такій формі має сенс лише тоді, коли ця форма змістовно зрозуміла ОПР.

Якщо ж ОПР не приймає нечіткого опису задачі, то під “максимізацію” функції  слід розуміти раціональний вибір конкретної альтернативи або множини альтернатив.

Раціональність при цьому означає, що при обиранні конкретної альтернативи ОПР повинна виходити з необхідності компромісу між бажанням отримати якомога більше значення функції  та бажанням обрати припустиму альтернативу, з можливо більшим значенням функції належності множини допустимих альтернатив.

Згідно з [ ], розглянемо два підходи до розв’язування цієї задачі.

5.3.1. Розв’язок 1, який базується на множинах рівня нечіткої множини обмежень

Цей підхід полягає у тому, що вихідна задача нечіткого математичного програмування формулюється у вигляді сукупності звичайних задач максимізації функції  на всіляких множинах рівня множини допустимих альтернатив. Якщо ж альтернатива є розв’язком задачі на множині рівня , то грубо кажучи, можна вважати, що число  є степенем належності альтернативи до нечіткої множини розв’язків задачі НМП.

Таким чином, перебравши всілякі значення , ми одержуємо функцію належності нечіткого розв’язку.

Опишемо цей підхід більш детально.

Позначимо через множину рівня  нечіткої множини допустимих альтернатив . Тобто

.

Для такого, що. Введемо множину

.

Множина є множиною розв’язків звичайної задачі максимізації функції  на множині тих альтернатив, які зі степенем не меншим  вважаються допустимими у вихідній задачі НМП.

Для побудови функції належності нечіткого розв’язку необхідно кожній альтернативі приписати степінь належності до цієї множини. Зробимо це таким чином. Степенем належності альтернативи нечіткій множині розв’язків будемо вважати максимальне (точніше верхню границю) з чисел , для яких існує .

О з н а ч е н н я  5.2. Розв’язком задачі НМП будемо називати нечітку підмножину , яка описується функцією належності виду

. (5.1)

Або, в простішій формі, має місце таке твердження:

Т в е р д ж е н н я  5.1. Якщо , то .

Доведення

а) Якщо й , то. Це означає, що існує таке , що і , згідно означення нечіткого рішення і тому , тобто нерівність неможлива.

б) Якщо й або

, (5.2)

то для будь-якого  такого, що , виконується , крім того, , тому що в протилежному випадку з (5.2) маємо Звідсіль випливає, що

.

Тим самим твердження доведено.

Із твердження 5.1. і визначення розв’язку випливає, що розв’язок задачі НМП може бути поданий у вигляді

(5.3)

і таким чином:

.

Будемо говорити, що розв’язок 1 існує, якщо на множині Х, тобто розв’язок 1 існує тоді й тільки тоді, коли знайдеться таке число  > 0, що .

Нечіткому розв’язку відповідає нечітке “максимальне” значення функції . Воно є образом нечіткої множини при відображенні .

Згідно визначенню образа отримуємо:

, (5.4)

де

.

Якщо у задачі НМП розв’язку 1 не існує, то можемо скористатися ‑оптимальним нечітким розв’язком, яке для поданого  > 0 можна визначити таким чином:

, (5.5)

де . (5.6)

Відповідне нечітке значення функції  описується функцією належності

. (5.7)

Границю при можна вважати верхньою нечіткою границею функції  на нечіткій множині . Поняття -оптимального розв’язку корисно не тільки тоді, коли при будь-якому , але й тоді, коли при деяких  із [0,1].

Розглянемо властивості розв’язку 1.

1. Для будь-якого такого, що , знайдеться така альтернатива , що й при деякому  > 0. Тобто

. (5.8)

2. Якщо , то

3. Функція монотонно спадає на множині .

Функція визначена таким чином, що її значення для даного є максимальним степенем належності альтернативи х множині , на якій функція приймає значення r.

Відповідно властивості 3 функція монотонно спадає на множині . Це означає, зокрема, що у множині Х немає жодної альтернативи, для якої виконувалися б одночасно нерівності й , тобто немає такого елемента , який мав би більшу ніж степінь належності й дав би більше за r значення функції, що максимізується.

Якщо ОПР бажає обрати за розв’язок конкретну альтернативу , то її обирання повинно спиратися не тільки на степінь належності цієї альтернативи до нечіткої множини , але й на відповідне значення функції . Як випливає з властивості 3 чим більше значення , тим менше значення степеня належності тієї альтернативи, яка дає значення . Тому ОПР повинна спочатку звернутися до нечіткого максимального значення функції та обрати пару , яка відповідає його бажанню отримати більше значення й в той же час можливо більше значення степеня належності обраного до множини . Після обирання такої пари доречно обрати таку альтернативу , яка має найбільший степінь належності множині (або альтернативу, яка в деякому сенсі близька до х).

Описаний підхід є незручним з двох причин.

По-перше, у одержаному розв’язку недостатньо явно враховується необхідність компромісу між значеннями функції, що максимізується й значеннями степеня належності допустимої альтернативи.

По-друге, цей розв’язок незручний для обчислювань.

Якщо функція належності неперервна, то застосування цього підходу необхідно розглядати нескінченну кількість задач, оскільки нескінченною буде кількість множин рівня. однак для практичного використання достатньо розглянути скінченну множину задач для множин рівня, що визначені експертами або ОПР.

Розглянемо застосування цього підходу для лінійної задачі НМП.

П р и к л а д  5.3. Розв’язати задачу нечіткого математичного програмування:

Якщо нечіткі обмеження описуються функцією належності виду

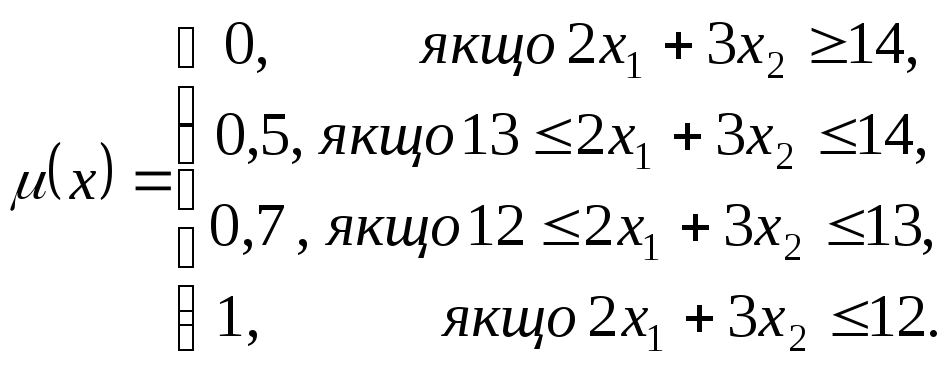
Розв’язування

Для розв’язування задачі будемо використовувати метод розкладання на множини рівня. Тобто послідовно будемо розв’язувати задачі на множинах рівня ₁ = 1; ₂ =0,7; та ₃ = 0,5.

Для рівня ₁ = 1 , наприклад, задача набуває виду:

Для рівня ₂ =0,7:

Для рівня ₃ = 0,5:

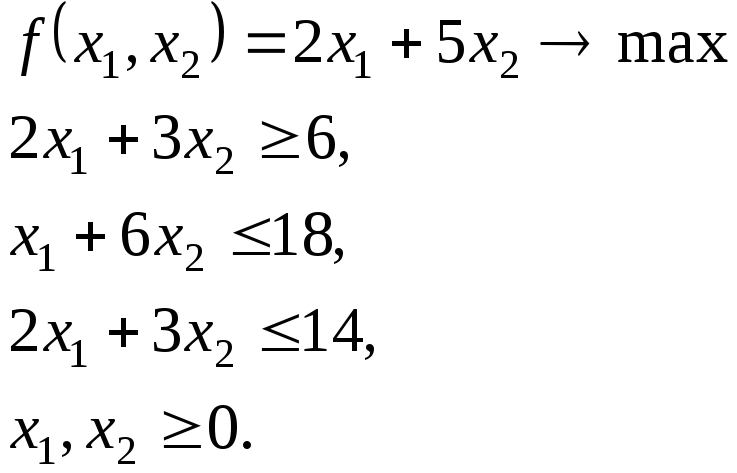
Це задачі лінійного програмування і для їх розв’язування можна застосовувати, наприклад симплекс-метод, або, оскільки в нашому випадку тільки дві змінні використати графічне рішення.

Розв’яжемо задачу графічно. Зобразимо на координатній площині множини рівня для нечіткої множини припустимих альтернатив (див. рис. 5.2).

Рис. 5.2. Графічне розв’язування задачі нечіткого математичного

програмування

Тут ABCDE – множина рівня ₁ = 1; A₁ DCDE₁ – множина рівня ₂ =0,7; A₂ BCDE₂ – множина рівня ₃ = 0,5.

Розв’язком задачі на множині рівня 1 буде точка А. Знайдемо її координати з системи рівнянь:

отримуємо

Значення функції у цій точці .

Аналогічно находимо розв’язки на множинах рівня 0,7 та 0,5. Це точки А₁ з координатами та А₂ (її координати ). Відповідні значення функції цілі , .

Поєднуючи результати одержуємо нечіткий розв’язок задачі:

х1	х2	f	
2			1
			0,7
			0,5

Зауважимо, що якщо функції належності неперервні, то необхідно розв’язувати задачі на нескінченній кількості множин рівня. Але на практиці достатньо визначити декілька рівнів, які повинні бути розглянуті.