
- •Математическая статистика Введение в математическую статистику
- •Предмет математической статистики
- •Возникновение и развитие математической статистики
- •Приложения математической статистики
- •Общая статистическая модель
- •Параметрические и непараметрические задачи
- •Случайные величины и статистики
- •Достаточные статистики
- •Критерий факторизации.
- •Выборка и эмпирическая мера
- •Выбор статистической модели
- •Классическая статистическая модель.
- •Эмпирическая функция распределения
- •Выборочные характеристики
- •Свойства выборочных характеристик
- •Моделирование выборок на компьютере
- •Датчик случайных чисел
- •Моделирование дискретных распределений
- •Моделирование непрерывных распределений
- •Метод максимального правдоподобия
- •Байесовский подход
- •Допустимость байесовских оценок
- •Теорема об апостериорном риске
- •Вычисление байесовских оценок при квадратичной функции потерь
- •Минимаксный подход
- •Минимаксность байесовских решений
- •Проверка статистических гипотез
- •Основные понятия теории проверки статистических гипотез
- •Проверка двух простых гипотез
- •Байесовский подход
- •Наиболее мощный критерий. Лемма Неймана- Пирсона
- •Проверка непараметрических гипотез. Критерии согласия
- •Критерий знаков
- •Состоятельность критерия
- •Критерий Колмогорова
- •Критерий хи-квадрат
- •Асимптотические доверительные интервалы
- •Доверительные интервалы для параметров нормального распределения
Выборочные характеристики
Следующие функции от выборки называются выборочными характеристиками. Это
-
Выборочное среднее
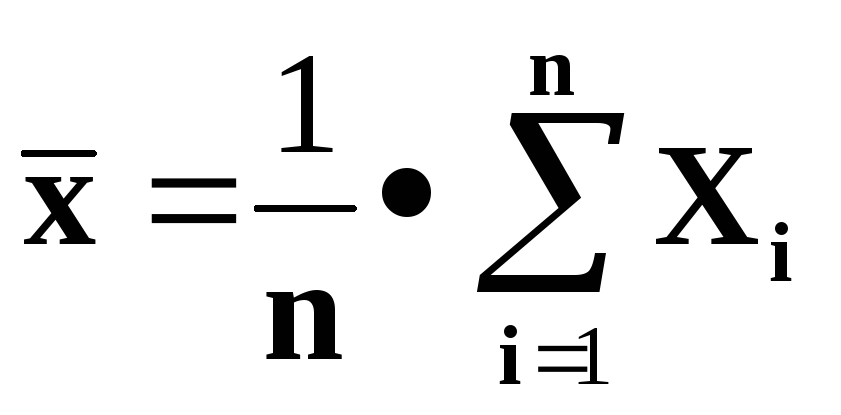
-
Выборочная дисперсия
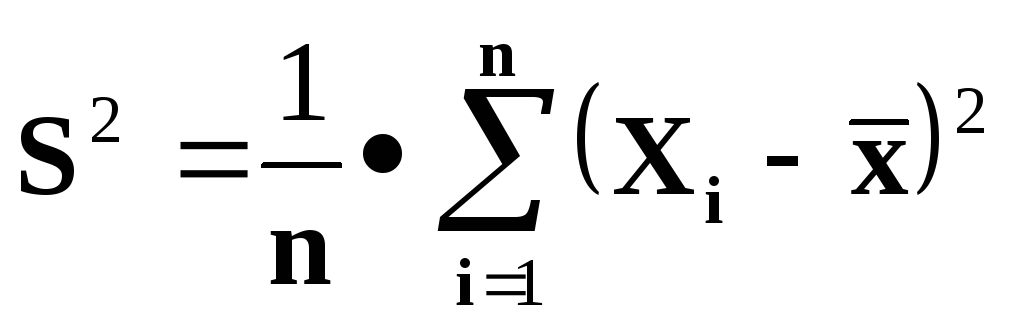
-
Несмещенная выборочная дисперсия
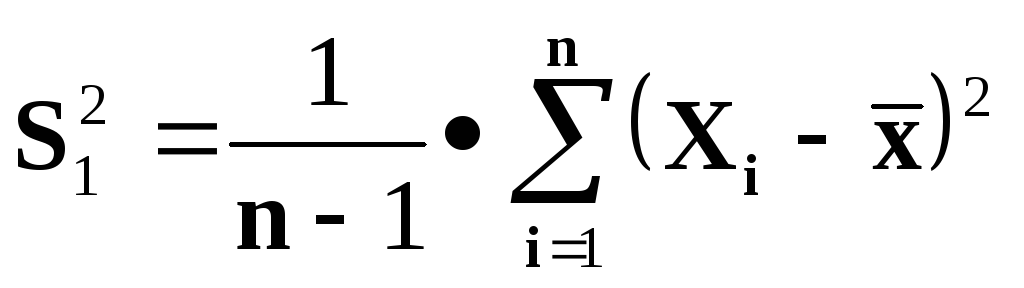
-
Минимальная порядковая статистика
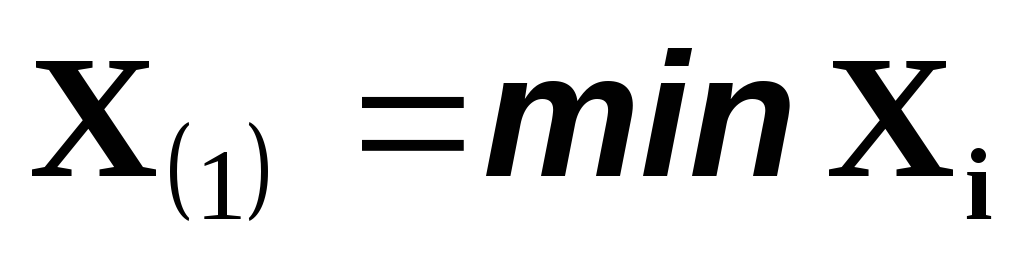
-
Максимальная порядковая статистика
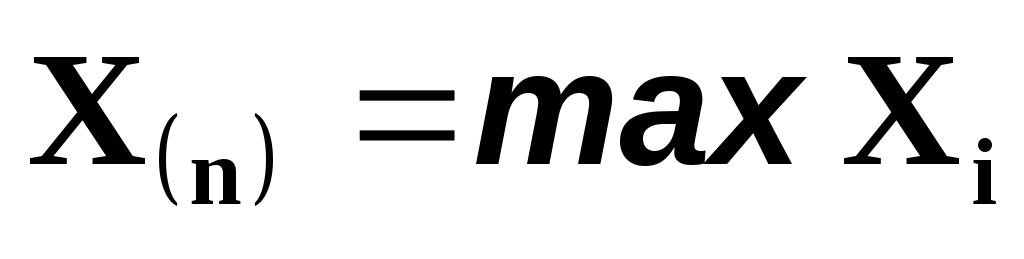
-
 -тая
порядковая статистика
-тая
порядковая статистика
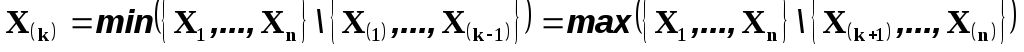
-
Медиана
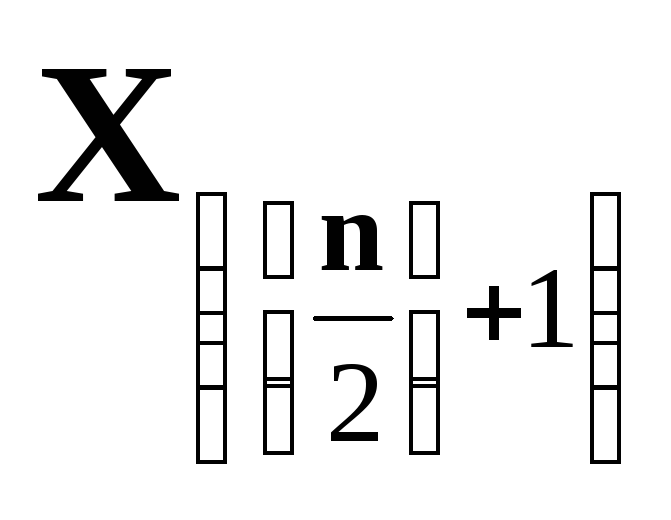
-
Вариационный ряд выборки
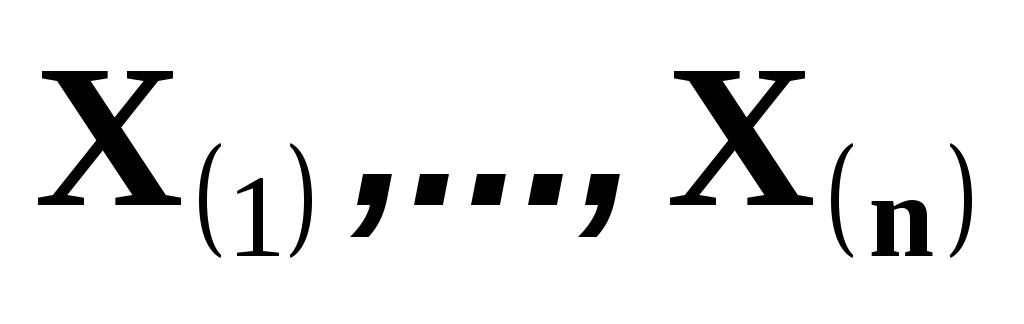
Эти характеристики позволяют компактно представить часть информации, содержащейся в выборке, и часто естественным образом возникают при решении статистических задач.
Свойства выборочных характеристик
Пользуясь методами
теории вероятностей (свойства
математического ожидания и дисперсии,
закон больших чисел и центральная
предельная теорема), нетрудно получить
(в априорном предположении о существовании
достаточного числа моментов у случайной
величины
![]() )
следующие свойства выборочных
характеристик.
)
следующие свойства выборочных
характеристик.
-
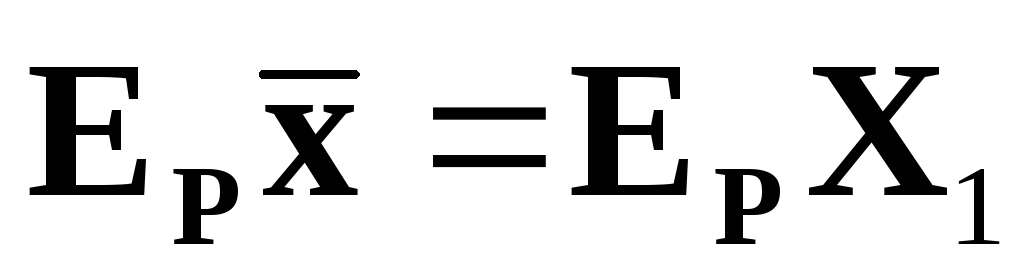
-
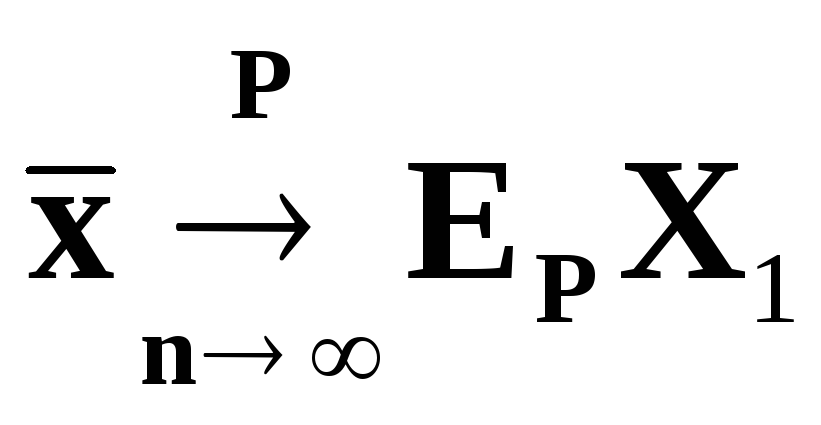
-
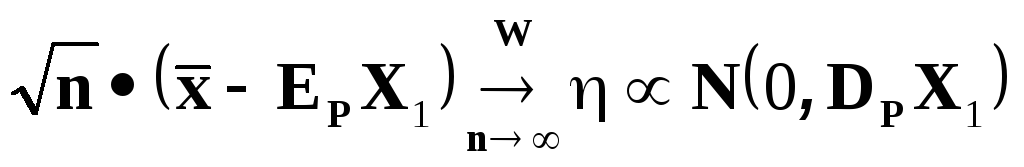
-
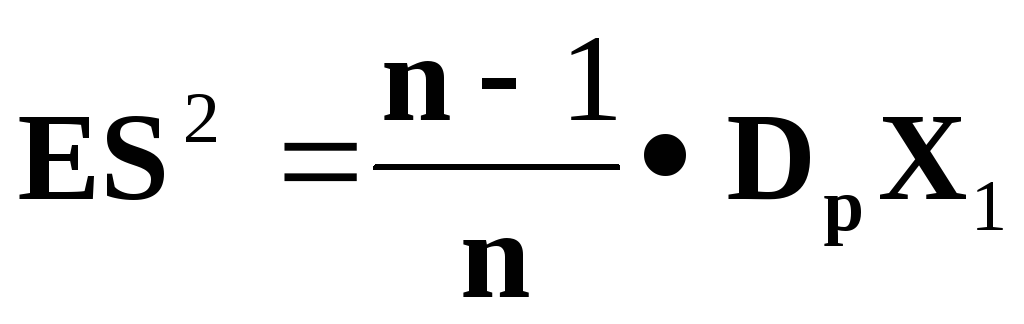
-
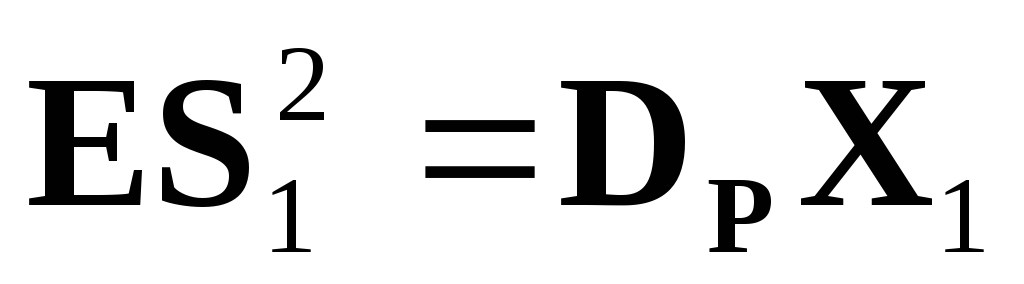
-
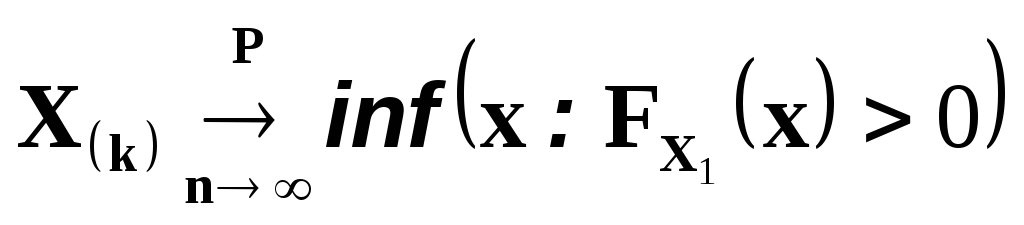
-
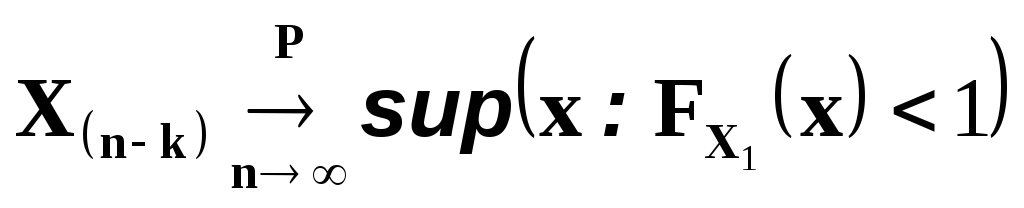
-
Если функция распределения данных
 непрерывна, то при
непрерывна, то при
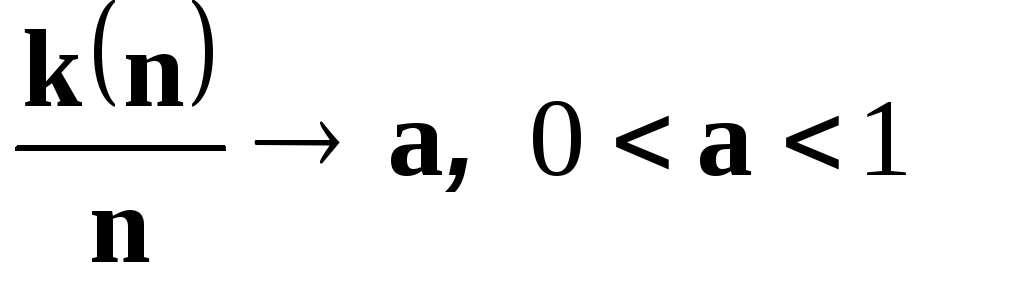
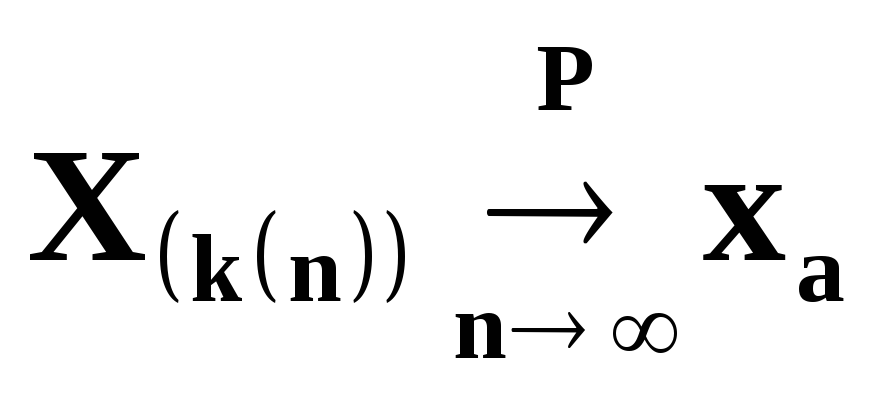 где
где
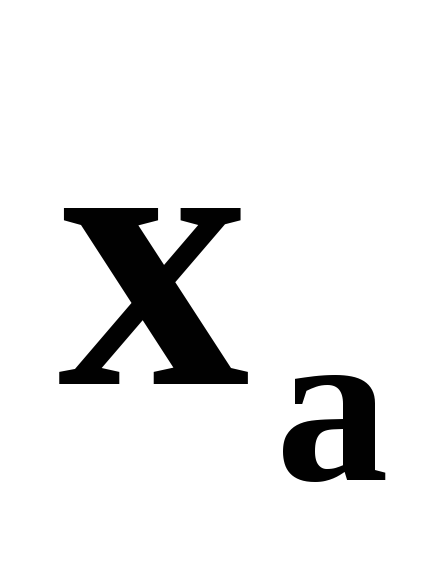 - так называемая
- так называемая
 -
квантиль, т. е. корень уравнения
-
квантиль, т. е. корень уравнения

Моделирование выборок на компьютере
Моделирование числовых выборок на компьютере позволяет проиллюстрировать основные теоремы и методы классической статистики и рассчитать те характеристики статистических процедур, теоретический расчет которых затруднителен или невозможен.
Основная задача
моделирования в этом случае – моделирование
последовательности независимых значений
некоторой числовой случайной величины
(моделирование конкретного распределения).
Обычно эту задачу разбивают на два
этапа. Сначала моделируют последовательность
значений базовой случайной величины,
обычно равномерно распределенной на
отрезке
![]() ,
затем преобразуют эту последовательность.
,
затем преобразуют эту последовательность.
Датчик случайных чисел
Датчиком случайных
чисел обычно называют программу,
подпрограмму или функцию, которая
обеспечивает построение последовательности
чисел, моделирующих выборку из
равномерного распределения на отрезке![]() .
В языках программирования эти функции
обычно называются так: rand(),
random() и т.п. Теория построения
таких функций изложена, например, в
книге Кнута «Искусство программирования
для ЭВМ», том 2.
.
В языках программирования эти функции
обычно называются так: rand(),
random() и т.п. Теория построения
таких функций изложена, например, в
книге Кнута «Искусство программирования
для ЭВМ», том 2.
Последовательность
независимых равномерно распределенных
чисел на отрезке
![]() будем
обозначать
будем
обозначать
![]()
Моделирование дискретных распределений
Моделирование конкретного распределения можно производить различными способами. Если распределение дискретно, то можно использовать, например, следующий прием.
Пусть
![]() - разбиение отрезка
- разбиение отрезка![]() ,
тогда последовательность
,
тогда последовательность
![]()
является
последовательностью независимых
дискретных случайных величин, принимающих
значения
![]() с вероятностями
с вероятностями
![]() .
.
Например, для
моделирования распределения
![]() достаточно разбить отрезок
достаточно разбить отрезок
![]() на две части длиной
на две части длиной
![]() и
и
![]() ,
соответственно. Для моделирования
распределения
,
соответственно. Для моделирования
распределения![]() применять предложенный метод нерационально,
так как придется вычислять вероятности
вида
применять предложенный метод нерационально,
так как придется вычислять вероятности
вида
![]() .
.
Гораздо проще для
моделирования![]() сложить
сложить![]() смоделированных величин
смоделированных величин
![]() .
Заметим, что для моделирования одной
величины
.
Заметим, что для моделирования одной
величины
![]() в этом случае потребуется
в этом случае потребуется
![]() членов последовательности
членов последовательности![]()
Моделирование непрерывных распределений
Моделирование конкретного распределения можно производить различными способами. Если распределение непрерывно, то можно использовать, например, следующий прием.
Пусть
![]() -
непрерывная функция распределения,
тогда последовательность
-
непрерывная функция распределения,
тогда последовательность
![]()
является
последовательностью независимых
случайных величин, принимающих значения
с функцией распределения![]() .
.
Для доказательства
достаточно вычислить функцию распределения
случайной величины
![]() .
.
Например, для
моделирования распределения
![]() достаточно положить
достаточно положить
![]()
Для моделирования
распределения![]() применять предложенный метод нерационально,
так как придется вычислять обратную
функцию к функции вида
применять предложенный метод нерационально,
так как придется вычислять обратную
функцию к функции вида![]() .
.
Гораздо проще для
моделирования![]() сложить
сложить![]() смоделированных величин
смоделированных величин
![]() .
Заметим, что для моделирования одной
величины
.
Заметим, что для моделирования одной
величины
![]() в этом случае потребуется
в этом случае потребуется
![]() членов последовательности
членов последовательности![]()
Моделирование нормального распределения.
Для моделирования стандартного нормального распределения можно использовать следующее утверждение.
Утверждение.
Случайные величины
![]()
![]()
независимы и стандартно нормально распределены.
Доказательство этого утверждения представляет собой упражнение из математического анализа на замену переменных в двумерном интеграле (переход к полярным координатам).
Теория оценивания
В данном и следующих разделах по умолчанию предполагается существование необходимого числа моментов у случайных величин.
Если в утверждениях
появляется параметр
![]() ,
то это означает, что рассматривается
выборка размера
,
то это означает, что рассматривается
выборка размера
![]() .
.
Определение оценки и критерии качества оценок
Определение.
Статистика
![]() называется оценкой параметра
называется оценкой параметра
![]() ,
если она принимает свои значения в
параметрическом множестве
,
если она принимает свои значения в
параметрическом множестве
![]() .
.
Разумными требованиями к оценкам являются
-
Несмещенность
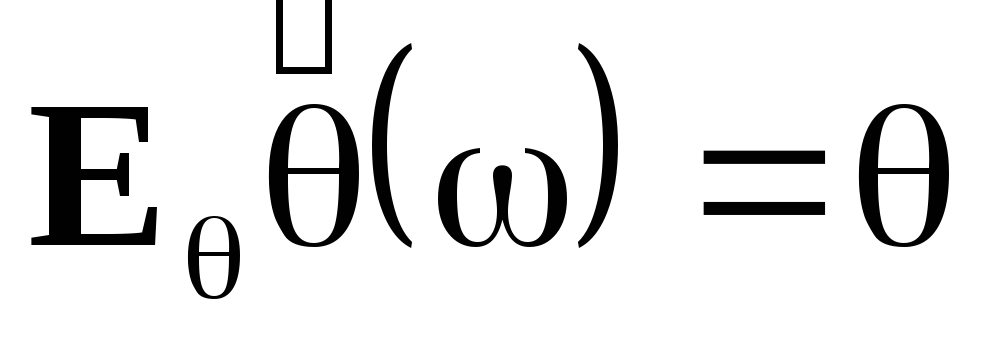
-
Состоятельность
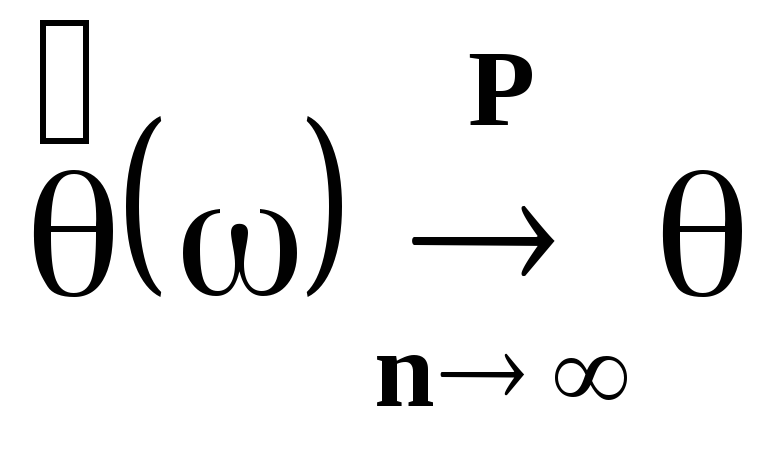
-
Минимальность дисперсии
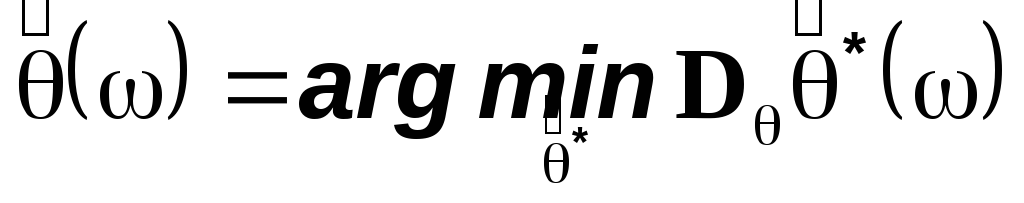
Общие методы построения оценок
Идеальная или оптимальная оценка должна удовлетворять всем требованиям 1)-3). Однако нет гарантии, что такая оценка существует. Поэтому интересными являются также методы, позволяющие строить оценки, удовлетворяющие, например, требованию 2) или требованиям 2) и 1)
Метод подстановки и метод моментов
Метод подстановки
заключается в использовании идеи
подстановки и применяется в случае,
когда данные представляют собой выборку.
Пусть существуют такие измеримые
функции
![]() и
и
![]() ,
что
,
что
![]()
тогда оценкой по методу постановки называется величина
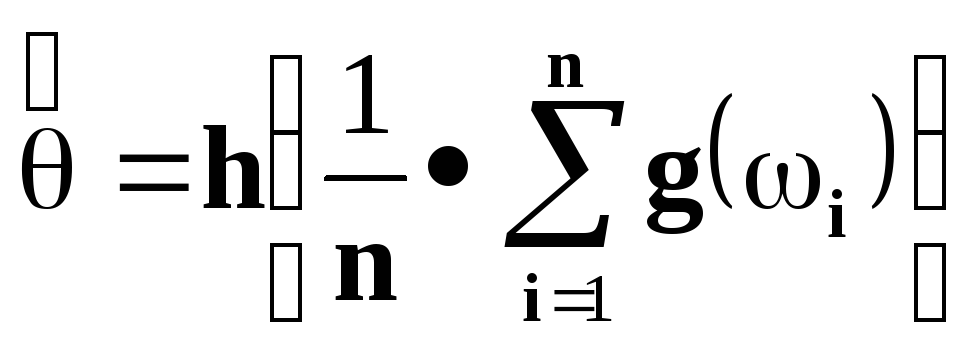
Теорема.
Если функция
![]() линейна, то оценка по методу подстановки
несмещена и состоятельна, если непрерывна,
то состоятельна.
линейна, то оценка по методу подстановки
несмещена и состоятельна, если непрерывна,
то состоятельна.
Метод моментов.
Суть метода моментов заключается в следующем. Очевидно, выборочные среднее и дисперсия являются несмещенными оценками своих математических ожиданий, являющихся в параметрическом случае некоторыми функциями от параметра.
![]()
![]()
Если функции![]() и
и
![]() непрерывны и монотонны, то существуют
обратные к ним функции и, применяя метод
подстановки, получим оценки
непрерывны и монотонны, то существуют
обратные к ним функции и, применяя метод
подстановки, получим оценки
![]()
![]()
Очевидно, что подобным образом можно использовать другие выборочные характеристики.
