Байесовский подход

В байесовском подходе к решению задачи оценивания предполагается, что параметр является случайной величиной с некоторым распределением. Формально, на задается некоторая мера и предполагается , что случайная величина имеет плотность относительно меры .

Эту плотность называют априорной плотностью .

Определение.

Байесовским риском решающего правила называется величина

Определение.

Байесовским решающим правилом называется решающее правило

Заметим, что количество различных байесовских оценок при одном и том же распределении данных велико (в принципе, каждому априорному распределению может соответствовать своя байесовская оценка ).

Допустимость байесовских оценок

Множество байесовских оценок близко к множеству допустимых оценок.

Теорема об апостериорном риске

Следующая теорема позволяет указать путь для вычисления байесовских оценок

Теорема (об апостериорном риске)

Случайная величина

называется апоcтериорным риском (a posteriori = после опыта) решающего правила .

Условная плотность

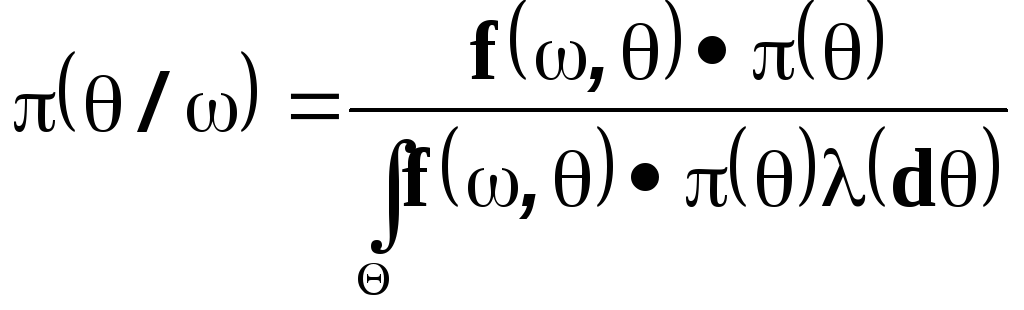
называется апостериорной плотностью .

Вычисление байесовских оценок при квадратичной функции потерь

Если параметр одномерен и функция потерь квадратична, т.е.

то для байесовского решения можно выписать простое представление

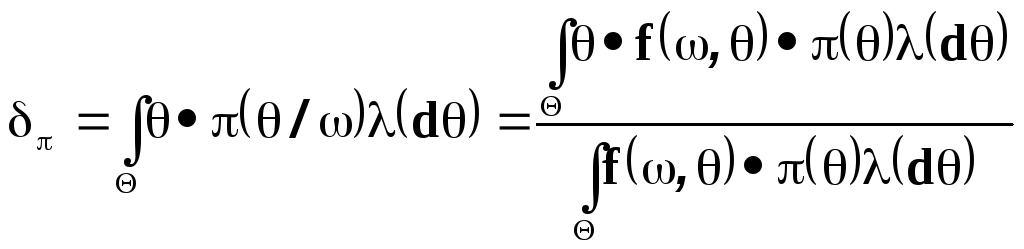
Доказательство следует из того, что по выражение

представляет собой квадратный трехчлен.

Пример

Пусть вектор данных представляет собой выборку из распределения и априорное распределение параметра также нормальное . Тогда апостериорная плотность нормальна и

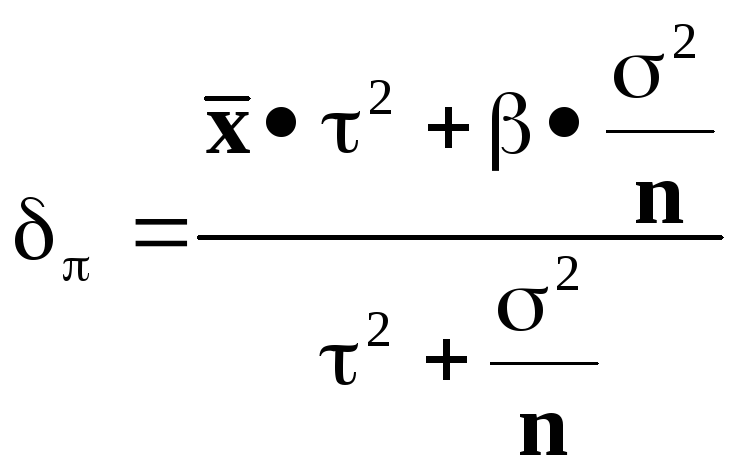
Минимаксный подход

В минимаксном подходе предлагается застраховаться от больших потерь. Именно

Определение

Решающее правило называется минимаксным решающим правилом если

Поиск минимаксного решающего правила обычно более труден, чем поиск байесовского в той же задаче. Однако в ряде случаев байесовская оценка является также и минимаксной.

Минимаксность байесовских решений

Теорема (минимаксность байесовских оценок)

Пусть - байесовская оценка и

Тогда

Пример.

Пусть вектор данных представляет собой выборку из распределения . Тогда, если выбрать априорное распределение параметра бета распределением , то апостериорная плотность также будет бета плотностью и решение задачи на определение параметров таких, что

приводит к значениям

и минимаксная оценка имеет вид

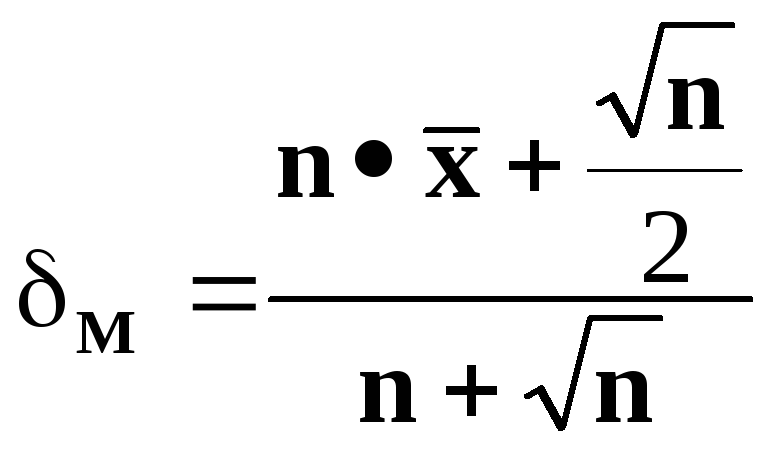
Проверка статистических гипотез

В ряде случаев необходимо выбрать, какому из двух или нескольких предположений относительно семейства лучше соответствуют данные.

Основные понятия теории проверки статистических гипотез

Пусть относительно семейства есть два предположения (две гипотезы)

и

В математической статистике принято называть эти предположения гипотезами и обозначать так

Гипотезу обычно называют основной гипотезой, а гипотезу - альтернативной гипотезой (или, короче, альтернативой).

Критерием проверки гипотезы называют отображение

указывающее номер (истинной) гипотезы в зависимости от данных.

С точки зрения теории статистических решений, на первый взгляд, задача проверки статистических гипотез это задача с двумя возможными решениями и критерий есть просто решающее правило в такой задаче. Обозначим его . Однако, так как каждое из семейств и 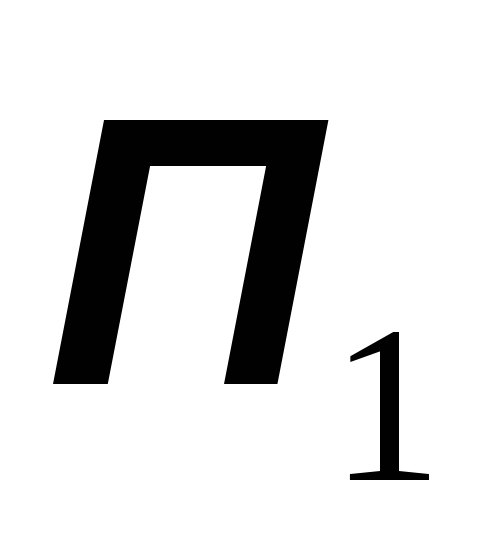может содержать больше одного распределения, то при определении потерь должно учитываться, какое из распределений реализовалось в опыте (истинно) и какое семейство выбрано с помощью критерия.

Множество называется критическим множеством или критической областью.

Гипотезы, семейства которых содержат только одно распределение, называются простыми, в противном случае – сложными.