13. Спектр неперіодичного сигналу на нескінченному інтервалі зміни аргументу.

14. Перетворення Фур’є. Визначення. Загальні відомості.

Преобразование Фурье является инструментом спектрально­го анализа непериодических сигналов. Впрочем, чуть позже мы увидим, что его можно применять и к сигналам периодическим, но это потребует использования аппарата обобщенных функций.

Для наглядной иллюстрации перехода от ряда Фурье к преобразованию Фурье часто используется не вполне строгий математически, но зато понятный подход. Представим себе периодическую последовательность импульсов произвольно­го вида и сформируем ряд Фурье для нее. Затем, не меняя формы одиночных импульсов, увеличим период их повторения (заполнив промежутки нулевым значением) и снова рассчитаем коэффициенты ряда Фурье. Формула (1.9) для расчета коэффициентов ряда показывает, что нам придется вычислить тот же самый интеграл, но для более тесно расположенных частот =к_{. Изменение пределов интегрирования не играет роли — ведь на добавившемся между им­пульсами пространстве сигнал имеет нулевое значение. Единственное дополни­тельное изменение будет состоять в уменьшении общего уровня гармоник из-за деления результата интегрирования на увеличившийся период Т.

На рис. 1.9 описанные изменения иллюстрируются на примере двукратного уве­личения периода следования прямоугольных импульсов. Обратите внимание на то, что горизонтальная ось спектральных графиков проградуирована в значени­ях частот, а не номеров гармоник.

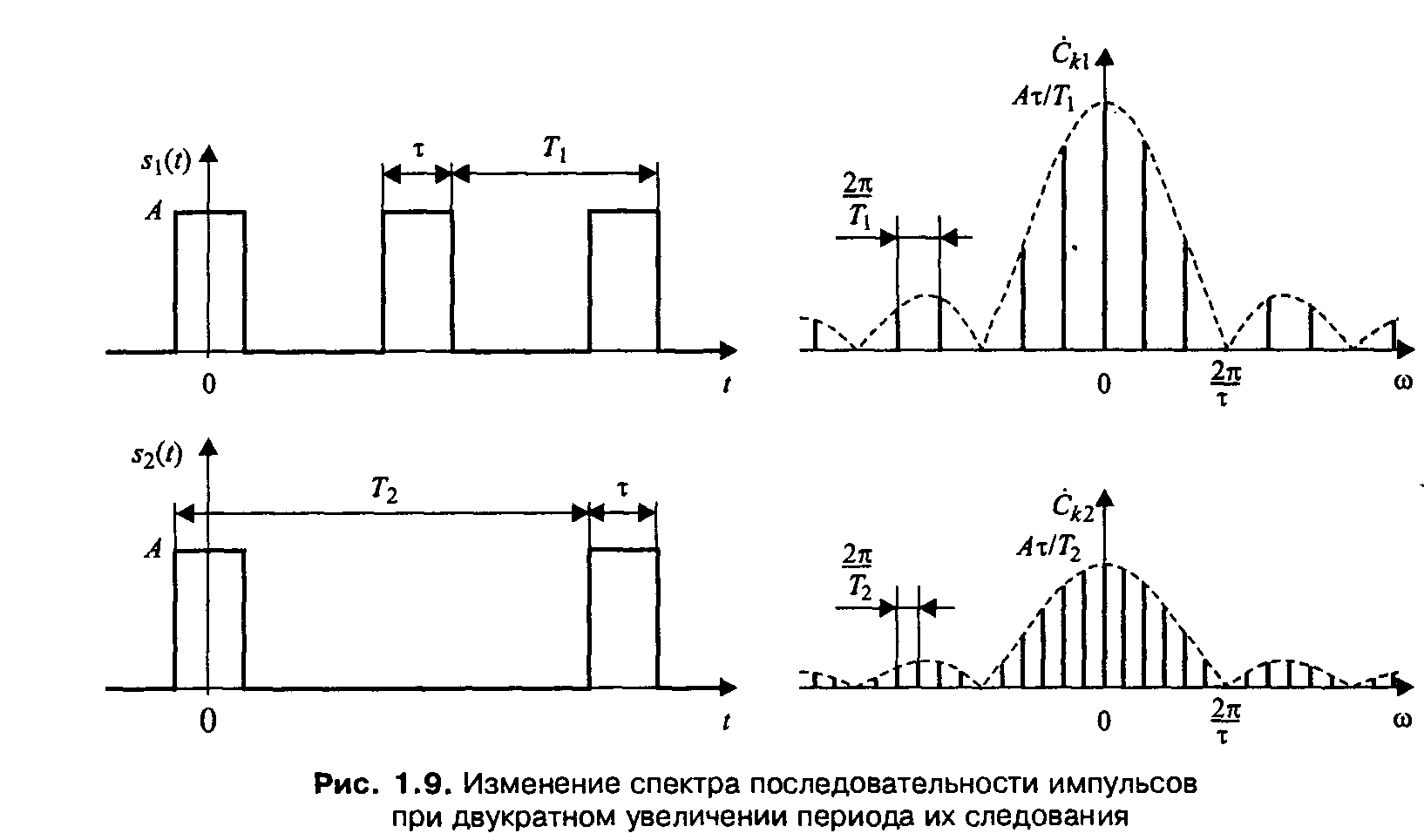
Итак, с ростом периода следования импульсов гармоники располагаются ближе друг к другу по частоте, а общий уровень спектральных составляющих становит­ся все меньше. При этом вид вычисляемого интеграла (1.9) не меняется.

Наконец, если устремить период к бесконечности (превратив тем самым перио­дическую последовательность в одиночный импульс), гармоники спектра будут плотно занимать всю частотную ось, а их амплитуды упадут до нуля (станут бес­конечно малыми). Однако взаимное соотношение между уровнями гармоник ос­тается неизменным и определяется все тем же интегралом (1.9). Поэтому при спектральном анализе непериодических сигналов формула для расчета коэффи­циентов комплексного ряда Фурье модифицируется следующим образом:

* частота перестает быть дискретно меняющейся и становится непрерывным параметром преобразования (то есть к1 в формуле (1.9) заменяется на со);

□ удаляется множитель 1/Т;

□ результатом вычислений вместо нумерованных коэффициентов ряда явля­ется функция частоты S() — спектральная функция сигнала Иногда ее называют также спектральной плотностью.

В результате перечисленных модификаций формула (1.9) превращается в фор­мулу прямого преобразования Фурье:

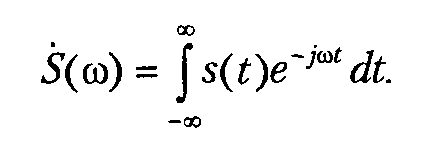
В формуле самого ряда Фурье суммирование, естественно, заменяется интегри­рованием (и, кроме того, перед интегралом появляется деление на 2pi). Получаю­щееся выражение называется обратным преобразованием Фурье:

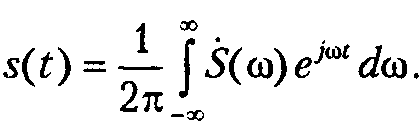
Чтобы преобразование Фурье было применимо, сигнал должен удовлетворять следующим требованиям:

□ должны выполняться условия Дирихле (см. раздел «Ряд Фурье»);

□ сигнал должен быть абсолютно интегрируемым. Это означает, что интеграл от его модуля должен быть конечной величиной:

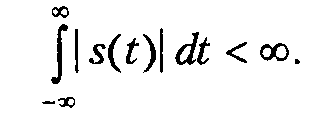
Однако с привлечением математического аппарата обобщенных функций воз­можно выполнение Фурье-анализа и для некоторых сигналов, не удовлетворяю­щих этим требованиям (речь об этом пойдет далее, в разделе «Фурье-анализ не-интегрируемых сигналов»).

Если анализируемый сигнал S(t) — вещественная функция, то соответствующая спектральная функция S() является «сопряженно-симметричной» относитель­но нулевой частоты. Это означает, что значения спектральной функции на часто­тах и -) являются комплексно-сопряженными по отношению друг к другу:

Если S(t) — четная функция, то, как и в случае ряда Фурье, спектр будет чисто вещественным (и, следовательно, будет являться четной функцией). Если, на­против, S(t) — функция нечетная, то спектральная функция S() будет чисто мнимой (и нечетной).

Модуль спектральной функции часто называют амплитудным спектром, а ее аргумент — фазовым спектром. Легко показать, что для вещественного сигнала амплитудный спектр является четной, а фазовый — нечетной функцией частоты:

Примеры расчета спектральных функций конкретных сигналов и соответствую­щие графики будут приведены далее.

Итак, преобразование Фурье (1.11) ставит в соответствие сигналу, заданному во времени, его спектральную функцию. При этом осуществляется переход из вре­менной области в частотную. Преобразование Фурье является взаимно-одно­значным, поэтому представление сигнала в частотной области (спектральная функция) содержит ровно столько же информации, сколько и исходный сигнал, заданный во временной области.