3.3. Методы классификации образов

Метод решающих функций. Уравнение разделяющей прямой

d(x) = w₁x₁+w₂x₂+w₃ = 0

обеспечивает значение d(x)>0 для любого образа объекта из класса W₁ и d(x)<0 для любого образа объекта из класса W₂.

Таким образом, знак функции d(x) при подстановке значений признаков каждого конкретного объекта позволяет классифицировать этот объект. Функцию d(x) можно использовать в качестве решающей (или дискриминантной) функции.

Как будет видно в дальнейшем, этот метод нетрудно распространить на большее число классов, на классы с большим числом признаков, а также на случай нелинейных границ в любом конечномерном евклидовом пространстве.

Успех применения данной схемы зависит от двух факторов:

1. вида самой функции;

2. возможности определения ее коэффициентов.

В n-мерном случае функция d(x) имеет вид:

d(x) = w₁x₁+w₂x₂+w₃x₃+…+ w_nx_n + w_n+1= wx + w_n+1,

где вектор w называют весовым или параметрическим.

Часто последнее уравнение пишут в форме

d(x) = w`x,

где w`= (w₁, w₂, w₃, …, w_n, w_n+1), а x = (x₁, x₂, x₃, …, x_n, 1) – пополненные векторы весов и образов  соответственно. Пример линейной решающей функции для случая двух признаков дан на рис. 3.1. Предполагается, что в случае разбиения на два класса решающая функция d(x) обладает свойством:

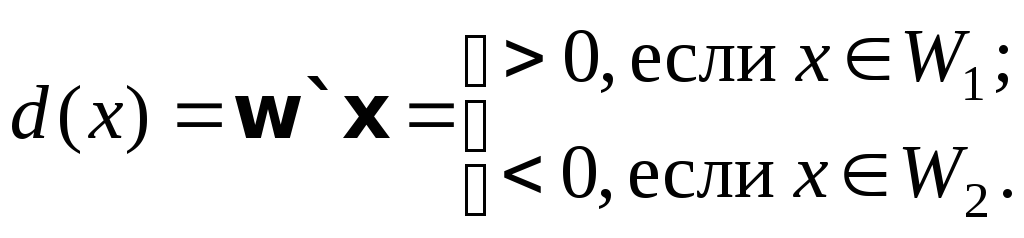
Рассмотрим случаи разбиения на несколько классов.

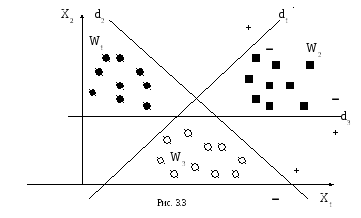
Случай 1. Каждый класс отделяется от остальных одной разделяющей поверхностью (рис. 3.3). В этом случае существует M разделяющих поверхностей и, соответственно, M решающих функций со свойствами:

где индекс i = 1, 2, 3, …, M, а весовой вектор w_i = (w_1i, w_2i, w_3i, …, w_{n i}, w_{n+1, i})  весовой вектор, соответствующий i-й решающей функции.

Пусть решающие функции имеют вид

d₁(x) = x₁+x₂, d₂(x) = x₁+x₂5, d₃(x) = x₂ +1.

Соответственно три разделяющие границы определяются уравнениями:

x₁+x₂ = 0, x₁+x₂=5, x₂ = 1.

Любой образ, для которого выполняются условия d₁(x)>0, d₂(x)<0 и d₃(x)<0, зачисляется в класс W₁, при d₁(x)<0, d₂(x)>0 и d₃(x)<0  в класс W₂, при d₁(x)<0, d₂(x)<0 и d₃(x)>0  в класс W₃. Например, образ x=(6,5) дает d₁(x)=1, d₂(x)= 6 и d₃(x)= 4. Это позволяет зачислить его в класс W₂.

Следует отметить, что в областях, где вектор x дает более одного положительного результата, или все отрицательные  данная схема разделения не срабатывает. Это – области неопределенных решений. Объект в этом случае относиться сразу к двум или же ни к одному классу.

Случай 2. Каждый класс отъединяется от любого другого отдельной разделяющей поверхностью. Классы попарно разделимы. В этом случае существует M(M-1)/2 (число сочетаний из M по 2) поверхностей (рис. 3.4). Разделяющие функции имеют вид

d_ij(x) > 0, если i≠j.

Кроме того, d_ij(x) =  d_ji(x).

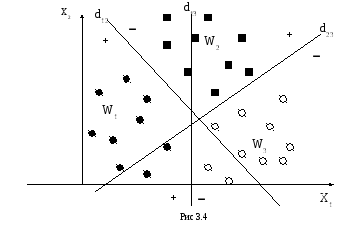
Пусть решающие функции имеют вид

d₁₂(x) = x₁x₂+5, d₁₃(x) = x₁+3, d₂₃(x) = x₁ + x₂.

Здесь области решений могут иметь несколько зон, где соответствующие функции положительны. В частности, область, отвечающая классу W₁, определяется значениями, при которых d₁₂(x) > 0 и d₁₃(x)>0. Значение функции d₂₃(x) для выделения класса W₁ роли не играет, т.к. делит классы W₂ и W₃ . Для примера рассмотрим вектор x = (4,3). Он дает d₁₂(x) = 2, d₁₃(x) = 1, d₂₃(x) = 1. Из свойства симметрии по индексам следует, что d₂₁(x) = 2, d₃₁(x) = 1, d₃₂(x) = 1. Т.к. d_3j(x)>0, объект принадлежит классу W₃.

Случай 3. Существуют M решающих функций d_k(x)=w_k`x; k = 1, 2, 3, …, M, таких, что если образ x принадлежит классу W_i, то

d_i(x)> d_j(x) для всех i≠j.

Эта ситуация – разновидность ситуации 2, т.к. можно положить, что

d_ij(x)= d_i(x)d_j(x)= (w_i w_j)`x = w_ij x.

Легко убедиться, что если d_i(x)>d_j(x) для всех i≠j, то d_ij(x)>0 для всех i≠j.

Пусть решающие функции имеют вид

d₁(x) = x₁+x₂, d₂(x) = x₁+x₂1, d₃(x) = x₂.

Разделяющие границы для трех классов выглядят при этом так:

d₁(x)  d₂(x) = 2x₁+1=0;

d₁(x) d₃(x) = x₁+ 2x₂= 0;

d₂(x)  d₃(x) = x₁+2x₂1=0.

Чтобы определить область решений для класса W₁ надо выделить область, в которой d₁(x)>d₂(x) и d₁(x)> d₃(x). Эта область совпадает с положительными зонами для прямых 2x₁+1=0 и x₁+ 2x₂= 0. В случае 3 области неопределенности отсутствуют, за исключением собственно разделяющих границ.

Нелинейные решающие функции.

d(x) = w₁ f₁(x)+w₂ f₂(x)+w₃ f₃(x)+…+ w_K f_K(x) + w_K+1= .

Классификация образов с помощью функций расстояния

Случай единственного эталона. Рассмотрим M классов; пусть эти классы допускают представление с помощью эталонных образов z₁, z₂, … z_M. Рассмотрим евклидово расстояние между произвольным вектором образа z_i и классифицируемым образом x. Оно равно

D_i = || x  z_i || = ,

где n - число координат пространства признаков.

Образ зачисляется в тот класс, для которого расстояние D_i наименьшее. Другими словами, образ x приписывается к классу W_i, если D_i < D_j для всех j ≠ i.

Этой формуле можно придать более удобный вид:

D_i² = || x  z_i ||² = (x  z_i)` (x  z_i) =

= x`x  2 x`z_i  z_i`z<sub>i</sub> = x`x  2 (x`z<sub>i</sub>  z<sub>i</sub>`z_i/2)  .

Поскольку первое слагаемое в последнем выражении не зависит от выбора эталона класса, легко видеть, что требование минимума D_i² – это требование максимума

d_i(x) = (x`z<sub>i</sub>  z<sub>i</sub>`z_i/2).

Т.е. d_i(x)  это линейная разделяющая функция с которыми мы познакомились на предыдущей лекции. Причем образ зачисляется в класс i, если d_i(x) > d_i(x) для всех j ≠ i. (случай 3).

Таким образом, классификация по признаку минимума расстояния – это классификация с помощью линейной разделяющей функции.

Случай множественного эталона. Если класс описывается несколькими эталонами («область класса» не связная, имеет более одного кластера), функция определяющая расстояние может быть записана в виде:

D_i = || x  z_i^l ||, где l = 1, 2, …, N_i

где N_i – количество эталонов класса, l – индекс по эталонам.. Следуя процедуре, рассмотренной выше, мы в качестве решающей функции будем рассматривать

d_i(x) = { (x`z<sub>i</sub><sup>l</sup>  (z<sub>i</sub><sup>l</sup>)`z_i^l / 2) }.

Как и ранее, образ x зачисляется в класс W_i, если условие

Классификация по принципу ближайшего соседа. Предположим, что у нас имеется N образов с уже известной классификацией: S = {s₁, s₂, … s_N }. Классификация по принципу ближайшего соседа состоит в том, что неизвестный образ x относится к тому или иному классу в зависимости от того, к какому классу принадлежит его ближайший сосед из набора S (1-БС-правило):

D(s_i, x) = { D(s_l, x)}, где l = 1, 2, …, N_i

Обобщением данного подходя является q-БС-правило. Согласно ему, объект x зачисляется в тот класс, к которому принадлежит большинство из q его ближайших соседей. По сути дела – это ни что иное, как распознавание при множественности эталонов, если в качестве D брать евклидово расстояние.

Байесовский классификатор. Если классификатор принимает решение о принадлежности x классу W_j тогда, как на самом деле он принадлежит классу W_i, то классификатор терпит убытки размером L_ij. Так как образ на самом деле может принадлежать любому из M классов W_i, где i = 1, … M, то математическое ожидание потерь равно

r_j = .

В теории статистических решений эту величину называют условным средним риском или условными средними потерями. Классификация осуществляется так, что образ x причисляют к тому классу, для которого r_j минимально. Такой классификатор называется байесовским. Со статистической точки зрения байесовский классификатор соответствует оптимальному качеству классификации.

Согласно формуле Байеса:

p(W_i| x) =

можно записать, что

r_j = ,

где p(x|W_i) называют функцией правдоподобия для класса W_i. Поскольку величина p(x) входит во все формулы вычисления средних потерь, мы можем ее «забыть» и записать последнее выражение, как

r_j = .

При M=2 получается:

r₁ = L₁₁ p(x|W₁) p(W₁) + L₂₁ p(x|W₂) p(W₂);

r₂ = L₁₂ p(x|W₁) p(W₁) + L₂₂ p(x|W₂) p(W₂).

Образ зачисляется в класс W₁, если r₁ < r₂ . Это то же самое, что

L₁₁ p(x|W₁) p(W₁) + L₂₁ p(x|W₂) p(W₂) < L₁₂ p(x|W₁) p(W₁) + L₂₂ p(x|W₂) p(W₂),

или

(L₁₁  L₁₂ ) p(x|W₁) p(W₁) < (L₂₂  L₂₁ ) p(x|W₂) p(W₂).

Наконец (т.к. L₁₁ < L₁₂ и L₂₂ < L₂₁),

.

Величину l₁₂(x) часто называют отношением правдоподобия, а ₁₂  пороговым значением. Образ зачисляется в класс W₁, если выполняется условие l₁₂(x) > ₁₂ и в класс W₁, если l₁₂(x) < ₁₂. В случае равенства l₁₂(x) = ₁₂ решение выбирается произвольным образом.

В случае разделения на несколько классов условие принадлежности образа x классу W_k принимает вид:

,

для всех j ≠ k.