2.4. Моделирование рассуждений на основе теории свидетельств г.Шафера

Множество окружения и фрейм различия. В этом разделе рассмотрим метод обработки неточных суждений, предложенный в 1976 г. американским математиком Г.Шафером [Shafer G. A mathematical theory of evidence, 1976]. Метод был создан на основе идей Демпстера по представлению неточных знаний на основе нескольких вероятностей вместо единственного числа и потому иногда называется методом Демпстера-Шафера.

В основу метода положено понятие окружения и основывающегося на нем понятия фрейма различия.

Теория Д.-Ш. предполагает, что имеется фиксированное множество взаимоисключающих и взаимодополняющих элементов

 = {₁, ₂, …, _N},

которое называется окружением. Понятие окружения в чем-то аналогично понятию универсума, или полной группы событий в теории вероятностей. Считается, что ничего в данный момент кроме множества  нас «не интересует», есть только окружение и ничего более.

Предположим далее, что имеется некий вопрос, на который мы желаем получить ответ. Окружение  называется фреймом различия, когда его элементы могут быть интерпретированы как ответы и только один ответ является правильным. В соответствии с теорией свидетельств предположим, что имеется некоторый вопрос, в качестве ответа на который может быть предложено N взаимоисключающих и взаимодополняющих гипотез  = {H₁, H₂, …, H_N } так, что ответом, в принципе, может быть любое из подмножеств множества . В ТДШ данное множество называют окружением.

Учитывая, что в силу возможного недостатка данных мы иногда не в состоянии выделить в качестве ответа единственный элемент из , ответом будем считать и любое подмножество `  .

В теории свидетельств с каждым из подмножеств ` связывают понятие массы m(`), которая есть ни что иное, как мера нашей уверенности в том, что данный подмножество – искомый ответ, либо как-то связано с ним (если правильный ответ H_i  `). Масса в подмножествах накапливается по мере поступления свидетельств в пользу того, что данное подмножество содержит искомый ответ и перераспределяется между подмножествами при поступлении конфликтных свидетельств (в силу того, что элементы H<sub>1</sub>, H<sub>2</sub>, …, H<sub>N</sub> взаимно исключают друг друга, конфликтуют любые два свидетельства, подкрепляющие непересекающиеся подмножества `   и ``  , где `  `` = ). Понятно, что масса всего множества  характеризует меру нашего незнания как ответить на вопрос (мы знаем лишь то, что ответ где-то среди элементов множества ). Сумма масс всех подмножеств

. (5.16)

Поскольку в общем случае m()  0 отсюда следует, что

m(`) + m(`)  1,

что и является ограничением (5.15), выраженным в терминах массы.

Масса пустого подмножества m() = 0. Нулю равны также массы всех подмножеств, по которым не поступало никаких свидетельств.

Принцип накопления и перераспределения масс на основе поступающих свидетельств определен правилом Демпстера:

m₁m₂ (Z) =,

которое мы разберем на примере. Здесь m₁m₂(Z) – комбинированная мера уверенности в подмножестве Z (масса Z), полученная на основе свидетельств 1 и 2; m₁() – масса подмножества, вычисленная на основе 1-го свидетельства, m₂() – масса подмножества, вычисленная на основе 2-го свидетельства. Расчет идет по всем парам подмножеств, пересечение которых дает Z.

Рассмотрим пример. Предположим, что у нас есть конечное множество взаимоисключающих ответов на некоторый вопрос. Например, на вопрос «Что это за самолет?» можно ответить: пассажирский лайнер (Л), бомбардировщик (Б), или истребитель (И) (для простоты предположим, что других самолетов нет). Конкретный самолет может быть либо одним, либо другим, либо третьим. Множество таких взаимоисключающих альтернатив и формирует множество окружения:

 = {Л, Б, И},

которое в данном контексте можно считать фреймом различия. Элементы Л, Б и И взаимоисключают и взаимодополняют друг друга в том смысле, что лайнер – это не бомбардировщик и не истребитель, истребитель – не лайнер и не бомбардировщик и т.д. и других самолетов нет.

Отметим также, что ответами могут быть и подмножества множества окружения. Например подмножество {Б, И} есть ответ на вопрос «Какой самолет военный?», а подмножество {Л, Б} – ответ на вопрос «Какой самолет большой?» или «Какой самолет не истребитель?». Ответом может служить и само окружение  (как свое собственное подмножество). Так {Л, Б, И} – есть ответ на вопрос «Что это?» («самолет»). Таким образом, ответами на все предполагаемые вопросы могут служить подмножества множества окружения. Т.е. все возможные ответы на все предполагаемые вопросы размещены во множестве всех подмножеств множества , которое мы обозначим Р().

Если ответа в данном окружении нет, считаем, что ответом является пустое множество .

Из теории множеств известно, что число элементов N(Р) множества всех подмножеств Р() равно 2^N(), где N() – число элементов множества . Для нашего примера это

Р() = {, Л, Б, И, {Л, Б}, {Л, И}, {Б, И}, {Л, Б, И}};

т.е. N(Р) = 2³ = 8 (пустое множество  также входит в этот перечень).

Масса подмножества и незнание. Как видим, имеется определенное сходство между теорией вероятности и теорией свидетельств. Как и в теории вероятностей мы вводим полную группу событий (окружение ) и ее подмножества – события (множество Р()). Однако в отличие от теории множеств вероятности здесь не обосновываются, например на основе результатов статистических исследований, а назначаются произвольным образом. Обычно это – наше доверие (априорное, или подкрепленное дополнительными свидетельствами) в то, что то или иное подмножество множество окружения есть ответ на поставленный вопрос. Чтобы подчеркнуть это различие, в теории свидетельств обычно говорят не о вероятности (события), а о массе (подмножества). Однако в понятии массы легко различаются черты упомянутой ранее субъективной вероятности, правда со своими особенностями, о которых пойдет речь ниже.

Основным различием между теорией Д-Ш и теорией вероятности заключается в обработке незнания. Так, в теории вероятности неполная уверенность в гипотезе А, например Р(А) = 0.7, означает уверенность в противоположной гипотезе Р(А) = 1 – 0.7 = 0.3. Это обусловлено известной взаимосвязью

Р(А) + Р(А) = 1.

Т.е. неполная уверенность в гипотезе означает частичную уверенность в ее отрицании. Теория Д-Ш недостаток уверенности не трактует никак. Мы уверены или же не уверены в гипотезе настолько, насколько эта уверенность (неуверенность) обоснована теми или иными свидетельствами. В результате вполне возможна ситуация, когда

Р(А) + Р(А)  1,

или в терминах массы:

m(А) + m(А)  1,

Масса в теории Д-Ш распределена по подмножествам множества окружения и показывает насколько то или иное подмножество может быть ответом на поставленный вопрос. Сумма масс всех подмножеств должна равняться единице:

.

Это – единственное ограничение на массы. При этом пустому множеству  всегда приписывается нулевая масса: m() = 0. Незнание (недостаток свидетельств) приписывается самому окружению . Т.е. m() – это мера нашего незнания. По мере появления новых свидетельств в пользу того или иного подмножества X  , масса m() будет убывать и в соответствии с вышеприведенным требованием единичной общей массы – распределяться по соответствующим подмножествам. Рассмотрим этот процесс подробнее.

Предположим, что нам требуется определить тип неизвестного самолета и поступило свидетельство силы 0.7 в то, что самолет – военный (силу любого свидетельства оцениваем числом из интервала [0, 1]). Это означает, что подмножеству {Б, И} следует приписать массу равную 0.7. Недостаток уверенности в том, что самолет военный, равен 0.3 и он приписывается окружению . Таким образом, имеем следующие значения масс подмножеств:

m() = 0;

m({Л}) = 0;

m({Б}) = 0;

m({И}) = 0;

m({Л, Б}) = 0;

m({Л, И}) = 0;

m({Б, И}) = 0.7;

m({Л, Б, И}) = m() = 0.3.

Нулю приравнена масса пустого множества, а также массы всех подмножеств для которых не поступило свидетельств (в т.ч. и подмножеств {Б} и {И}, поскольку свидетельство поступило в пользу {Б, И}, а не какого-то из них в отдельности). Легко видеть, что требование единичной общей массы здесь сохраняется.

Каждое подмножество множества окружения с ненулевой массой называется центральным (или фокальным) элементом. В данном случае центральными элементом является подмножество {Б, И}.

Разберем процедуру перераспределения исходной массы в связи появлением новых свидетельств.

Комбинирование свидетельств. В теории вероятностей влияние вновь поступающих свидетельств на апостериорную вероятность случайного события оценивается с помощью теоремы Байеса. Для этого следует знать априорные вероятности, что не всегда возможно. В теории свидетельств учет новой информации производиться на основании правила комбинирования свидетельств Демпстера. Рассмотрим его, продолжая наш пример.

Пусть дополнительно к первому свидетельству о том, что самолет военный поступило уточняющее свидетельство силы 0.9, что это – бомбардировщик. Массы свидетельств теперь будут следующими: m₁({Б, И}) = 0.7, m₁() = 0.3, а также m₂({Б}) = 0.9, m₂() = 0.1. Требуется определить комбинированную массу подмножеств, учитывающую оба этих свидетельства. Здесь m₁ и m₂ относятся к первому и второму свидетельству соответственно. Комбинирование осуществим по ранее упомянутому правилу Демпстера:

m₁ m₂(Z) =.

Т.е. комбинированная масса подмножества Z равно сумме произведений масс всех подмножеств, пересечение которых дает подмножество Z.

Для удобства выпишем в таблицу значения масс всех подмножеств в пользу которых поступили свидетельства (т.е. все ненулевые массы). Строки соответствуют первому, а столбцы – второму свидетельству. На пересечениях строк стоят пересечения данных подмножеств и произведение их масс:

	m2({Б}) = 0.9	m2() = 0.1
m1({Б, И}) = 0.7	m1m2({Б}) = 0.7  0.9	m1m2({Б, И}) = 0.7  0.1
m1() = 0.3	m1m2({Б}) = 0.3  0.9	m2() = 0.3  0.1

В результате комбинирования получаем новые массы:

m₁ m₂() = 0;

m₁ m₂({Л}) = 0;

m₁ m₂({Б}) = 0.63 + 0.27 = 0.9;

m₁ m₂({И}) = 0;

m₁ m₂({Л, Б}) = 0;

m₁ m₂({Л, И}) = 0;

m₁ m₂({Б, И}) = 0.07;

m₁ m₂() = 0.03.

Как видим, доверие в то, что это просто «военный самолет» убыло и появилось значительное доверие к тому, что это – бомбардировщик (знание стало более точным). Подмножество {Б} также стало центральным элементом наряду с {Б, И}. Убыло и незнание (масса окружения).

Теперь предположим, что поступило конфликтное свидетельство силы 0.95, что самолет – пассажирский лайнер. Оно явно противоречит первым двум. Разберем как теория свидетельств обрабатывает конфликтующие свидетельства.

Имеем m₃({Л}) = 0.95; соответственно, m₃({} = 0.05. Строим таблицу аналогичную предыдущей.

	m3({Л}) = 0.95	m3() = 0.05
m1 m2({Б}) = 0.9	 0.855	m1 m2 m3{Б}= 0.045
m1 m2({Б, И}) = 0.07	 0.0665	m1 m2 m3{Б, И}= 0.035
m1 m2() = 0.03	m1 m2 m3{Л}= 0.0285	m1 m2 m3() = 0.0015

Пустое множество в клетках показывает, что пересечение соответствующих подмножеств – пустое множество.

Особенностью здесь является то, что часть массы «оттянуло» на себя пустое множество , массу которого мы априори принимаем равной 0. В результате возникает вопрос перераспределения массы, приписанной в таблице пустому множеству, по остальным подмножествам множества . Для этого в теории Д-Ш предусмотрена процедура нормализации массы. Нормализация осуществляется путем деления масс центральных элементов на величину

K = ,

которая в данном случае есть K = 1  (0.855 + 0.0665) = 0.0785. В итоге получаем:

m₁ m₂ m₃() = 0;

m₁ m₂ m₃({Л}) = 0.363;

m₁ m₂ m₃({Б}) = 0.573;

m₁ m₂ m₃({И}) = 0;

m₁ m₂ m₃({Л, Б}) = 0;

m₁ m₂ m₃({Л, И}) = 0;

m₁ m₂ m₃({Б, И}) = 0.045;

m₁ m₂ m₃() = 0.019.

Как видим, конфликтное свидетельство уменьшило нашу уверенность в том, что самолет военный и что самолет  бомбардировщик, и это вполне разумно. Зато появилось доверие в авиалайнер.

Таким образом, окончательно общий вид правила комбинирования масс можно записать в виде:

m₁ m₂(Z) =.

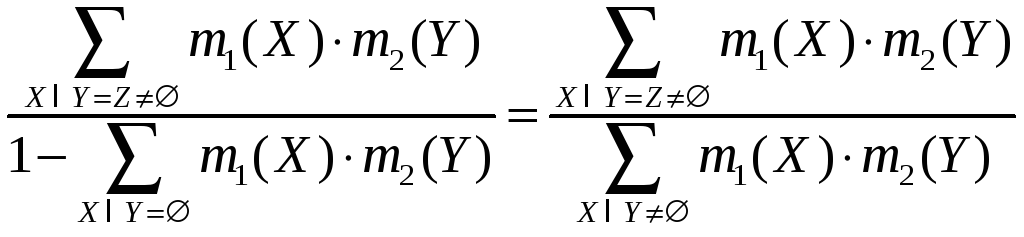Функция доверия и интервал свидетельств. Основные функции теории Шафера. Значение m(X), где Х характеризует уверенность в том, что подмножество Х является ответом на поставленный вопрос. Но Х может содержать в себе подмножества, которые, таким образом, также являются ответом. Так множество {Б, И} в качестве подмножества содержит множество {Б}. Общее доверие в множество {Б, И} состоит из доверия собственно в {Б, И} плюс доверие в {Б}, как его подмножество (других подмножеств, являющихся центральными элементами здесь нет). Чтобы учесть подобные обстоятельства в теории свидетельств вводят т.н. функцию доверия

Bel(Y) =.

Эта функция определяет нижнюю границу нашей уверенности в том, что Y есть ответ. В рассматриваемом случае

Bel({Б, И}) = m({Б, И}) + m({Б}) = 0.045 + 0.573 = 0.618.

Действительно, бомбардировщик – это военный самолет, а значит доверие к ответу «военный самолет» включает в себя и ответ «бомбардировщик».

Поскольку функция доверия есть простая сумма масс подмножеств, комбинированное доверие, обусловленное несколькими свидетельствами, вычисляется через комбинирование масс, как это делалось выше:

Bel₁ Bel₂(Y) =.

В частности,

Bel₁ Bel₂({Б, И}) = m₁ m₂({Б, И})+ m₁ m₂({Б}) + m₁ m₂({И})

(пустое множество, масса которого всегда равна нулю, можно не записывать).

Как и в обычном вероятностном выводе помимо нижней границы истинности, которая здесь задается функцией доверия, можно определять и верхнюю границу. Верхняя граница доверия к множеству Y определяется по формуле

Pls(Y) = 1  Bel(Y),

где Bel(Y)  доверие к множеству, дополняющему Y до . Функция Pls(Y) называется правдоподобием.

В случае множества Y = {Б, И}, дополнение Y есть множество {Л}. Тогда

Pls(Y) = 1  Bel({Л}) = 1  m({Л}) = 1  0.363 = 0.637.

Истинное доверие к Y лежит в интервале EI(Y) = [Bel(Y), Pls(Y)]. Для нашего случая это EI({Б, И}) = [0.618, 0.637].

Нижняя граница веры в Y, определяемая функцией Bel(Y) называется базой, а верхняя (определяемая Pls) – правдоподобием. Всегда выполняется условие

0  Bel(Y)  Pls(Y)  1.

На основе функций правдоподобия и доверия в теории свидетельств вводятся также функции сомнения Dbt(Y) и незнания Igr(Y):

Dbt(Y) = Bel(Y) = 1  Pls(Y);

Igr(Y) = Pls(Y)  Bel(Y).