2.3. Вероятностные модели правдоподобных рассуждений

Вероятность и правдоподобные рассуждения. Одно из основных достоинств использования вероятностных моделей в автоматизированных схемах рассуждений заключается в возможности обрабатывать противоречивые суждения посредством достаточно сложившегося и обоснованного математического аппарата теории вероятностей.

Традиционно рассматриваются несколько подходов к определению вероятности.

1. «Классическое» определение вероятности как отношение числа благоприятных исходов для какого-либо события N_благ(А) к общему числу возможных событий N_общ [Б.Паскаль, П. Ферма]

Р(A) = N_благ(А)/ N_общ.

Например, вероятность выпадения четного числа очков на игральной кости равно отношению 3 (число граней с четными очками) к 6 (общее число граней): 3/6 = 0.5.

2. «Статистическое» определение вероятности как предел отношения числа благоприятных исходов опыта M_благ(А) к общему числу проделанных опытов M_общ при условии, что число проделанных опытов M_общ стремиться к бесконечности:

Р(A) = M_благ(А)/ M_общ, при M_общ

Этот взгляд на вероятность наиболее широкое распространение получил в XIX веке [Дж.Венн - 1892].

3. «Субъективное» определение вероятности. В такой трактовке вероятность – это просто наша субъективная мера уверенности в том, что случайное событие А произойдет (например при очередном опыте). Например, когда мы говорим, что вероятность выпадения четной грани игрального кубика равна 0.5, мы даем субъективную оценку возможности осуществления этого события. Действительно, реальный игральный кубик не симметричен, для него вряд ли можно говорить, что вероятность здесь будет в точности 0.5. Скорее всего она будет несколько отличаться от 0.5. Однако насколько – мы никогда не узнаем, поскольку для этого следует произвести бесконечное число опытов, что невозможно.

Данная трактовка вероятности восходит, в частности, к американским математикам и статистикам XX века [Д.М.Кейнс - 1921, Ф.П.Рамсей - 1931].

4. Наконец в первой половине XX века зародился также аксиоматический подход к вероятности, основоположником которого стал советский математик А.Н.Колмогоров [1936]. В основе этого подхода лежит представление о том, что вероятность – это некое число, связанное с тем или иным подмножеством т.н. «полной группы событий» и удовлетворяющее специальному набору аксиом. Этот подход считается на сегодня наиболее строгим.

Моделирование правдоподобных рассуждений с помощью вероятности. Как видим, одна из трактовок понятия вероятности – а именно третья  оказывается достаточно широкой, чтобы рассматривать вероятность не просто как статистическую величину, проявляющуюся только в большом числе опытов, а как некую субъективную меру уверенности в чем-то. В этом смысле она близка фактору уверенности для неточного вывода, или лучше сказать – нечеткому понятию истинности, если последнюю рассматривать как точку на интервале [0,1]. Если при этом мы дополним такой взгляд на истинность аксиомами, аналогичными аксиомам вероятности, аналогия между истинностью и вероятностью становится еще более глубокой. Именно эта аналогия и стала основой для использования вероятностных методов в неточных рассуждениях

Согласно этому подходу истинность некоторого суждения А задается величиной Р(А) – «вероятностью» того, что А есть Истина. Соответственно Р(А) – вероятность отрицания события А – это «вероятность того, что А – Ложь. Согласно свойствам вероятности справедливо точное равенство:

Р(А) + Р(А) = 1.

Это равенство является основой для определения истинности отрицания суждения в такой логике:

Р(А) = 1  Р(А).

Истинность импликации при таком выводе может задаваться как условная вероятность события А при условии, что произошло событие В: Р(А|В).

Если А и В два взаимно независимых события (суждения) истинность их конъюнкции и дизъюнкции можно вычислять по формулам:

Р(А&В) = Р(А) Р(В);

Р(АВ) = Р(А) + Р(В)  Р(А) Р(В),

 в полном соответствии с теорией вероятности.

Аналогом вывода по правилу modus ponens может служить вычисление Р(В) по формуле:

Р(В) = Р(В|А) Р(А).

Легко заметить, что в последнем случае мы на самом деле вычисляем не вероятность («истинность») события (суждения) В, а вероятность произведения двух случайных событий Р(АВ) (суждения А&В). Истинная вероятность события В, которую мы в точности не знаем, больше чем вычисленная по вышеприведенной формуле. Расчет по последней формуле дает только некий «гарантированный минимум» вероятности Р(В), т.к. справедливо неравенство Р(АВ)  Р(В). Обозначим этот минимум как Р_min(В). Итак, Р_min(В) = Р(В|А)Р(А).

Кроме гарантированного минимума мы можем рассчитать также и «гарантированный максимум» вероятности (истинности) В. Для этого определим гарантированный минимум отрицания В:

Р_min(В) = Р(В|А) Р(А)

и учтем, что

Р_max(В) = 1  Р_min(В).

С учетом этого, а также того, что Р(В|А) = 1  Р(В|А) получаем:

Р_max(В) = 1  Р(В|А) Р(А) = 1  Р(А) + Р(В|А) Р(А) = Р(А) + Р_min(В).

Искомое и, вообще говоря, неизвестное нам значение Р(В) лежит в интервале [Р_min(В), Р_max(В)], или, что то же самое, [Р_min(В), 1  Р(А) + Р_min(В)]. Аппроксимировать приближенно его можно средним арифметическим:

Р_са(В) = (Р_min(В) + Р_max(В))/2 = Р_min(В) + (1  Р(А)/2.

или средним геометрическим:

Р_сг(В) = = .

Оценка по среднему геометрическому может оказаться предпочтительнее в том смысле, что при точной ложности посылки: Р(А) = 0 мы имеем точно ложное заключение: Р_сг(В) = 0. Это позволяет удалять из процедуры вывода заключения из ложных посылок. При среднеарифметическом же мы в этом случае получаем значение Р_са(В) = 0.5  неопределенную ситуацию, когда нельзя склониться ни в сторону принятия ни в сторону отказа от заключения В (хотя по-своему это тоже достаточно показательно). Похожий вывод выполняется в ЭС INFERNO.

Еще одним приемом, позволяющим уточнить истинность заключения является использование условной вероятности Р(В|А), значение которой задается отдельно. Т.е. мы помимо вывода

Р₁(В) = Р(В|А) Р(А).

рассматриваем также вывод

Р₂(В) = Р(В|А) Р(А).

и считаем, что

Р(В) = Р₁(В) + Р₂(В) = Р(В|А) Р(А) + Р(В|А) Р(А),

или, что то же самое,

Р(В) = Р(В|А) Р(А) + Р(В|А)(1  Р(А)).

Последнее выражение, вообще говоря, может дать точное значение Р(В), т.к. данная сумма – это ни что иное, как истинность утверждения (В&А)(В&А), логически эквивалентного В. Однако для этого нам нужно точно знать условные вероятности Р(В|А) и Р(В|А), что не всегда возможно, особенно если речь идет о предметных областях с недостаточной статистикой. Трудность использования второго подхода заключается и в том, что условные вероятности Р(В|А) и Р(В|А) экспертами рассматриваются как взаимозависимые. Но получаемые на их основе вероятности Р₁(В) и Р₂(В) должны удовлетворять неравенству Р₁(В) + Р₂(В)  1. Это означает ограничение на свободу выбора Р(В|А) и Р(В|А). Если данное неравенство нарушается, система правил оказывается «несовместной» («противоречивой»). В общем случае (когда Р₁(В) + Р₂(В)  1) при применении этого метода истинное значение Р(В) также оказывается заключенным в интервале: [Р₁(В), 1  Р₂(В)].

Условная вероятность Р(В|А) в подобных системах задается либо непосредственно на основе экспертных оценок, либо по теореме Байеса:

Р(В|А) =

Второй вариант используется, если известны вероятности Р(А|В), Р(В) и Р(А). Например, для медицинской экспертной системы, диагностирующей болезни на основе симптомов, это может выглядеть следующим образом.

Пусть имеется ряд болезней, на распознавание которых настроена ЭС и некие симптомы на основании которых происходит постановка диагноза. Обозначим произвольную болезнь как В_i, а конкретный симптом как A. В ЭС вносится правило AВ_i (т.е. если обнаружен симптом А, то это болезнь В_i). Истинность этого правила есть условная вероятность Р(В_i|А). Поскольку болезней с одинаковыми симптомами (например головная боль, повышенная температура и т.п.) может быть много, подобных правил в системе может также оказаться много. Возникает вопрос, как расставить факторы уверенности для каждого из правил.

Согласно теореме Байеса условная вероятность P(В_i|А) (иногда ее называют апостериорной вероятностью) равна:

P(В_i|А) =

или в несколько иной форме:

P(В_i| А) = .

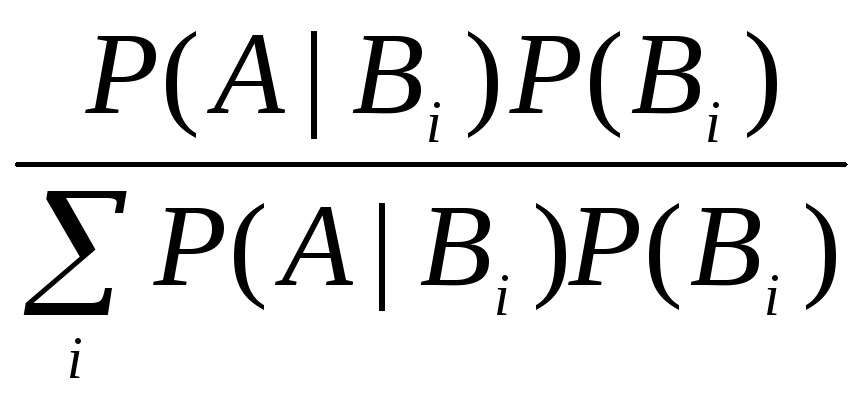Здесь учтено, что согласно формуле полной вероятности

P(А) = ,

где суммирование происходит по всем гипотезам (диагностируемым болезням). Но вероятности P(В_i) и условные вероятности P(A|В_i) – это, соответственно, вероятности (т.е. относительная частота появлений, встречаемость) болезней В_i и вероятность встретить симптомы A при условии того, что пациент болен болезнью В_i. Все эти вероятности могут быть получены из медицинской статистики. Учитывая их мы можем рассчитать и вероятности (истинности) P(В_i| А) для каждого из правил AВ_i.

Теорема Байеса может использоваться и иначе. В базу знаний заносят априорную вероятность осуществления проверяемой гипотезы: P(B) и условные вероятности P(A | B) и P(A | B) – вероятности обнаружить «симптом» в случае наличия и отсутствия «болезни» B (для медицинской ЭС они м.б. получены на основе соответствующей статистики). Далее, при обнаружении симптома A вычисляют истинность гипотезы B по одной из форм теоремы Байеса:

,

как апостериорную вероятность, полученную после обнаружения симптома A. В случае получения нового симптома, в качестве априорной берется апостериорная вероятность, вычисленная на первом шаге (симптомы считаются независимыми). Вероятность осуществления некой гипотезы B при наличии определенных подтверждающих свидетельств A вычисляется на основе априорной вероятности этой гипотезы без подтверждающих свидетельств и вероятностей осуществления свидетельств при условиях, что гипотеза верна или неверна. Такой тип вывода называют байесовским выводом.

В соответствующих базах знаний такой вывод предполагает хранение как минимум трех числовых значений: априорной («стартовой») вероятности P(B), условной вероятности P(B|A) и условной вероятности P(B|A). Каждый новый «симптом» добавляет еще пару значений P(B|A_i), P(B|A_i). Он очень похож на алгоритм байесовской классификации, который мы рассмотрим позже в теории распознавания образов.

Моделирование на основе понятия шанса. Оригинальный подход к моделированию правдоподобных рассуждений реализован в известной ЭС PROSPECTOR. Как и в только что рассмотренном варианте он основан на байесовском выводе, но неопределенность знаний в нем формализуется не вероятностью, а шансом.

Шансом (odds) О(А) события А называется отношение вероятностей Р(А) и Р(А):

О(А) = = .

И наоборот

Р(А) = .

Т.е. «шансы» = «шансы за» / «шансы против». Легко заметить, что шанс осуществления достоверного события стремиться к бесконечности, а невозможного – к нулю.

Условная вероятность в терминах шансов рассматривается как условный шанс О(В|А) осуществления события В при условии события А. Условный шанс связан с условной вероятностью по формуле:

О(В|А) = .

Учитывая, что по теореме Байеса

P(В|А) =

а также

P(В|А) =

на основе априорного шанса O(B) можно рассчитать апостериорные шансы:

О(В|А) = = О(В) = LS(А)О(В)

Отношение LS(А) = называется фактором достаточности. Он становится бесконечно большим, когда Р(А|В)  0, т.е., когда отсутствие события В делает невозможным событие А, или, что то же самое, А достаточно для В. С другой стороны он равен 0, когда Р(А|В) = 0, т.е., когда наличие В делает невозможным А. Но это то же самое, что наличие В делает невозможным А т.к. множества событий А и В в этом случае не пересекаются.

Случай LS = 1 означает равенство Р(А|В) = Р(А|В). Событие А в этом случае не влияет на событие В (в том числе – не является его причиной).

В целом можно заключить, что событие А благоприятно для В, если фактор 1< LS < , неблагоприятно, если 0< LS < 1 и нейтрально, при LS = 1. Случай LS   означает, что событие В при наличии А безусловно истинно.

В случае конъюнкции нескольких взаимонезависимых причин фактор достаточности можно рассчитать как произведение факторов. Например, LS(А₁&А₂) = LS(А₁)LS(А₂). Действительно,

LS(А₁&А₂) = = = LS(А₁)LS(А₂).

Наряду с фактором достаточности в подобных системах рассматривают также фактор необходимости, который вычисляется как

LN(А) = .

Или в более развернутой форме:

О(В|А) = = О(В) = LN(А)О(В)

Содержательно фактор необходимости показывает насколько причина А необходима для заключения В. Так при Р(А|В)  0 отсутствие А благоприятно для В (LN  ), а значит он не является необходимым для В (более того – «препятствует» В). Наоборот, при Р(А|В) = 0 получаем значение LN = 0. Т.е. А безусловно необходимо для В. Наконец при LN(А) = 1 событие А не влияет на событие В.

Фактор LS(А) показывает насколько меняются шансы встретить событие В с появлением события А, а фактор LN(А) – насколько эти шансы меняются, если событие А не зарегистрировано.

Факторы необходимости и достаточности связаны друг с другом. Действительно, запишем LN(А) в виде:

LN(А) = = .

Видно, что если LS(А) > 1, то, поскольку при этом Р(А|В) > Р(А|В), справедливо строгое неравенство LN(А) < 1. И наоборот, в случае, когда Р(А|В) < Р(А|В) получаем, что LN(А) > 1. Наконец при Р(А|В) = Р(А|В) вместе равны единице: LS(А) = LN(А) = 1. Эту связь можно выразить и так:

Р(А|B) LN(А) + Р(А|B) LS(А) = 1.

Поскольку значения факторов LS(А) и LN(А) задаются экспертами, они должны учитывать эту взаимосвязь (ср. с требованием взаимосвязанности условных вероятностей Р(В|А) и Р(В|А), упомянутым ранее).

В заключение интересно отметить, что моделирование конъюнкции и дизъюнкции суждений в системе PROSPECTOR осуществляется с помощью операция минимума и максимума двух вероятностей:

Р(А&B) = min(P(А), Р(B));

Р(АB) = max(P(А), Р(B)),

как в т.н. нечетких логиках, с которыми мы познакомимся позже.

Достоинства и ограничения вероятностных моделей. Достоинством вероятностных моделей логических рассуждений является использование широко апробированного и положительно зарекомендовавшего себя аппарата теории вероятности. Однако недостатком здесь служит то, что такие модели все же наиболее эффективны для предметных областей с богатым статистическим материалом. Например, медицина, социология, геология, некоторые естественные науки. Если статистического материала нет, мы в принципе можем вспомнить о субъективной трактовке вероятности, но целесообразность применения аппарата теории вероятностей в этом случае становиться менее очевидной. Вероятностной точке зрения на истинность, а также соответствующим вероятностным логикам здесь приходится конкурировать с другими, возможно более эффективными логическими моделями.

Вторым недостатком теории вероятности, в случае применения ее в целях логического вывода на реальных предметных областях, можно считать жестко обусловленную связь

Р(А) + Р(А) = 1.

Она означает, что всякий недостаток уверенности в истинности А следует трактовать истинность отрицания А. К сожалению, мы не всегда можем быть в этом уверены. Иной подход к взаимосвязи утверждения и отрицания, допускающий отсутствие или недостаток как аргументов «за» так и аргументов «против» принят в теории свидетельств Г. Шафера, который мы разберем ниже. В известном смысле теорию Шафера можно рассматривать как обобщение теории вероятностей. Причем вероятность в ней трактуется, вообще говоря, субъективным образом.