Моделирование нечетких знаний

Сначала определим, что такое неопределенность. Неопределенность бывает 2 видов (рис. 1):

• недостоверность

• неоднозначность

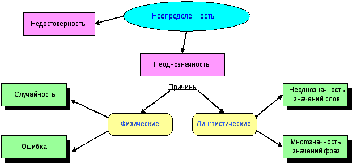Рис.1. Неопределенность и ее причины

Недостоверность характеризуется тем, что процессы полностью не изучены, или изучены недостаточно. Недостоверность уменьшается по мере изучения процесса.

Неоднозначность характеризуется тем, что задача изучена, но нет возможности четко представить ее описание.

Неоднозначность имеет физические и лингвистические причины.

Физические причины – это результат влияния внешней среды.

Лингвистические причины связаны с особенностями естественного языка.

Существует множество методов устранения неопределенности, основным из которых является теория нечетких множеств.

Нечеткие множества

Пусть Х – множество некоторых объектов х, соответствующих некоторому понятию: Х={х} называют универсальным множеством. Нечетким (расплывчатым) множеством А, соответствующим заданному понятию, назовем множество пар А = {< _А(х) / х>}, где х  Х, а _А(х) - функция принадлежности (степень принадлежности), _А(х)  [0,1].

_А(х) - субъективная мера того, насколько элемент х множества Х соответствует понятию, формализуемому с помощью нечеткого множества А. Если множество Х представить как множество действительных чисел, получим непрерывную функцию принадлежности.

S_A={x | xX & _А(х)>0} – носитель нечеткого множества.

ПРИМЕР. Имеется универсальное множество X={5,10,15,…,40}, соответствующее понятию детский возраст. Найдем нечеткое множество и построим функцию принадлежности.

А={<1/5>, <1/10>, <0,6/15>, <0,3/20>, <0/25>, <0/30>, <0/35>, <0/40>}.

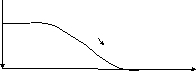
Графическое представление функции принадлежности показано на рис.2.

1 _А(х)

функция

принадлежности

5 10 15 20 25 30 35 40 x

Рис.2. Пример построения функции принадлежности.

Если Х – непрерывно, то переходим к непрерывному варианту и получаем функцию принадлежности.

В большинстве случаев функции принадлежности строятся субъективно по результатам опроса экспертов, поэтому они являются в некотором смысле «приближенными», т.е. не абсолютно адекватно отражающими явление или объект. Собственно говоря, из субъективности следует, что абсолютной адекватности не существует в принципе. Поэтому, нужно выбирать такую функцию, с которой можно было бы как можно проще вести расчеты. Такими функциями являются трапециевидные функции (рис.3). Тогда _А(u) характеризуется четверкой (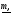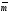,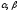). Как частный случай при 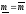имеем треугольную форму трапеции.

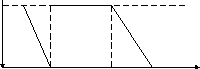
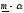
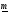
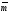
_А(u)

u

Рис.3. Трапециевидная функция принадлежности

Операции над нечеткими множествами

Пусть имеем нечеткие множества А и В на универсальном множестве Х с функциями принадлежности _А(х) и _В(х).

1. Дополнение – это нечеткое множество с функцией принадлежности



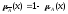
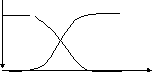
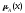
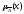
х

Рис.4. Операция дополнения

2. Объединение – это нечеткое множество с функцией принадлежности

_АB(х)=max(_А(х), _В (х)), хХ.



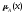
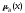_АB(х)

х

Рис.5. Операция объединения

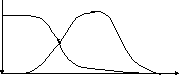
3. Пересечение – это нечеткое множество с функцией принадлежности

_АB(х)=min(_А(х), _В(х)), хХ.



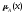
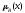
_АB(х)

х

Рис.6. Операция пересечения

4. Импликация – это нечеткое множество с функцией принадлежности

_{А B}(х)=max(1-_А(х), _В(х)), хХ.

5. Степень включения множества А в В – это величина ( А, В ):

( А, В )= (_А(х) _B(х)).





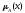
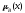
х

Рис.7. Степень включения

Здесь результат операции & понимается как минимум значений функции.

В логике Заде: (_А(х) _B(х)= (1-_А(х)) _B(х).

( А, В )=min (max(1-_А(х), _B(х)).

В логике Лукасевича : _А(х) _B(х)=1(1-_А(х)+ _B(х)).

Очевидно, если А В, то ( А, В )=1, если А В ( А, В )=0.

6. Степень равенства

_А,B(х)=&(_А(х) _В(х))=&[ (_А(х) _B(х))&( _B(х) _A(х))], хХ.