68.Відокремлені і відокремлюванні зміні.

Означення. ДР виду

(13)

називається ДР з відокремленими змінними. Загальний розв’язок ДР знаходимо з рівняння

Розв’язок задачі Коші з початковими умовами х = х₀, у = у₀ має вигляд

Знаходження розв’язку ДР з відокремленими змінними зводиться до квадратур, тобто до пошуку інтегралів від відомих функцій.Означення. ДР виду

N₁(y)M₁(x)dx + M₂(x)N₂(y)dy = 0 (14)

називається ДР з відокремлюваними змінними, тобто таким, що зводиться до ДР з відокремленими змінними.

Поділимо рівняння (14) на функцію N₁(y)M₂(x) і дістанемо ДР з відокремленими змінними

яке має інтеграл

ДР (14) також має розв’язки у = у_k, x = x_j, де у = у_k є коренем рівняння N₁(y) = 0, а x = x_j є коренем рівняння M₂(x) = 0 (особливі розв’язки).

Аналогічно, ДР виду

y = f(x)g(y)

є ДР з відокремлюваними змінними.

Рівняння (15) можна записати у вигляді

Рівняння (15) має також розв’язок у = у_k, де g(у_k) = 0.

69. Однорідні ДР 1 порядку

ДР називається однорідним, якщо його можна подати у вигляді

(16)

ДР (16) за допомогою заміни змінної у

зводиться до ДР з відокремлюваними змінними

і пошук розв’язку зводиться до квадратур

70..Лінійні ДР 1-го порядку.

Означення. ДР виду

(22)

де р(х), q(x) відомі функції, називається лінійним ДР. Якщо q(x)  0, то ДР називається однорідним. Якщо q(x)  0, то ДР називається неоднорідним.Однорідне лінійне ДР завжди інтегрується в квадратурах як ДР з відокремлюваними змінними:

71. Рівняння Бернуллі.

Означення. ДР виду

називається ДР Бернуллі.

Рівняння Бернуллі зводиться до лінійного ДР за допомогою заміни

55. Властивості чр

Теорема 1. Якщо збігається ряд, то збігається його залишок; і навпаки, із збіжності залишку випливає збіжність ряду.Наслідок 1. Із розбіжності ряду випливає розбіжність його залишку, і навпаки. Наслідок 2. Якщо відкинути скінченну кількість перших членів ряду або додати до нього кілька нових членів, то це не вплине на його збіжність.Теорема 2. Якщо члени збіжного ряду помножити на сталий множник с, то його збіжність не порушиться, а сума помножиться на це число с:

.

Теорема 3. Збіжні ряди і можна почленно додавати або віднімати, при цьому ряд також збігається, а його сума буде .

Теорема 4. Послідовність частинних сум збіжного ряду обмежена. Це твердження випливає зі збіжності послідовності частинних сум ряду.

Теорема 5. Якщо ряд збігається, то границя його загального члена прямує до 0, тобто: .

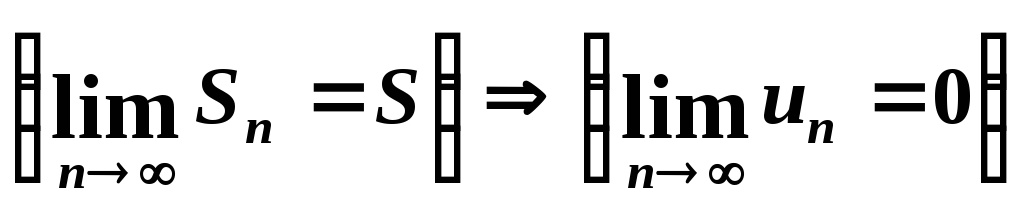Наслідок. Якщо , тобто необхідна умова збіжності ряду не виконується, то ряд розбігається.

61. Знакопочергові ряди. Означення. Ряд, кожний член якого відрізняється знаком від попереднього, називається знакопочерговим. Цей ряд має вигляд:

(9.9)

Загальний член ряду (9.9) де . Теорема 13 (Лейбніца). Якщо члени знакопочергового ряду спадають за абсолютною величиною і границя абсо- лютної величини загального члена ряду дорівнює нулю, то ряд збігається. Коротко цю теорему можна записати так:

Наслідок 1. Знак суми збіжного знакопочергового ряду такий само, як і знак першого члена ряду.Наслідок 2. Якщо знакопочерговий ряд збігається, то його сума за абсолютною величиною не перевищує першого члена ряду, тобто Наслідок 3. Якщо при обчисленні суми збіжного знакопочергового ряду обмежитись тільки першими n членами, а всі інші відкинути, то похибка за абсолютною величиною не перевищить першого із відкинутих членів, тобто . Наслідок 4. Якщо для ряду не виконується умова теореми Лейбніца , то ряд розбігається (не виконується необхідна умова збіжності).