Свободное движение частиц в неньютоновской (бингамовской) жидкости

Такие среды обладают предельным напряжением сдвига τ₀.

Для шарообразной частицы, находящейся во взвешенном состоянии, движущая сила веса равна вертикальной составляющей напряжений на ее поверхности

, (7)

откуда диаметр самой крупной частицы, остающейся во взвешенном состоянии

(8)

В действительности распределение касательных напряжений на поверхности шара неравномерно, поэтому Шищенко предложил применять экспериментальный коэффициент т, значение которого зависит от диаметра

(9)

Соотношение (9) можно использовать для оценки взвешивающей способности бурового раствора, оставленного в состоянии покоя. При циркуляции бурового раствора в скважине частицы, диаметр которых равен или меньше диаметра (9), выносятся на поверхность со скоростью движения бурового раствора. Внутри бессдвигового ядра течения увлекаемые частицы могут иметь больший диаметр, чем диаметр частицы в остальной части проходного сечения, поскольку величина обычно больше .

Для неподвижных тиксотропных жидкостей вместо τ₀ следует использовать статическое напряжение сдвига θ (определяется на приборе СНС-2 при частоте вращения 0,2 об/мин).

Движение частиц в тиксотропных жидкостях весьма сложно, поскольку в определение Re надо вводить эффективную вязкость μ_эф в окрестности частицы.

(10)

τ и распределены неравномерно по поверхности частицы, что и создает трудности.

Шищенко экспериментальным путем определил, что при a<3 режим обтекания ламинарный; при – переходный, при a>7 – турбулентный (, где d – диаметр частицы; d₀ – диаметр наибольшей частицы, остающейся во взвешенном состоянии).

В ламинарном режиме

, (11)

где ψ(a) – экспериментальная функция

В переходном и турбулентном режимах w определяется по формуле Риттингера, в которой коэффициент сопротивления зависит от формы частицы и параметра a.

Значение коэффициента можно найти из графика.

Ламинарное течение

Допущения: среда несжимаемая; движение установившееся, равномерное; течение параллельно оси трубы; среда прилипает к стенкам; труба имеет достаточную длину (нет концевых эффектов); единственные массовые силы – гравитационные.

1. Бингамовские жидкости.

Распределение скоростей в поперечном сечении потока . P – градиент давления, Па/м.

(1)

Уравнение (1) справедливо только в области, где .

Рисунок. Распределение скоростей, напряжений и скоростей сдвига при ламинарном течении бингамовских жидкостей в круглой трубе.

В потоке есть зона течения (ядро), в которой жидкость перемещается как твердое тело . Внутри ядра .

Распределение напряжений

(2)

Напряжения отрицательны, т.е. действуют в направлении, обратном направлению течения. Обычно в расчетах знак не учитывают.

Для существования течения должно выполняться условие , т.е.

(3)

Из условия неразрывности скорости потока скорость движения ядра

, (4)

или

τ_с – напряжение сдвига на стенке канала.

На рисунке наглядно показано влияние предельного напряжения сдвига на профиль скорости течения при определенном напряжении сдвига на стенке при ламинарном течении.

Объемный расход Q через трубу под действием градиента давления P

(5)

Если градиент давления, необходимый для начала течения, обозначить как (6)

то (5) можно представить в виде

(7)

Формула (7) получена Букингамом в 1921г. Представляет собой обобщение уравнения Гагена-Пуазейля, которое применяется для ньютоновских жидкостей (τ₀=0)

(8)

Напряжение сдвига на стенке трубы

(9)

С учетом (9) выражение (7) можно записать по-другому (τ_с вводится по абсолютному значению)

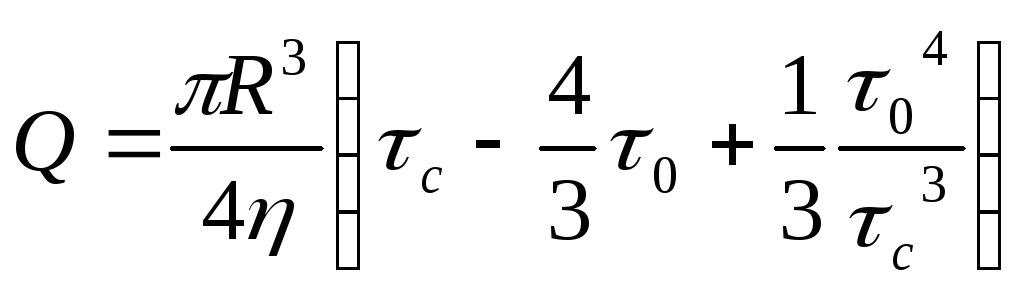(10)

Если ввести среднюю скорость потока _ср и диаметр трубы D, получим

(11)

Величина называется средней скоростью сдвига или кажущейся (номинальной) скоростью сдвига на стенке. Она равна скорости деформации жидкости вблизи стенки только для ньютоновских сред, когда величина в скобках (11) равна 1.

Сопоставляя (11) с (8), можно получить

(12)

Для больших P Бингам предположил, что , имеет место вязкопластичное течение по всему сечению трубы, т.е. жесткое ядро отсутствует. Тогда

, (13)

или (14)

Выражение в скобках в уравнении (13) отличается от аналогичного в уравнении (7) лишь отсутствием последнего слагаемого, которым можно пренебречь, если (или ).

В то же время, уравнения (12) и (14) позволяют определить эффективную вязкость бингамовских жидкостей

(15)

При бурении, как правило, требуется определять градиенты давления P (или полное давление P·l) по известному расходу Q. Однако, уравнение (7) трудно решать относительно P.

Было введено понятие коэффициента гидравлического сопротивления (безразмерный!)

, (16)

откуда

, Па/м (17)

Эта зависимость называется формулой Дарси-Вейсбаха (домножив на l, получим давление в Па).

Безразмерный коэффициент λ есть учетверенное значение соотношения между напряжением сдвига на стенке и кинетической энергией потока, приходящейся на единицу объема.

Коэффициент λ является функцией безразмерных критериев:

• критерия Рейнольдса (для бингамовских жидкостей)

(18)

• критерия Бингама (Сен-Венана) (критерий пластичности)

(19)

При использовании параметров Рейнольдса и Бингама

(20)

а также уравнения Букингама соотношение

(21)

можно выразить только через безразмерные величины

. (22)

Это уравнение может быть представлено графически в виде зависимости от Re и В в качестве параметров.

Часто используется и третья безразмерная комбинация параметров, предложенная Хедстремом:

. (23)

Уравнение (22) в этом случае принимает следующий вид:

. (24)

Для ньютоновских жидкостей В=Не=0, и уравнения сводятся к формуле Стокса

. (25)

Строго говоря, для вязкопластичных жидкостей Бингама-Шведова используется понятие обобщенного параметра Рейнольдса, который определяется через эффективную вязкость среды :

, (26)

и, в первом приближении, допускается определять по формуле (25), заменив в ней Re на . При погрешность не превышает 6%.