
- •1. Анализ вариации зависимой переменной в регрессии
- •2. Тест Дарбина – Уотсона некоррелированности случайных возмущений в схеме Гаусса – Маркова
- •3. Метод имитационного моделирования. Исследование последствий нарушения условий теоремы Гаусса – Маркова
- •4. Анализ вариации зависимой переменной в регрессии
- •5. Коэффициент детерминации как мера качества спецификации эконометрической модели
- •6. Компьютерное моделирование эконометрических систем
- •8. Процедура точечного прогнозирования по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной
- •9. Интервальное прогнозирование по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной
- •10. Множественная линейная регрессионная модель. Оценивание параметров множественной регрессии методом наименьших квадратов
- •11. Определение границ доверительных интервалов точечных оценок множественной регрессионной модели
- •12. Оценивание параметров модели взвешенным методом наименьших квадратов
- •13. Модель Марковица
- •14. Определение границ доверительного интервала прогноза зависимой переменной
- •15. Проверка гипотез относительно коэффициентов парной регрессии
- •16. Автокорреляция случайного возмущения
- •17. Гетероскедастичность случайного возмущения
- •18. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели множественной регрессии
- •19. Модель парной регрессии. Границы доверительных интервалов
- •20. Гетероскедастичность случайной компоненты. Тесты на наличие гетероскедастичности
- •21. Автокорреляция случайной составляющей. Тесты на наличие автокорреляции
- •22. Спецификация и преобразование к приведенной форме динамических моделей. Лаговые и предопределенные переменные динамической модели
- •23. Уточнение эконометрических моделей путем датирования переменных
- •24. Парная регрессия. Оценивание параметров методом наименьших квадратов
- •25. Тест Голдфелда–Квандта гомоскедастичности случайных возмущений в схеме Гаусса – Маркова
- •26. Дисперсионный анализ в парной регрессии
8. Процедура точечного прогнозирования по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной
Регрессионным анализом называется определение аналитического выражения связи между исследуемыми переменными, в котором изменение результативной переменной происходит под влиянием факторной переменной.
К
примеру модель парной регрессии ![]() (1)
(1)
создается как правило, для прогноза значений эндогенной переменной у по заданным значениям экзогенной переменной Х-регрессора модели.
Прогнозировать значения эндогенной переменной можно лишь тогда, когда модель признана адекватной. Модель называется адекватной, если прогнозы значений эндогенной переменной согласуются с ее наблюденными значениями. Таким образом, прогнозы по оцененной модели эндогенной переменной используются и в процедуре проверки адекватности данной модели.
Рассмотрим оптимальный точечный прогноз на примере.
Пусть модель (1)
оценена МНК по выборке ![]() (2) в ситуации, когда все предпосылки
теоремы Гауса-Маркова адекватны. Таким
образом, имеется оценка модели (1):
(2) в ситуации, когда все предпосылки
теоремы Гауса-Маркова адекватны. Таким
образом, имеется оценка модели (1):
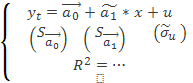 (3)
(3)
Пусть
![]() значение экзогенной переменной данной
модели;
значение экзогенной переменной данной
модели;
![]() прогноз.
прогноз.
Заметим,
что в рамках модели (1) пара ![]() связана с уравнением y0=a0+a1*x0+u0
(4), где случайный остаток u0
обладает, по предположению, количественными
характеристиками
связана с уравнением y0=a0+a1*x0+u0
(4), где случайный остаток u0
обладает, по предположению, количественными
характеристиками
m=E(u0)=0
Var(u0)=![]() (5)
(5)
Докажем
(см. задачу (3)), что в рамках модели (1) при
наличии информации об объекте-оригинале
в виде выборки (2) наилучший точечный
прогноз величины y0
вычисляется по правилу ![]() (6) т.е. в итоге подстановки в МНК-оценку
функции регрессии модели (1) значения
х=х0 экзогенной переменной. В свою
очередь, средняя квадратическая ошибка
прогноза (6) отыскивается по формуле:
(6) т.е. в итоге подстановки в МНК-оценку
функции регрессии модели (1) значения
х=х0 экзогенной переменной. В свою
очередь, средняя квадратическая ошибка
прогноза (6) отыскивается по формуле:
![]() (7)
(7)
где ![]() -1
-1
![]() (8)
(8)
![]() T
(9)
T
(9)
9. Интервальное прогнозирование по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной
Рассмотрим дробь
![]() ,
где
,
где ![]() -
прогнозное значение. Эта дробь имеет
смысл нормированно ошибки прогноза и
называется дробью Стъюдента. Заметим,
что эта величина является случайной
переменной (СП). При справедливости
сделанных предположений о случайном
возмущении модели дробь Стьюдента
обладает известным законом распределения
(ЗР) – распределением Стьюдента (или
t-распределением)
с числом степеней свободы
-
прогнозное значение. Эта дробь имеет
смысл нормированно ошибки прогноза и
называется дробью Стъюдента. Заметим,
что эта величина является случайной
переменной (СП). При справедливости
сделанных предположений о случайном
возмущении модели дробь Стьюдента
обладает известным законом распределения
(ЗР) – распределением Стьюдента (или
t-распределением)
с числом степеней свободы ![]() ,
где (k+1)
– количество оцениваемых коэффициентов
модели.
,
где (k+1)
– количество оцениваемых коэффициентов
модели.
Данное обстоятельство
позволяет построить замкнутый интервал
![]() с границами, именуемый доверительным,
который накрывает прогнозируемое
значение
с границами, именуемый доверительным,
который накрывает прогнозируемое
значение ![]() эндогенной переменной с принятой
доверительное вероятностью β. В последних
двух выражениях символом tкрит
обозначено критическое значение модуля
дроби Стьюдента.
эндогенной переменной с принятой
доверительное вероятностью β. В последних
двух выражениях символом tкрит
обозначено критическое значение модуля
дроби Стьюдента.
Обсужденная выше процедура интервального прогнозирования значений эндогенной переменной генерирует естественное правило объективной (формализованной) проверки адекватности оцененной модели:
-
Результаты наблюдений объекта-оригинала (выборку) разделить на два класса. В первый класс, именуемый обучающей выборкой, включить основной объем результатов наблюдения объекта-оригинала (90-95% выборки X,
 .
Оставшиеся результаты наблюдений
(например, пара (x0,y0))
составляют контролирующую
выборку.
.
Оставшиеся результаты наблюдений
(например, пара (x0,y0))
составляют контролирующую
выборку. -
По обучающей выборке оценить МНК-модель.
-
Задаться доверительной вероятностью β и по значениям регрессоров, входящих в контролирующую выборку (например, по значению x0), построить доверительные интервалы для соответствующих этим регрессорам значений эндогенной переменной модели (например, y0).
-
Проверить, попадают ли значения эндогенной переменной из контролирующей выборки (например, значение y0) в соответствующие доверительные интервалы (например, в интервал
 .
Если да, то признать оцененную модель
адекватной; если же нет, то оцененная
модель не может быть признана адекватной
и подлежит доработке.
.
Если да, то признать оцененную модель
адекватной; если же нет, то оцененная
модель не может быть признана адекватной
и подлежит доработке.
Процедуры интервального прогнозирования и проверки адекватности модели требуют значений tкрит. Чем выше значимость прогнозов, тем большее значение доверительное вероятности приходится принимать.
