10. Множественная линейная регрессионная модель. Оценивание параметров множественной регрессии методом наименьших квадратов

Множественная линейная регрессия позволяет построить и проверить модель линейной связи между одной зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x₁,...,x_р ), где у - зависимая переменная (результативный признак); х₁,...,х_р - независимые переменные (факторы).

Для построения уравнения множественной регрессии чаще используются следующие функции:

• Линейная – y=a+b₁x₁+b₂x₂+…+b_px_p+ε

• Степенная -

• Экспонента -

• Гипербола -

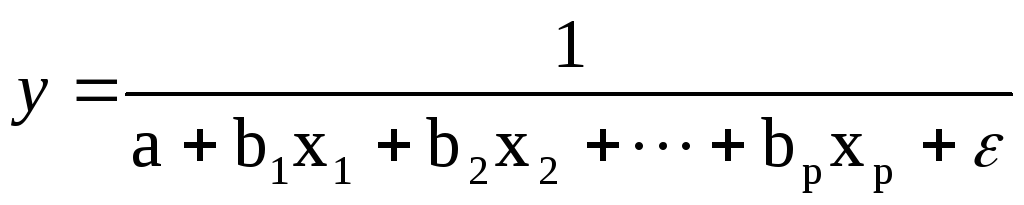
Можно использовать и другие функции, приводимые к линейному виду

Спецификация модели включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Требования к факторам.

1. Они должны быть количественно измеримы.

2.Факторы не должны быть коррелированы между собой и тем более находиться в точной функциональной зависимости.

Независимая переменная Y характеризует состояние или поведение экономического объекта. Набор переменных X₁,…,X_k, характеризуют этот экономический объект качественно или количественно. Предполагаем, что переменные X оказывают влияние на переменную Y, т. е. реализации переменной Y выступают в виде функции, значения которой определяются. правда, с некоторой погрешностью, значениями объясняющих переменных, выступающих в роли аргументов этой функции, т. е.

Y = f(X₁,…,X_k) + ,

где  - случайная компонента

МЛРМ –

Пример:

где Q^D  объем спроса на масло,

Х  доход,

P  цена на масло,

PM  цена на мягкое масло.

Здесь нам неизвестны коэффициенты  и параметры распределения .

Для их оценки имеется выборка из N наблюдений над переменными Y и X₁,…,X_k.

Для каждого наблюдения должно выполнятся следующее равенство:

Матричная форма записи МЛРМ

Г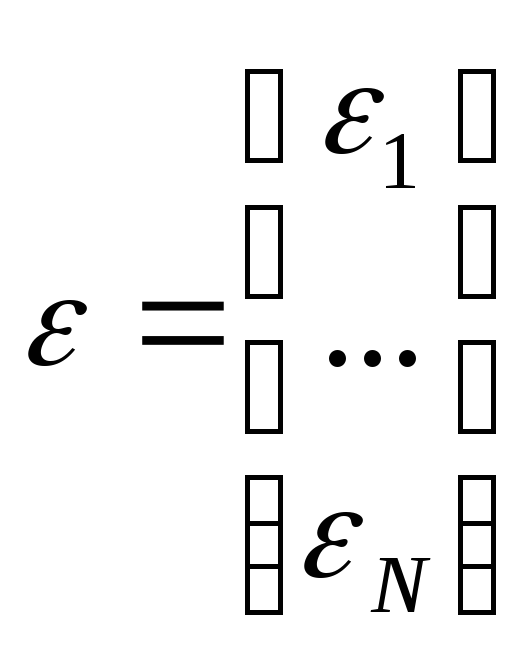де

Метод наименьших квадратов

Среди всех возможных гиперплоскостей выбираем ту, для которой сумма квадратов остатков минимальна

Будем минимизировать

Минимизация

или

Система нормальных уравнений

Вывод формулы для нахождения коэффициентов в матричном виде

Вывод формулы для нахождения коэффициентов в матричном виде

итог

- МНК оценки коэффициентов МЛРМ

11. Определение границ доверительных интервалов точечных оценок множественной регрессионной модели

Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x₁,...,x_р), где у - зависимая переменная (результативный признак); х₁,...,х_р - независимые переменные (факторы).

Определение границ доверительного интервала

1) Находим оценки параметров спецификации (коэффициенты регрессии а^0, а^1, а^2, оценки среднеквадратичного отклонения коэффициентов регрессии S_a0, S_a1, S_a2 и т.д.):

2) Далее, выбираем строку и обозначаем ее прогнозом. Настоящее значение функции обозначим Yp.

3) Следующим шагом необходимо рассчитать прогнозное значение Y^p, используя полученные оценки коэффициентов регрессии (см. рисунок).

В большинстве случаев налицо явное несовпадение результата и прогноза. Но ожидать точное совпадение прогноза и результата по меньшей мере наивно. Во-первых, Y^p - величина случайная, т.к. все три оценки коэффициентов a^0, a^1, a^2 вычислялись через значения случайной величины Y. Во-вторых, значение Yp содержит в себе неизвестное значение случайной составляющей ε_р. Все, что мы можем предпринять в этой ситуации, это проверить, попадают ли оба значения в доверительный интервал и делать заключение по этому факту.

Величина доверительного интервала зависит от дисперсии прогноза, которая складывается из дисперсии εt - случайной составляющей эконометрической модели и дисперсии случайной величины оценки регрессии (уравнение регрессии), значения коэффициентов которой вычислены с помощью функции ЛИНЕЙН (см. рисунок).

Однако оценки коэффициентов a^0, a^1, a^2 зависимы и для оценки их влияния на точность прогноза мало знать только их дисперсии, но нужно учесть и их взаимную зависимость, т.е. ковариацию, которая задается матрицей ковариаций.

Матрица ковариации регрессии оценивается по следующей формуле: Cov(A^) = S²_ε*(X^T*X)^-1, где A^ = ( a^0, a^1, a^2 )^T, оценки коэффициентов регрессии; S²_ε - дисперсия случайной составляющей ε.

4) Далее производим следующие вычисления:

1. (X^T*X)^-1.

2. , где .

5) Определим доверительный интервал для прогноза как (Y^p-tα*Sпрог, Y^p+tα*Sпрог), где tα-статистика Стьюдента, вычисляемая по формуле EXCEL СТЬЮДРАСПОБР.

Если оба значения (т.е. Yp и Y^p) попадают в указанный интервал, то модель признается адекватной и пригодной для целей прогнозирования.