12. Основная модель монтажного пространства.

Монтажным пространством элементов конструкций называется некоторая область, ограниченная габаритами этих элементов. Двумерное монтажное пространство называется монтажным полем. Различают регулярное и нерегулярное монтажное поле.

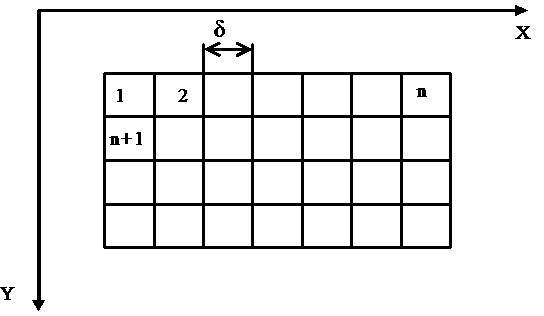
Минимальный размер ячейк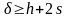и .Где h – ширина проводника, s – минимальное расстояние между проводниками.

Общее число дискретных ячеек:

.

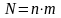Место любого i-го дискрета на монтажном поле однозначно может быть указано его координатами (x_i, y_i) в системе дискретных координат, либо индексом I

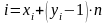
дискрет → код

Машинный эквивалент дискретного монтажного поля - двумерный массив B (X,Y), значения каждого элемента которого соответствуют состоянию дискрета с координатами X, Y,

либо одномерный массив B(I).

→ 0 Þ возрастает класс точности ПП

13 Основные классы задач математического программирования.

1. Класс линейного программирования

2. Класс нелинейного программирования

3. Класс целочисленного программирования

4. Класс динамического программирования

1. Класс линейного программирования - используется в случае, когда выходные параметры системы можно записать в виде линейных равенств и неравенств (хотя бы в приближении – кусочно-линейными аналогами)

Математическая формулировка:

определить такие значения переменных X*, удовлетворяющих системе ограничений, при которой достигается максимум (минимум) целевой функции F(X).

2. В задачах нелинейного программирования, в большинстве случаев, нелинейность связана с эмпирическими соотношениями, такими, как выход годной продукции, показатели качества изделий и т. п., а также с необходимостью учета случайных факторов, описываемых их функциями распределения.

Математическая формулировка:

определить такие значения переменных X* = {x*₁, x*₂, ..., х*_n}, удовлетворяющие системе n + m ограничений

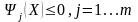
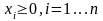
при которых достигается максимум (минимум) целевой функции F(X).

3. Все или часть переменных принимают только целочисленные значения.

В общем виде задача целочисленного программирования формулируется аналогично задачам нелинейного программирования: требуется найти план Х*, соответствующий минимуму (максимуму) целевой функции n переменных F(x) при ограничениях

x_i – целые числа.

4. Процесс поиска решения разбивается на отдельные этапы (шаги). На каждом шаге принимается одно из допустимого множества L решение, результатом которого является преобразование плана задачи. Управляющие операторы должны выбираться таким образом, чтобы максимизировать (минимизировать) F(N).

Преобразования, выполненные на последующих шагах, не должны оказывать никакого влияния на предыдущие шаги.

В основе теории динамического программирования лежит принцип оптимальности Р. Беллмана, согласно которому любой отрезок оптимальной траектории оптимален.

Любое правило поиска решения, которое дает допустимую последовательность решений, называют стратегией (политикой).

14.Прикладные задачи линейного программирования. Решение задачи о назначениях симплекс-методом.

Прикладные задачи :

Транспортная задача - (задача прикрепления поставщиков к потребителям) связана с нахождением наиболее рационального прикрепления пунктов отправления грузов к пунктам их назначения, при котором общая стоимость всех перевозок минимальна.

Задача о назначениях-частный случай транспортной задачи, который используется при проектировании ЭА.

Симплекс-метод(осуществляется направленное движение по опорным планам до получения оптимального решения).

Алгоритм:

1) По определенному правилу находим какую-либо вершину, принадлежащую множеству допустимых решений. Проверяем, не соответствует ли данная вершина оптимальному значению целевой функции. Если да, то задача решена.

2) Если задача не решена, то проверяем, нельзя ли на данном шаге утверждать, что целевая функция не ограничена сверху (снизу) на множестве допустимых решений при отыскании максимума (минимума) функции. Если да, то задача не имеет решения.

3) Если задача имеет решение, то находим новую вершину, в которой целевая функция имеет более оптимальное значение. Далее решение осуществляем в соответствии с пунктом 1, принимая в качестве исходной вновь выбранную вершину.

Для решения задачи линейного программирования этим методом необходимо, чтобы ее математическая модель была задана в канонической форме (y + Ax = B), т.е. все переменные должны быть положительными, а ограничения иметь вид равенств.

Если этого нет, то изменением начала координат всегда можно добиться положительности всех переменных, а за счет введения дополнительных неосновных переменных yi перейти от неравенств к равенствам.