3.5. Теоретико числовые преобразования (тчп)

ДПФ в поле комплексных чисел использует, как правило, приближенное представление числа и характеризуется погрешностью вычисления. В ряде задач обработки сигналов, связанных с вычисление сверток, необходимы точные преобразования инвариантные к циклическому сдвигу. Указанным требованиям удовлетворяют преобразования, осуществляющие модульную обработку в кольце целых чисел. Такие преобразования называются теоретико-числовыми (ТЧП).

Прямое и обратное ТЧП задаются формулами

mod M

mod M, (93)

где - целое число такое, что ; N^-1 – число, обратное N по модулю M.

ТЧП имеет ту же структуру, что и ДПФ. Иными словами, ТЧП – это дискретные преобразования Фурье, определенные в кольце чисел по модулю M. ТЧП обладают свойством цикличности свертки и в ряде случаев могут вычисляться с использованием только операций сложения и сдвига ( ). Свойства ТЧП и их применение в существенной степени зависят от параметров преобразования: модуля M, корня и длины N преобразуемой последовательности. Отсчеты входных данных для ТЧП обязательно должны быть промасштабированы, в частности должно выполняться условие .

Для того, чтобы выполнялось обратное ТЧП необходимо, чтобы существовали обратные числа N^-1 и . Это условие выполняется если и N взаимно простые с M. С точки зрения теории чисел обратные числа существуют если

и

или

, . (94)

Обычно определение ТЧП начинается с выбора модуля M, а затем исследуются возможные значения N. В качестве модуля чаще всего используют числа Мерсенна и Ферма. Соответственно различают ТЧП Мерсенна (ТЧПМ) и ТЧП ферма (ТЧПФ).

ТЧП – Мерсена

Числа Мерсенна определяются выражением , где - простое число. ТЧПМ существует, если N делит все числа вида (q_i - 1), где q_i- составные множители из разложения числа Мерсенна

.

Для простых чисел Мерсенна длину преобразуемой последовательности получают из условия, что число N делит число т.е.

Из теории чисел известно, что если , то делится на , и Кроме того число 2 является делителем числа . Следовательно, можно определить -точечные ТЧПМ.

Рассмотрим вопрос определения . Если простое, то корнем порядка является 2 так как . Если составное число то, 2 тоже является корнем, но необходимо чтобы имело обратное число, а это условие выполняется в том случае если

.

Таким образом, можно определить прямое и обратное точечное преобразование Мерсена.

и

, (95)

где .

Для 2p точечного преобразования корнем является так как и степени корня представляют собой разные числа отличные от нуля.

Для составного M_p необходимо выполнить проверку на взаимную простоту чисел:

для .

Для то получаем:

.

Следовательно, можно определить 2p-точечное ТЧПМ

,

, (96)

где .

Для преобразования осуществляются без операций умножения. Возможно ТЧПМ другого размера с , но в этом случае появляются операция умножения.

Пример. Пусть ,

,

Матрица ТЧП строится так же как матрица преобразований Фурье с одним отличием: место поворачивающего множителя занимает число

Определим

,

используя алгоритм Евклида:

, .

Обратное ТЧПМ имеет вид

.

Недостаток преобразования Мерсенна состоит в том , что для него отсутствуют алгоритмы быстрого вычисления, так как числа p и 2p не разлагаются на большое количество сомножителей. Этого недостатка лишены преобразования Ферма (ТЧПФ).

ТЧП Ферма

ТЧПФ в качестве корня использует двойки и степени двойки. Это позволяет получить удобную арифметику, N кратную степени двойки.

Числа Ферма имеют вид , где . Например .Первые пять чисел – это простые числа остальные числа составные. , где - простое число. Если - простое число, то размер выборки определяется из условия: .

Если - составное число, то простой множитель имеет вид.

Следовательно всегда можно найти такое -точечное преобразование по модулю, для которого выполняется условие:

Определим корни преобразования. Если то он является конем порядка . Действительно, по модулю , а величины принимают различных значений.

ТЧПФ имеет вид

mod

, (97)

где .

Возможны следующие виды «удобных» корней:

• корень , является корнем порядка по ;

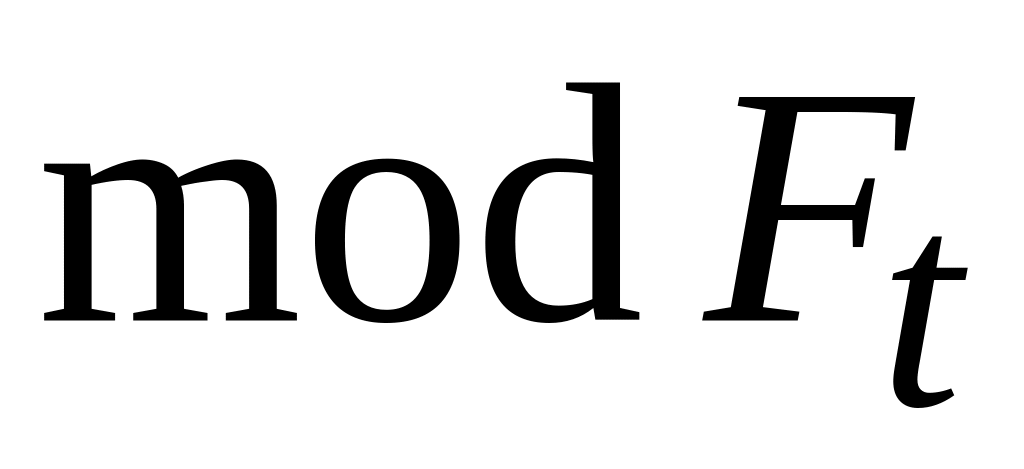• корень 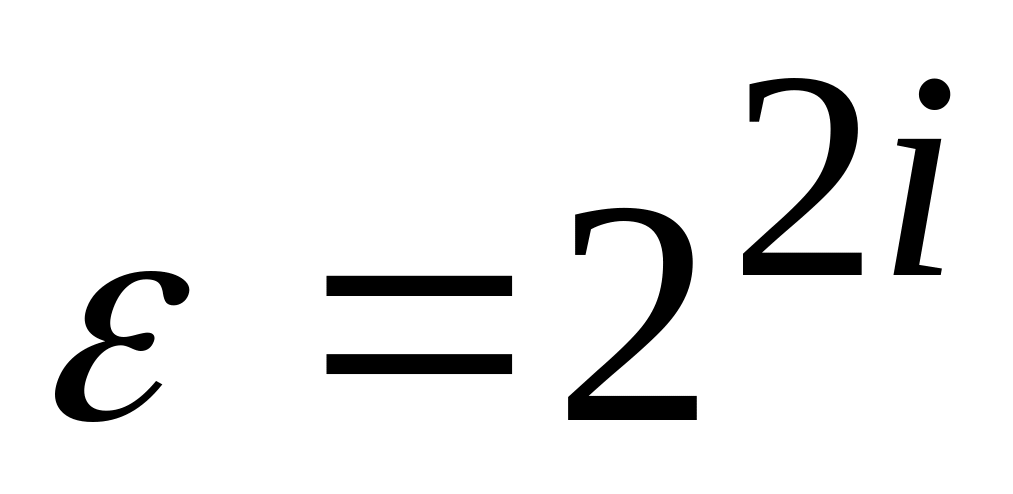является корнем порядка: 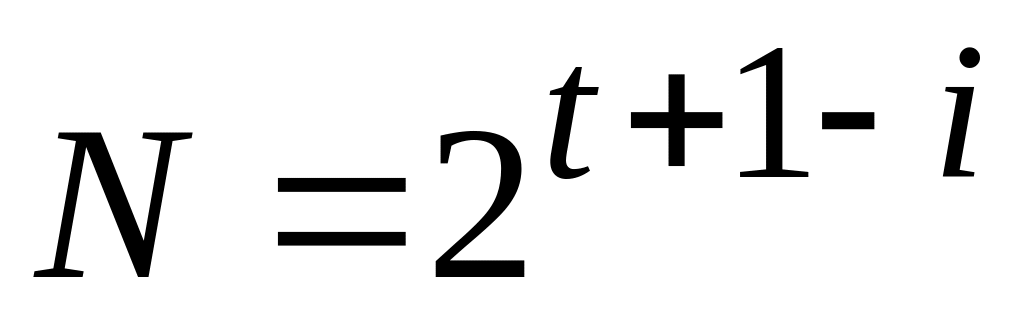по ;

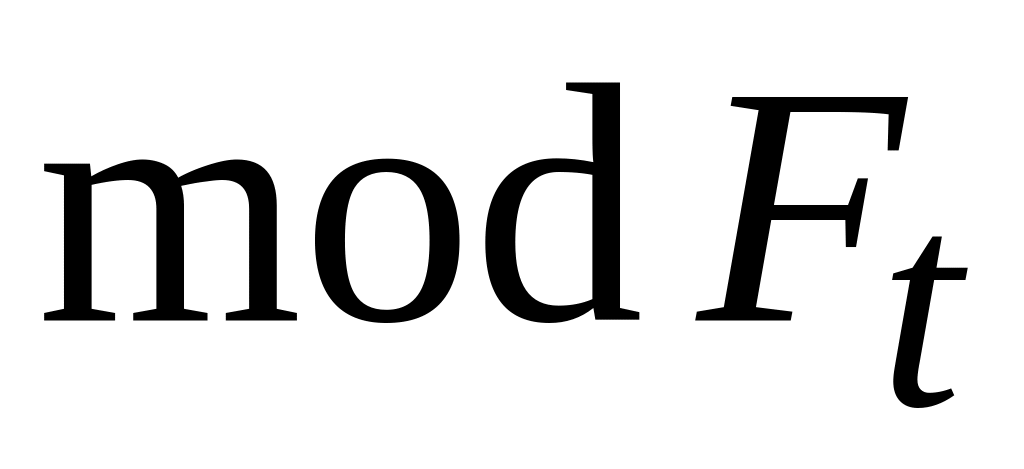• корень , , .

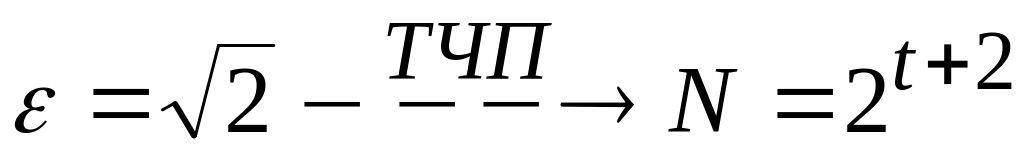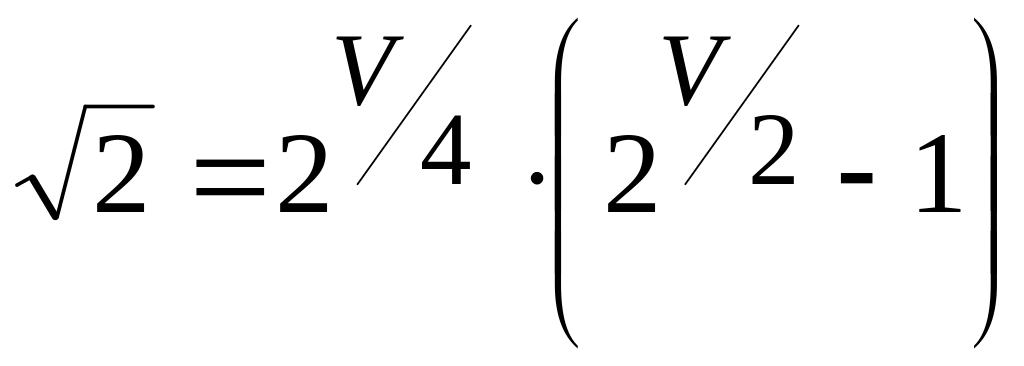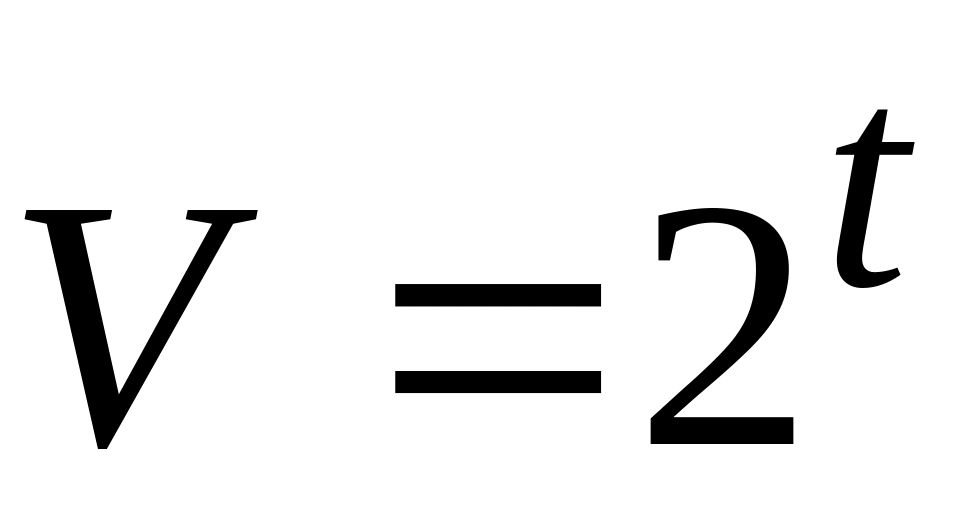ТЧПФ имеет длины преобразований, которые выражаются составными числами. Это позволяет для их вычисления воспользоваться алгоритмами типа БПФ. - Так, если длина равна степени двойки, то возможны быстрые алгоритмы преобразований, структура которых аналогично БПФ с прореживанием по частоте и по времени за исключением того, что операционный умножитель на поворачивающий множитель заменяется операцией умножения на степень двойки, то есть сдвигами:

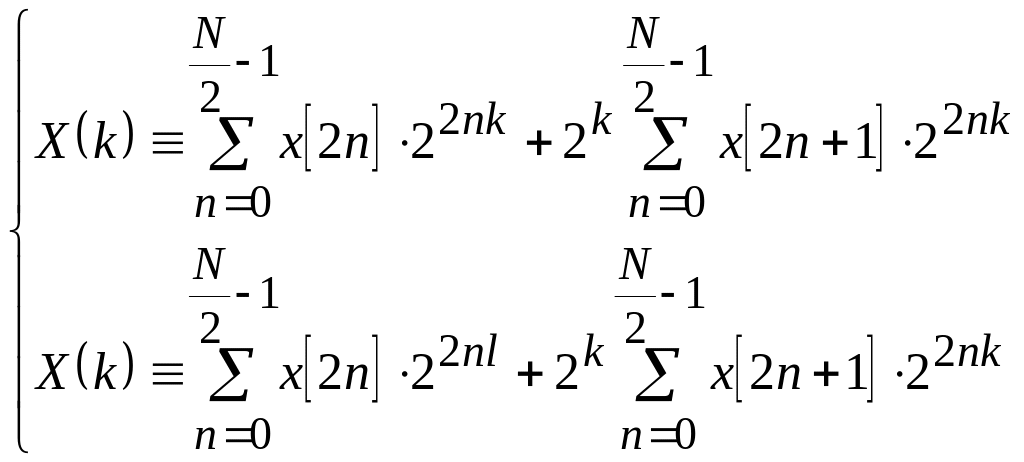. (98)

Вычислительная сложность быстрого ТЧПФ составит - операций сложения и - операций сдвига.

Пример. Пусть ; . Тогда для . Для .

Выберем тогда:

.

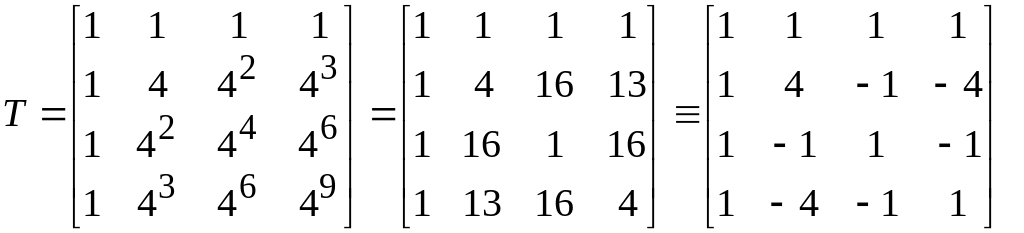
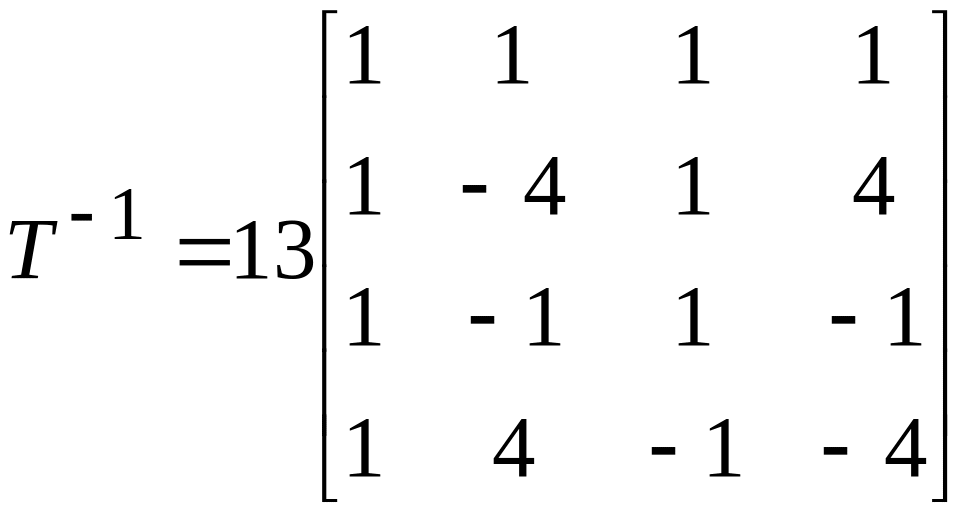Основные применения ТЧП - это вычисление точных значений свертки.

Пример. Предположим, необходимо вычислить циклическую свертку двух последователь­ностей и . Выберем ТЧПФ с параметрами . Спектры последовательностей равны:

и .

Произведение одноименных спектральных коэффициентов дает следующий результат . Обратное число . Значения циклической свертки равны:

.