Дискретное преобразование Карунена – Лоэва Оптимальное преобразование

Пусть x = [x[1], x[2], …, x[M]]^T – случайный вектор с нулевым средним и корреляционной матрицей R_x. Подвергнем этот вектор линейному преобразованию

w = A^Hx ; A ^–1 = A^H, (1)

где A = [ a_j ], j = 1,…, M – унитарнаяя матрица. При этом

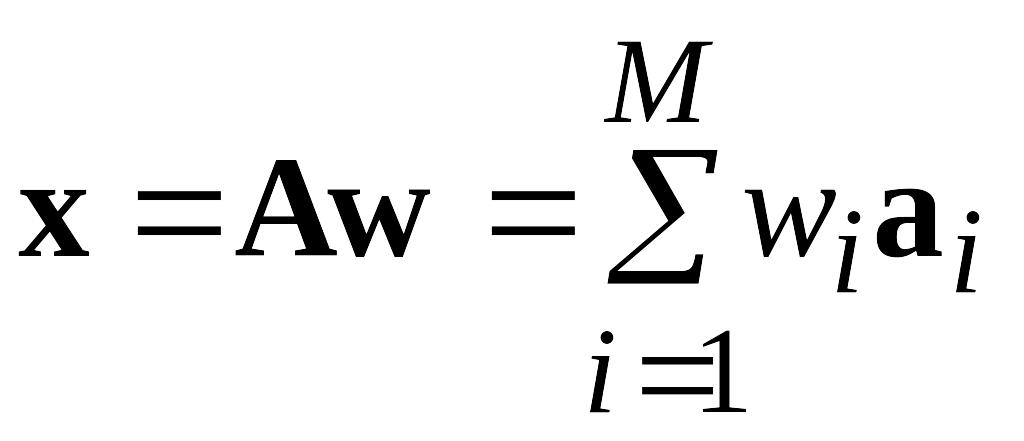; при i  j.

Рассмотрим оценку вектора x в форме m компонент (1  m  M ) вектора w

.

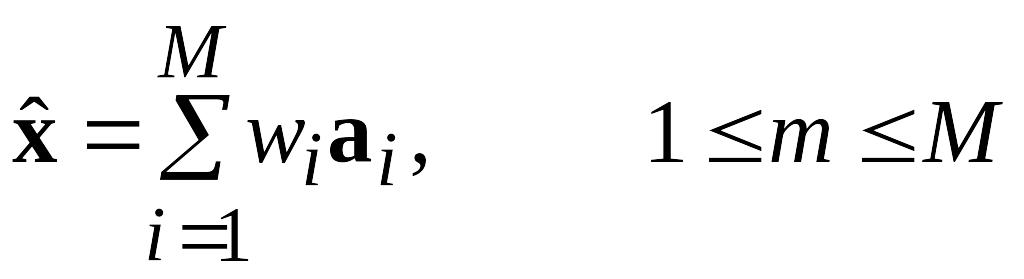Ошибка принимает вид

,

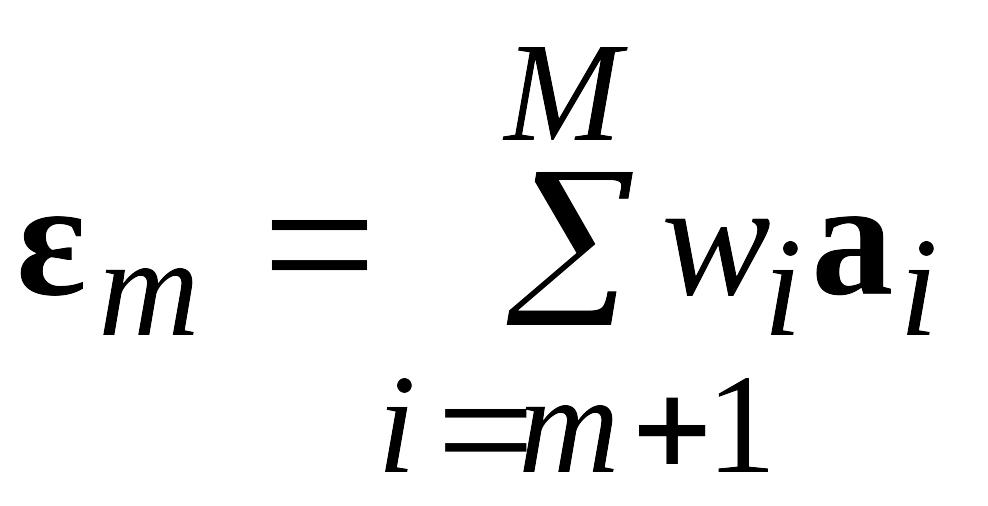при этом средний квадрат ошибки

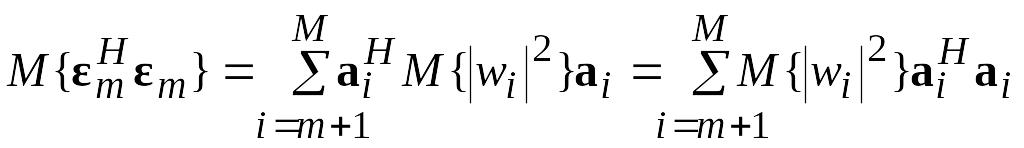. (2)

Из (1) следует, что и следовательно .

Определим такую матрицу A, которая минимизировала бы средний квадрат ошибки, при условии нормировки вектора a_i:

.

Задача сводится к поиску минимума функции Лагранжа

,

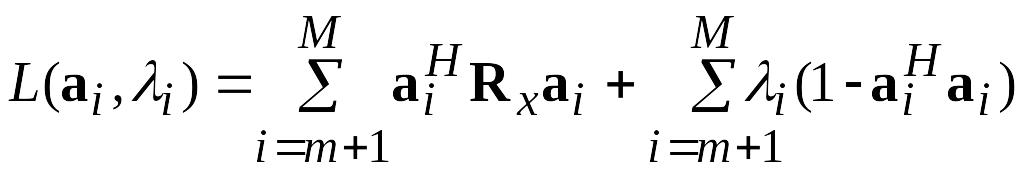где _I – множитель Лагранжа.

Приравнивая градиент этого выражения нулю, получим уравнение

,

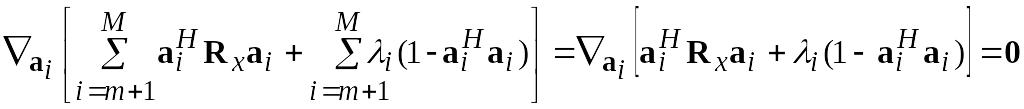из которого получается соотношение

R_xa_i = _ia_i. (3)

Используя данное соотношение и учитывая (2) выразим минимальную ошибку как

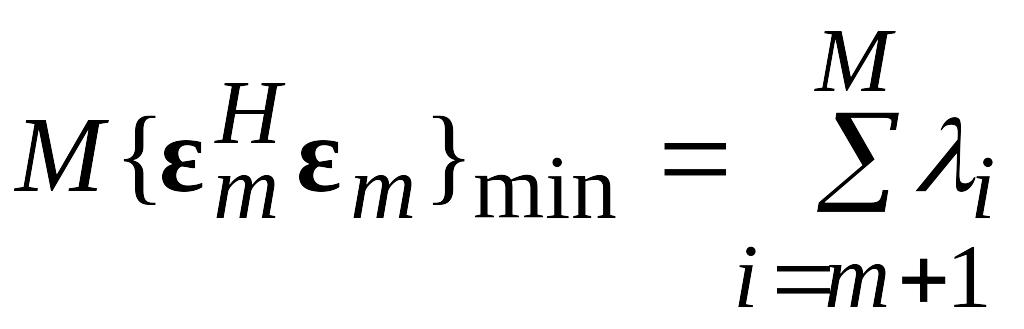. (4)

Из (3), (4) и определения собственных значений и векторов следует, что задача минимума среднего квадрата ошибки сведена к поиску собственных значений _i и собственных векторов a_i матрицы R_x. Следовательно, матрица преобразований A является матрицей состоящей из ортонормированных собственных векторов матрицы R_x . Обозначим эту матрицу через Q = {q_i}, i=1,…, M.

Тогда

W = Q^H x. (5)

В результате преобразования (5) формируется вектор w с нулевым средним значением и с корреляционной матрицей

 = diag(₁, …, _M).

Такое преобразование называется дискретным преобразованием Карунена-Лоэва (ДПКЛ).

Обратное преобразование выражает вектор x через координаты вектора w:

x = Q w = q₁ w₁ + q₂ w₂ , + … + q_M w_M.

Дискретное разложение Карунена – Лоэва периодической случайной последовательности.

Известно, что корреляционная матрица стационарного процесса является теплицевой. Если корреляционная последовательность случайного процесса является периодической с периодом M , то корреляционная матрица становится циркулянтной. Общий вид циркулянтной матрицы

.

Любая строка такой матрицы получается из предыдущей путем циклического сдвига га одну позицию вправо.

Циркулянтная корреляционная матрица имеет вид

.

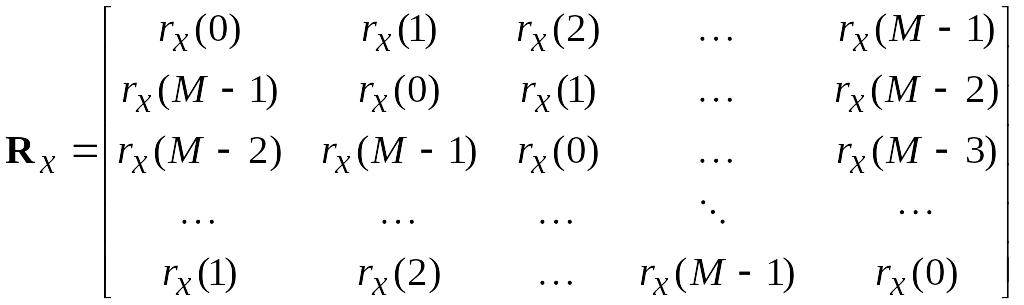Введем M – точечное ДПФ последовательности отсчетов корреляционной функции r_x(l)

,

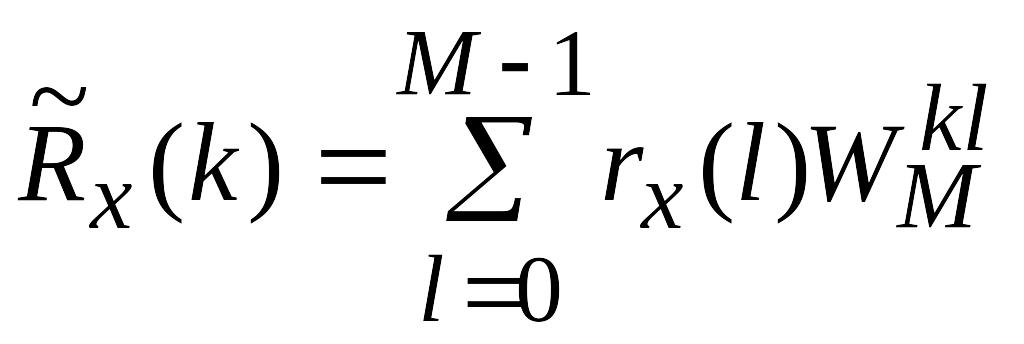где W_M = exp(-2j/M) .

Рассмотрим вектор

.

Нетрудно установить, что справедливо следующее соотношение

.

Отсюда следует, что вектор w_k ДПФ является собственным вектором циркулянтной корреляционной матрицы R_x, а величина - собственным значением этой матрицы. Таким образом, ДПФ эквивалентно ДПКЛ периодической импульсной последовательности.

Справедливо еще одно полезное соотношение

,

где w – матрица ДЭФ, которое говорит о том, что ДПФ диагонализирует циркулянтную корреляционную матрицу.

Пример. Дано разностное уравнение

x[n] = v[n]+bv[n-1],

где v[n] – белый гауссовский шум с нулевым средним значением и единичной дисперсией.

Найти ДПКЛ при M = 3.

Решение. Найдем матрицу R_x

.

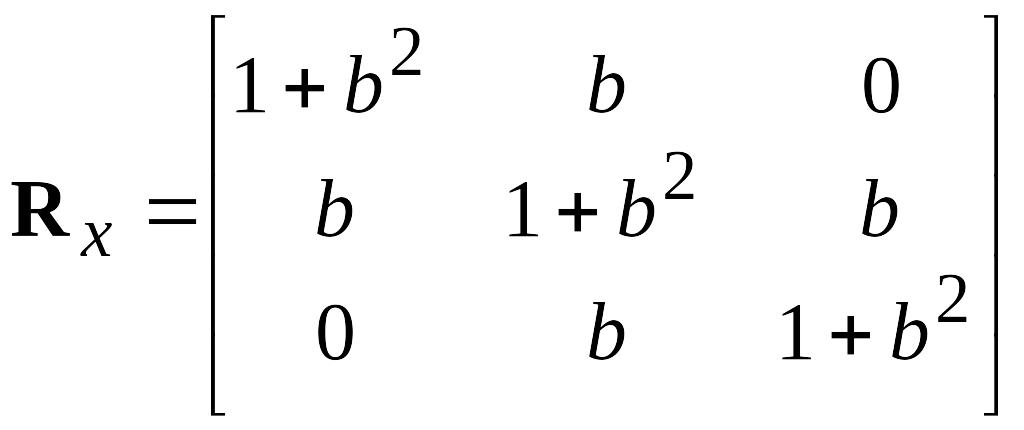Вычислим собственные значения матрицы R_x:

| R_x - I|=(1 + b² - )[(1 + b² - )² –2b²] = 0.

Отсюда находим собственные значения

⁽¹⁾ = 1 + b²; ^(2,3) = 1 + b²  b2.

Матрица Q состоит из ортонормированных собственных векторов

Q = [q₁, q₂, q₃]

матрицы R_x:

.

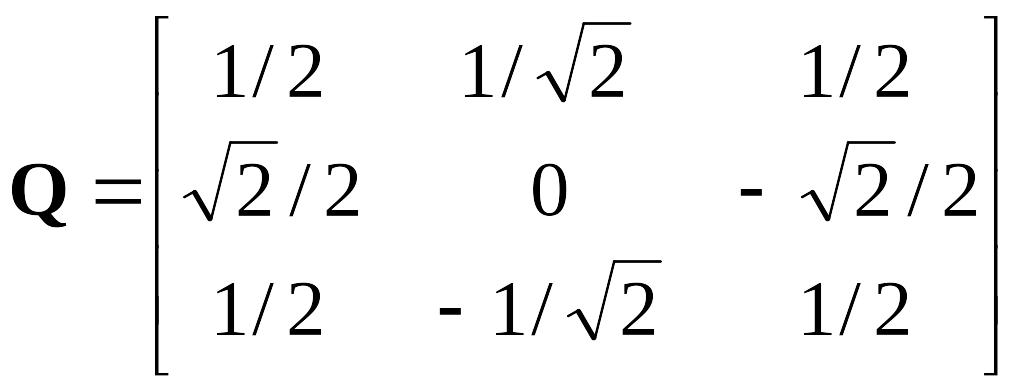ДПКЛ принимает вид

x(n) = w₁(n) q₁ +w₂(n) q₂ +w₃ q₃.

Причем M{w₁²} = ₁, M{w₂²} = ₂, M{w₃²} = ₃ .