3.2.1. Бпф по смешанному основанию

ДПФ последовательности , N = N₁ N₂ запишется в виде

.

Представим входные n и выходные k индексы в смешанной системе счисления с основаниями N₁ N₂:

; , где , .

Последовательности входных и выходных отсчетов преобразуются в двумерные массивы:

, , ;

, , .

После подстановки алгоритм ДПФ представляется в виде

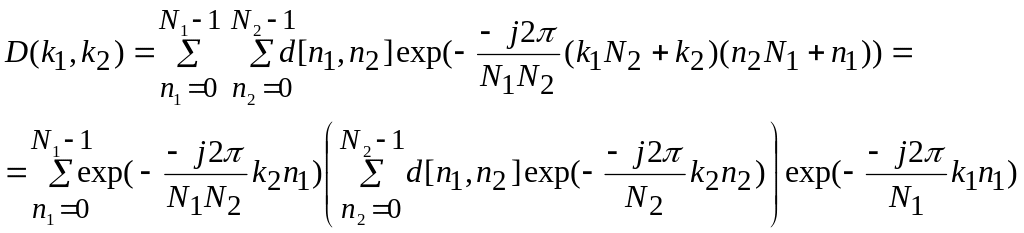(53)

Таким образом, исходное ДПФ оказалось сведенным к двум ДПФ, производимым над уменьшенными массивами. Алгоритм преобразования может быть представлен следующей трехэтапной схемой.

1. Для всех строк матрицы вычисляются N₂ точечные ДПФ.

2. Каждый элемент полученной матрицы умножается на фазовый множитель .

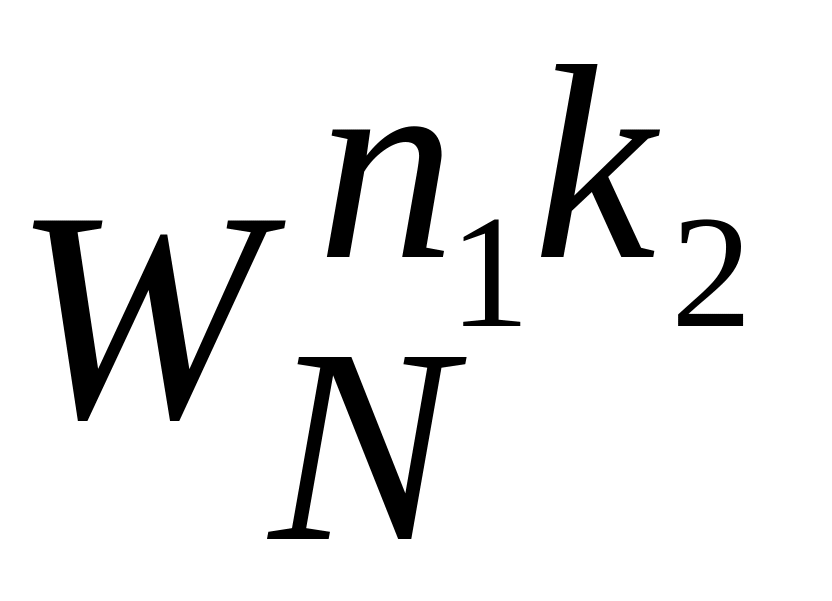3. Для всех столбцов матрицы, полученной на втором этапе, вычисляются N₁ точечные ДПФ.

Заметим, что алгоритм имеет инверсный порядок следования индексов в выходной последовательности. Это объясняется инверсией разрядов в позиционно-численном представлении индексов по смешанному основанию. Для сохранения естественного порядка следования отсчетов необходимо выполнить операцию обратной перестановки.

Вычислительные затраты при таком способе вычисления ДПФ равны: количество операций умножения равно ; сложений .

Если числа N₁ и N₂ являются составными, то алгоритм БПФ применяется рекурсивно. При этом на каждом шаге рекурсии БПФ сокращает число операций.

Пример. Пусть N = 6 = 23, N₁ = 2, N₂ = 3. Входная последовательность имеет вид

{x[n]; n = 0,..,5} = [1,1,1,-1,-1,-1]. Требуется вычислить ДПФ по смешанному основанию.

Элемент матрицы двумерного массива в этом случае равен

d[n₁,n₂] = x[2n₂ +n₁], n₁=0,1; n₂ = 0,1,2.

Сама матрица имеет вид

.

На первом этапе алгоритма вычислений, строки матрицы входных отсчетов преобразуются с помощью трехточечного ДПФ. В результате получаем матрицу

.

После умножения элементов этой матрицы на поворачивающие множители , k₂ = 0,1,2, получаем матрицу

.

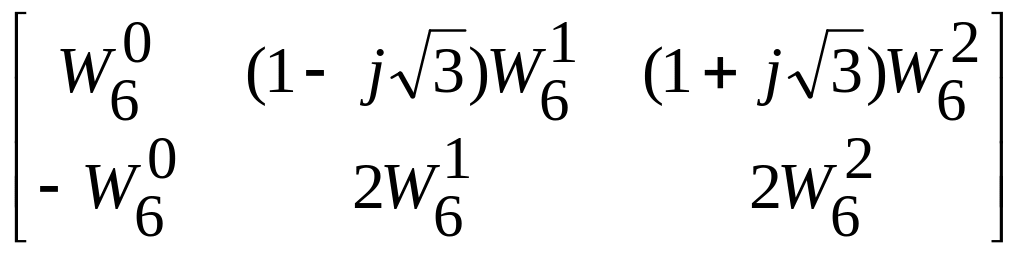Применение двухточечного ДПФ к столбцам матрицы, полученной на втором этапе, приводит к следующему результату

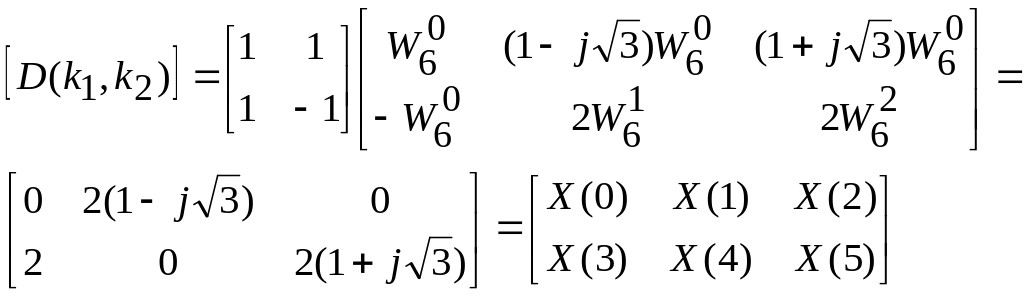
Спектр ДПФ равен

.

Описанный алгоритм предпочтительнее непосредственного прямого вычисления ДПФ, поскольку при этом требуется меньше арифметических операций. Действительно, сложность алгоритма ДПФ по смешанному основанию определяется сложностью вычислений N₁ ДПФ размера N₂ , N₂ ДПФ размера N₁ и N₁ N₂ умножений на фазовые множители. Вычислительные затраты при таком способе вычисления ДПФ равны: количество операций умножения равно ; сложений . Прямое вычисление ДПФ потребовало бы N² операций комплексного умножения и N(N-1 ) операций комплексного сложения.

Если числа N₁ и N₂ являются составными, то алгоритм БПФ применяется рекурсивно. При этом на каждом шаге рекурсии БПФ сокращает число операций.

3.2.2. Алгоритм Гуд-Томаса

Рассмотрим случай, когда необходимо вычислить N-точечное ДПФ, причем N=N₁N₂ и числа N₁ и N₂ являются взаимно простыми, т.е. НОД(N₁N₂)=1. В этом случае применим алгоритм Гуд-Томаса (ГТ) с использованием простых делителей. Используется отображение обрабатываемой последовательности в двумерную таблицу, позволяющая использовать двумерное преобразование Фурье.

Отобразим последовательности входных x[n] и выходных X(k) отсчетов в двумерные массивы

по следующим правилам:

- для индексов входного сигнала

; (54)

-для индексов выходного сигнала

. (55)

Обоснованность применения такого отображения доказывается следующим образом. Согласно китайской теоремы об остатках [ 1 ] существуют такие целые m₁ и m₂, что выполняется равенство , где . С другой стороны, для индексов выходного сигнала справедливо равенство

,

где Q₁ целая часть, дополняющая k₁ до k; Q₂-целая часть, дополняющая k₂ до k.

ДПФ двумерного массива данных запишется как

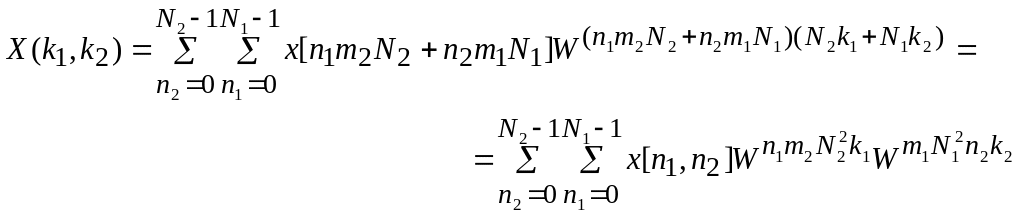(56)

С учетом того, что и получаем

и

.

Теперь видно, что ДПФ двумерного массива входных данных можно вычислить с помощью двумерного ДПФ

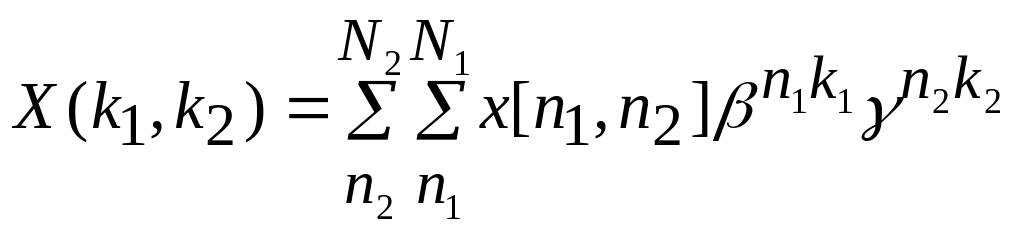. (57)

Элементы  и  являются простыми корнями из единицы степеней N₁ и N₂ , задающие соответственно N₁ –точечное и N₂-точечное преобразования Фурье.

Вычислительная сложность алгоритма оценивается как N(N₁ + N₂) операций умножений и сложений.

Пример. Необходимо вычислить ДПФ последовательности {x[n]; n=0,…,5} = (1,1,1,-1,-1,-1) с использованием алгоритма ГТ.

Длину обрабатываемых отсчетов N можно разложить на два взаимно простых множителя множителя

N = 23 = N₁N₂, N₁ = 2, N₂ = 3; НОД (N₁,N₂) = 1.

Алгоритм ГТ запишется как

,

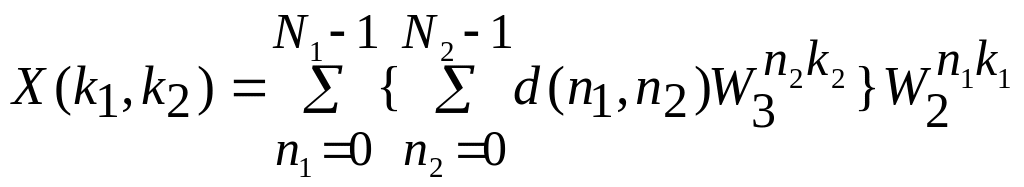n₁ = 0,…,N₁ , n₂ = 0,…,N₂ ; k₁ = 0,…,N₁ , k₂ = 0,…,N₂

Перестановка входных данных имеет вид:

n = n₁ m₂ N₂ + n₂ m₁ N₁ = n₁ m₂ 3 + n₂ m₁ 2,

где коэффициенты m₁ и m₂ определяются из решения диофантового уравнения

m₂ N₂ + m₁N₁ = 1  m₂ 3 + m₁2 = 1

Для решения диофантового уравнения применим алгоритм Евклида

3 = 21 + 1 или 1 = (1)3 + (-1)2,

откуда получаем, что m₁= -1 и m₂ = 1.

Матрица данных после перестановки имеет вид

Матрица внутреннего ДПФ равна

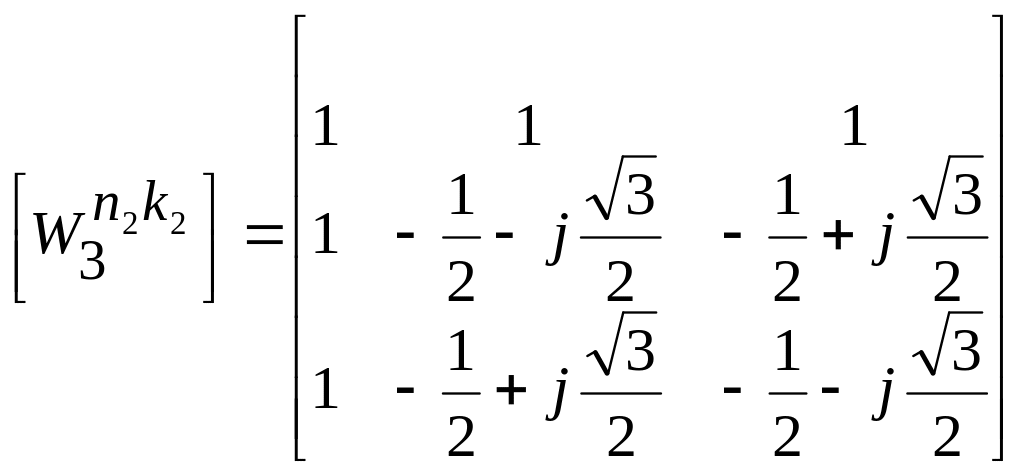, k₂ = 0,…,N₂, n₂ = 0,…,N₂.

Вычисление внутреннего ДПФ приводит к результату

Матрица внешнего ДПФ равна

, k₁ = 0,…,N₁, n₁ = 0,…,N₁.

В результате вычисления внешнего ДПФ получаем

Связь выходных отсчетов преобразования ГТ {X(k₁,k₂)} и отсчетов прямого ДПФ {X(k)} определяется исходя из соотношения

k = k₁ N₂ + k₂ N₁ mod N

и имеет вид

.

Откуда получаем значения спектральных коэффициентов прямого ДПФ

.