1.Матрицы: определение, действия над матрицами, вычисление примеры. Матрица-прямоуг табл-ца, сост-ая из чисел либо из других объектов. Определитель вычислить можно а матницу нельзя.Объкты из кот сост-а матр-а назыв элемент-ми матрицы. элем-ты матр располаг по строкам, столбцам, диагон-ям. Если число строк=числу столб-ов, мытриц назыв квадрант, иначе прямоуг.(нарисовать). Матрица характериз-ся размер-тью , если m-число строк, а n-число столб-ов, то размерность матрицы m×n. Действия над матрицами. Сложение матриц. Матрицы одинак размерности можно складывать: A=(a₁₁a₁₂a₂₁a₂₂), B=(b₁₁b₁₂b₂₁b₂₂), A+B=( a₁₁₊b₁₁ a₁₂₊b₁₂ a₂₁₊b₂₁ a₂₂₊b₂₂), умножение матрицы на число. Каждый элем-т матр умножается на это число. Св-ва действий. A+B=B+A, A+(B+C)=(A+B)+C, (j+ i)A=jA+iA, (IJ)A=(jA)i=(iA)j. перемножение матриц. Премножаются матрицы, у которых число столбцов 1 матр=числу строк 2 матр. A=(a₁₁a₁₂a₁₃ a₂₁a₂₂a₂₃), B=( b₁₁b₁₂b₁₂), A×B=( a₁₁b₁₁₊ a₁₂b₂₁₊ a₁₃b₃₁ a₂₁b₁₁₊ a₂₂b₂₁₊a₂₃b₃₁). Св-ва перемнож матр. A(B+C)=AB+AC, (B+C)A=BA+CA, A(BC)=(AB)C. Транспонир матриц. Операция над матр, при котор ее строки станов столбцами (с теми же номерами), а столбцы строками наз транспонир матр. A=(a₁₁a₁₂a₂₁a₂₂) A*=(a₁₁a₂₁ a₁₂a₂₂). Св-ва: (A+B)*=A*+B*, (kA)*+kA*, (AB)*+A*B*

2

3

Определители третьего порядка.

Рассмотрим квадратную матрицу (таблицу) третьего порядка

(1)

.

Если в этой матрице вычеркнуть любую строку и любой столбец, то оставшиеся элементы образуют квадратную матрицу второго порядка. Из квадратной матрицы третьего порядка можно получить девять квадратных матриц второго порядка. Введём несколько новых понятий.

Определение 1. Минором элемента матрицы третьего порядка называют определитель матрицы второго порядка, которая получается из данной матрицы вычёркиванием -ой строки и -го столбца, т.е. строки и столбца, на пересечении которых стоит данный элемент.

Минор элемента обозначается символом . Например, минором элемента матрицы (1) является определитель

(2)

.

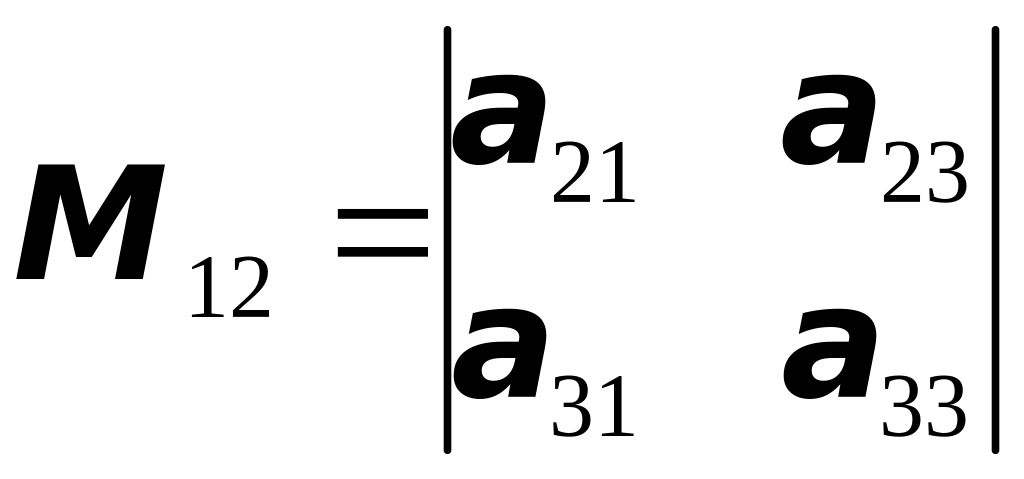
Определение 2. Алгебраическим дополнением элемента матрицы третьего порядка называют число, равное произведению минора этого элемента на .

Иначе: алгебраическое дополнение элемента - это минор, если сумма индексов чётная, и минор, взятый с противоположным знаком, если сумма индексов нечётная. Алгебраическое дополнение элемента обозначается , т.е. по определению .

Пример 1. Вычислить алгебраические дополнения и матрицы

.

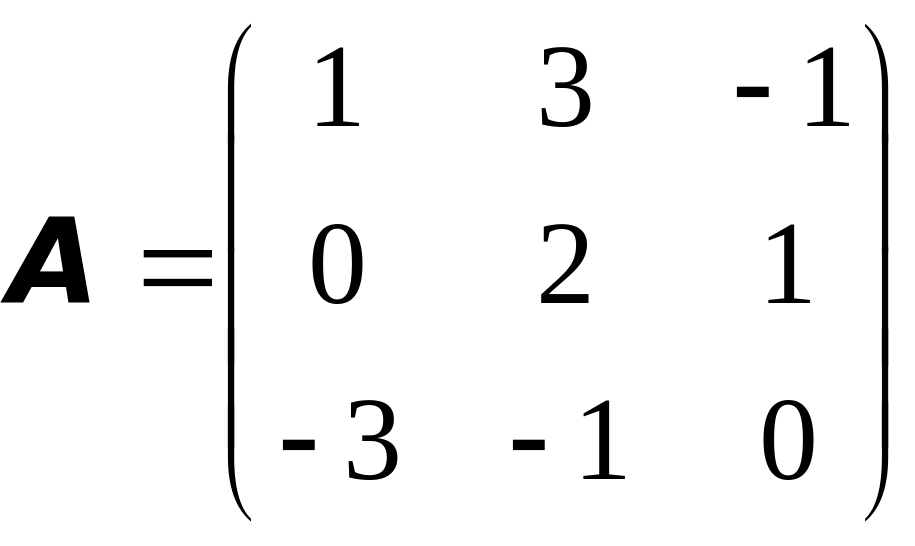Имеем

; .

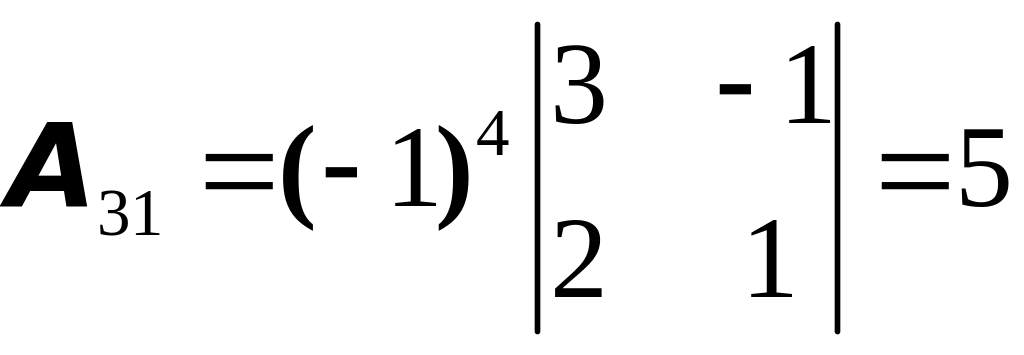Замечание. Можно говорить также о минорах и алгебраических дополнениях элементов матрицы второго порядка, если под определителем матрицы, состоящей из одного элемента (матрицы первого порядка), понимать число, равное этому элементу.

Определение 3. Определителем (детерминантом) квадратной матрицы третьего порядка (определителем третьего порядка) называем число, равное сумме попарных произведений элементов первой строки на их алгебраические дополнения. Т.е. по определению имеем

(3)

.

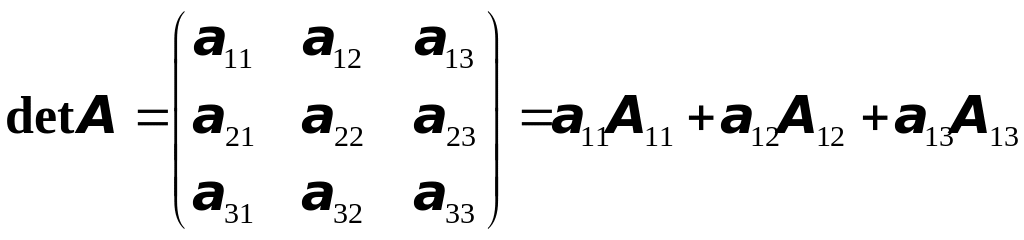
Пример 2. Вычислить определитель матрицы

.

Имеем

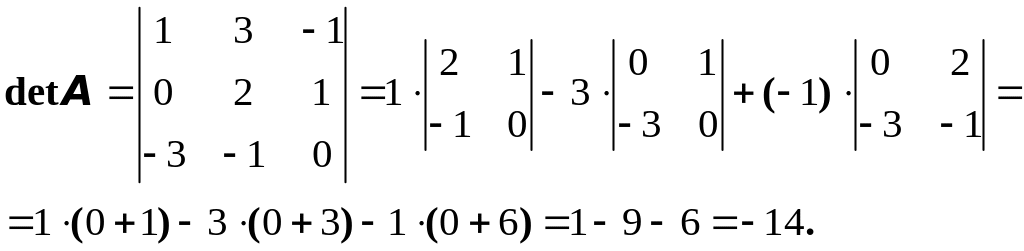
Замечание. Если в формулу (3) подставить выражения алгебраических дополнений через элементы матрицы, то получим

(4)

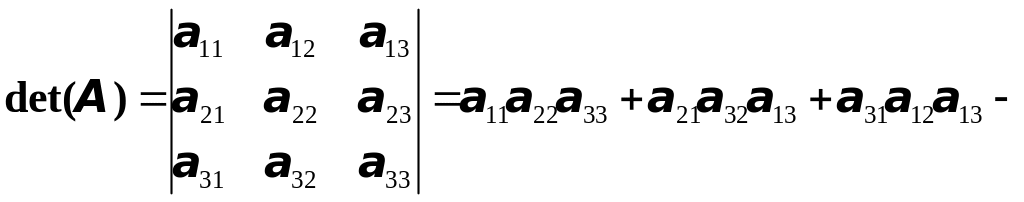
В этой формуле шесть слагаемых, причём каждое из них является произведением трёх элементов матрицы: по одному из каждой строки и из каждого столбца; три слагаемых входит со знаком «+», а три со знаком «-». В курсах высшей алгебры формула (4) принимается в качестве определения определителя третьего порядка.

§ 3. Основные свойства определителей 3-го порядка.

Нетрудно убедиться, что все свойства определителей 2-го порядка справедливы и для определителей 3-го порядка. Но как более сложный объект, определители 3-го порядка имеют и дополнительные свойства. Сформулируем и докажем все свойства полностью.

1.Определитель не изменяется, если его строки поменять местами с соответствующими столбцами, т.е.

(1)

.

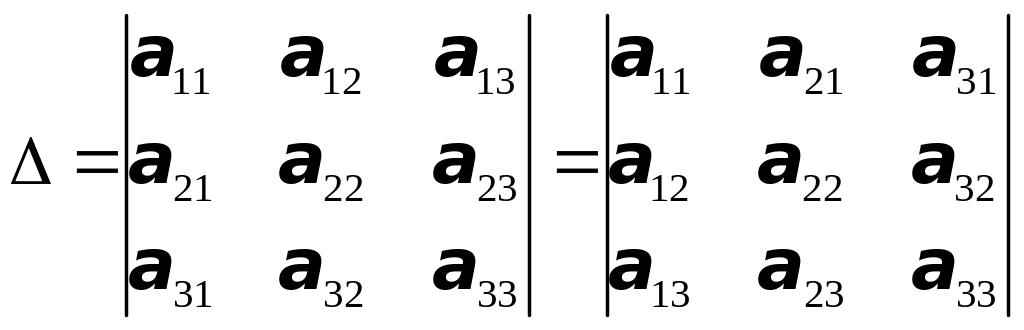
Доказывается разложением каждого определителя по элементам первой строки. В результате получаем одно и то же выражение.

2.Определитель равен сумме попарных произведений элентов любой строки (столбца) на их алгебраические дополнения.

Д

(2)

окажем, например, равенство

Имеем

.

Но

Следовательно, .

Это свойство называют свойством разложения по элементам строки или столбца.

3.При перестановке двух строк определитель меняет знак на противоположный.

Доказательство. Пусть в матрице третьего порядка перестановлены первая и третья строки. Покажем, что

(3)

Разлагая определитель, стоящий в левой части равенства (3), по элементам первой строки, получим

Разлагая же определитель, стоящий в правой части этого равенства, по элементам третьей строки, получим

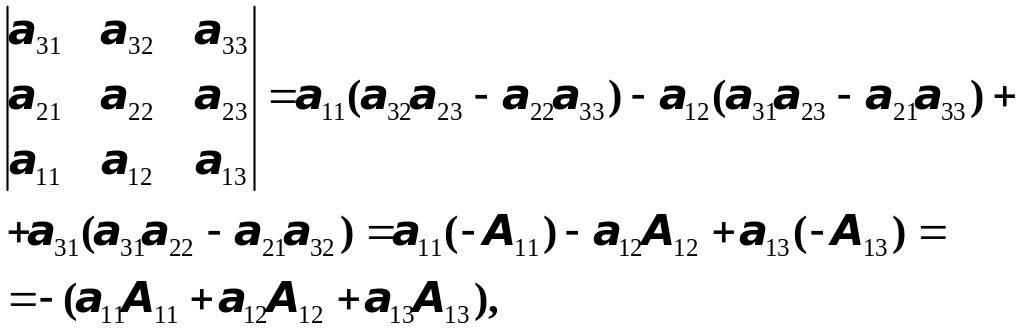
т.е. то же выражение, но с противоположным знаком.

4.Определитель с двумя одинаковыми строками (столбцами), равен нулю.

Доказательство. Пусть - определитель матрицы с двумя одинаковыми строками. Если эти строки переставить местами, то определитель должен поменять знак. Но так как строки одинаковы, то определитель не изменится. Т.е. имеем , откуда или

5.Если все элементы какой-либо строки определителя умножить на число К, то весь определитель умножится на это число.

Доказательство. Покажем, например, что

.

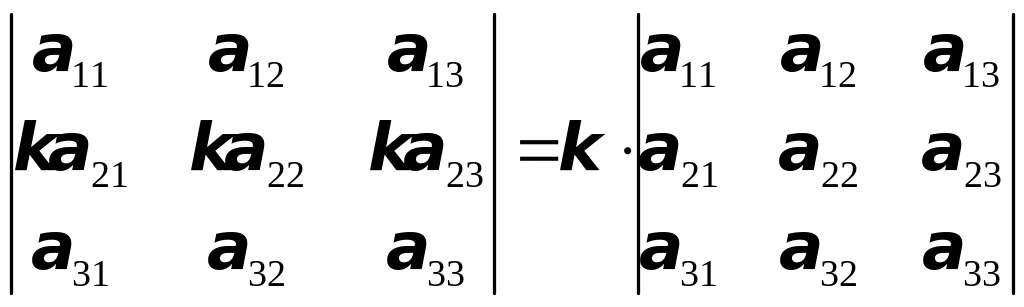Разложим по элементам второй строки. Тогда левая часть равенства может быть записана так:

где - определитель матрицы .

Это свойство иногда формулируют так: общий множитель всех элементов строки можно выносить за знак определителя.

6.Определитель, у которого соответствующие элементы двух строк пропорциональны, равен нулю.

Доказательство. Пусть, например, элементы третьей строки пропорциональны элементам первой, т.е.

Тогда, используя свойство 5, а затем 4, будем иметь

7.Определитель, у которого все элементы какой-либо строки пред-ставляют собой сумму двух слагаемых, равен сумме двух определителей, получаемых из данного заменой элементов рассматриваемой строки соответственно на первые и вторые слагаемые.

Доказательство. Пусть, например,

Тогда

8.Определитель не меняется, если к элементам какой-либо строки прибавить соответствующие элементы любой другой строки, умноженные на общий множитель

Доказательство. Прибавим, например, к элементам первой строки соответствующие элементы третьей строки, умноженные на одно и то же число . Тогда, по свойству 7, а затем по свойству 6, будем иметь

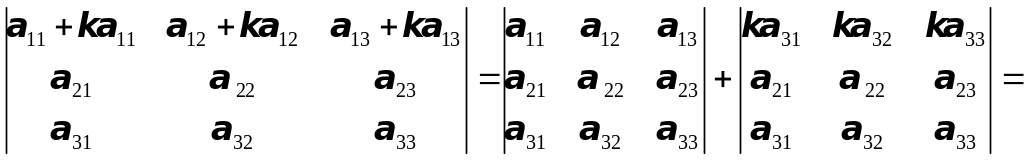
4

Определители высших порядков

Определитель квадратной матрицы n-го порядка имеет вид:

a11 a12 ... a1n

a 21 a 22 ... a 2 n

det A = A = .

... ... ... ...

a n1 an 2 ... a nn

Для определителей n-го порядка справедливы свойства, изложенные в

разделе 1.3.

Определители n-го порядка могут быть вычислены двумя способами.

1. Метод разложения по строке или столбцу (метод понижения порядка):

n

det A = A = ∑ aik Aik = ai1 Ai1 + ai 2 Ai 2 + ...ain Ain .

k =1

ПРИМЕР:

2 −1 0 1

0 1 −1 2

Вычислим определитель 4-го порядка A= методом понижения

3 −1 3 2

3 1 1 6

порядка.

Решение:

Обозначим строки определителя через α1 , α 2 , α3 , α 4 , а столбцы - β1 , β 2 , β 3 , β 4 .

Приведем определитель к виду, в котором a11 = 1 , а остальные элементы первого

столбца равны нулю. Для этого поставим четвертый столбец на место первого,

при этом определитель изменит знак:

1 −1 0 2

2 1 −1 0

A =− .

2 −1 3 3

6 1 1 3

Обратим в нули элементы первого столбца во второй, третьей и четвертой

строках с помощью преобразований α 2 − 2α1 , α3 − 2α1 , α 4 − 6α1 :

11

1 −1 0 2

3 −1 −4

0 3 −1 −4

A =− = − 1 3 −1 =

0 1 3 −1

7 1 −9

0 7 1 −9

1 3 −1 1 3 −1

⎛ α 2 − 3α1 ⎞ 10 −1

= (α 2 → α1 ) 3 −1 −4 =⎜ ⎟ 0 −10 −1 = = 0.

7 1 −9 ⎝ α 3 − 7α1 ⎠ 0 −20 −2 20 −2

2. Метод приведения к треугольному виду.

Используя свойства, добьемся такой структуры определителя, при которой

все его элементы, стоящие ниже главной диагонали, равны нулю. Тогда оп-

ределитель будет численно равен произведению элементов, стоящих на главной

диагонали.

a11 a12 ... a1n

0 a22 ... a2 n n

A→ , A = ∏ aii =a11 ⋅ a22 ⋅ ...⋅ ann .

... ... ... ... i =1

0 0 ... ann

ПРИМЕР:

1 0 2 1 3

4 −1 3 2 5

Вычислим определитель 5-го порядка Α = −3 2 −4 5 −7 методом приве-

2 3 19 5 8

5 −3 −5 −1 4

дения к треугольному виду.

Решение:

1 0 2 1 3 (α 1 )

⎛ α − 4α 1 ⎞

4 −1 3 2 5 (α 2 ) ⎜ 2 ⎟

Α = −3 2 −4 5 −7 ⎜ α 3 + 3α 1 ⎟ =

(α 3 ) = ⎜

α − 2α 1 ⎟

2 3 19 5 8 (α 4 ) ⎜ 4 ⎟

⎝ α 5 − 5α 1 ⎠

5 −3 −5 −1 4 (α 5 )

1 0 2 1 3 (α1 ) 1 0 2 1 3 (α1 )

0 −1 − 5 − 2 − 7 ( α 2 ) 0 −1 − 5 − 2 − 7 ( α 2 )

= 0 2 2 8 2 (α 3 ) = (α 5 + α 4 ) = 2 ⋅ 0 1 1 4 1 (α 3 ) =

0 3 15 3 2 (α 4 ) 0 3 15 3 2 (α 4 )

0 −3 −15 −6 −11 (α5 ) 0 0 0 −3 − 9 (α 5 )

5

6

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.