
- •§ 3. Основные свойства определителей 3-го порядка.
- •Тогда, используя свойство 5, а затем 4, будем иметь
- •Свойства обратной матрицы
- •Матричный метод решения систем линейных уравнений
- •Алгоритм
- •[Править] Пример
- •Компланарные векторы
- •Бесконечно малая величина
- •[Править] Бесконечно большая величина
- •Предел последовательности и функции. Теоремы о пределах
- •Бесконечно малые функции
- •Свойства бесконечно малых функций
- •Бесконечно большие функции
- •Свойства бесконечно больших функций в точке
- •Пределы функции на бесконечности
- •Определения Править
- •Окрестностное определение Править
- •Определения Править
- •Определения
- •[Править] Односторонний предел по Гейне
- •[Править] Односторонний предел по Коши
- •[Править] Односторонний предел как предел вдоль фильтра
- •[Править] Обозначения
- •Построение асимптот при анализе функций
- •Примеры:
- •Точки разрыва
- •Непрерывность функции в точке
- •Свойства непрерывных функций
- •Свойства непрерывных функций. Непрерывность сложной функции
- •Теоремы о непрерывных функциях
- •Непрерывность обратной функции
- •Непрерывность функций
- •[Править] Доказательство
- •Формулировка
- •[Править] Доказательство для r
- •[Править] Замечания
- •Второй замечательный предел
- •Натуральные логарифмы
- •Свойства Править
- •Дифференцирование сложной функции
- •[Править] Примеры
- •[Править] Свойства
- •[Править] Разложение в степенной ряд
- •Теорема об обратной функции.
- •Теорема (о дифференцировании обратной функции)
- •Примеры
- •Дифференцирование функций заданных параметрически
- •36. Логарифмическое дифференцирование.
- •Правила отыскания производных показательных и логарифмических функций.
- •Производные обратных тригонометрических функций
- •Теорема Ролля
- •Геометрический смысл теоремы Ролля
- •Теорема Лагранжа
- •Геометрический смысл теоремы Лагранжа
- •Теорема Коши
Пределы функции на бесконечности
Править
История
Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю.
Определения Править
Пусть задана числовая функция с неограниченной сверху областью определения, то есть
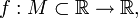 и
и
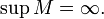 Число
Число
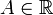 называется
пределом функции f
при x
стремящемся к бесконечности, если
называется
пределом функции f
при x
стремящемся к бесконечности, если
![]()
Пишут:
![]()
Аналогично пусть и
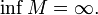 Число
называется
пределом функции f
при x
стремящемся к минус бесконечности,
если
Число
называется
пределом функции f
при x
стремящемся к минус бесконечности,
если
![]()
Пишут:
![]()
Окрестностное определение Править
Расширенная
числовая прямая
![]() становится
топологическим пространством, если её
снабдить естественной топологией,
определив окрестности ьдьщых точек
следующим образом:
становится
топологическим пространством, если её
снабдить естественной топологией,
определив окрестности ьдьщых точек
следующим образом:
Окрестностью точки
 является
любой интервал
является
любой интервал
![]()
Окрестностью точки
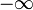 является
любой интервал
является
любой интервал
![]()
Пределы функции на бесконечности тогда можно определить как обычные пределы на топологическом пространстве.
Число A называется пределом функции f при x стремящемся к бесконечности, если для любой окрестности V(A) существует окрестность
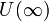 такая,
что
такая,
что
![]()
Число A называется пределом функции f при x стремящемся к минус бесконечности, если для любой окрестности V(A) существует окрестность
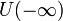 такая,
что
такая,
что
![]()
Преде́л фу́нкции — одно из основных понятий математического анализа. Функция f(x) имеет предел A в точке x0 если для всех значений x, достаточно близких к x0, значение f(x) близко к A.
Содержание [показать]
|
Определения Править
(определение по Коши, ε−—определение) Пусть дана функция
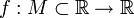 и
и
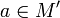 —
предельная
точка
множества
M.
Число
называется
пределом функции f
при x,
стремящемся к a
—
предельная
точка
множества
M.
Число
называется
пределом функции f
при x,
стремящемся к a
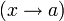 ,
если
,
если
![]()
(окрестностное определение) Пусть дана функция и — предельная точка множества M. Число называется пределом функции f при x, стремящемся к a , если для любой окрестности V(A) точки A существует проколотая окрестность
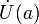 точки
a
такая, что
точки
a
такая, что
![]()
(определение по Гейне) Пусть дана функция и — предельная точка множества M. Будем называть
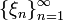 последовательностью
Гейне,
если
последовательностью
Гейне,
если
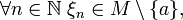 и
и
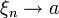 при
при
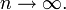 Число
называется
пределом функции f
при x,
стремящемся к a
тогда
и только тогда, когда для любой
последовательности Гейне имеем
Число
называется
пределом функции f
при x,
стремящемся к a
тогда
и только тогда, когда для любой
последовательности Гейне имеем
![]() при
при
66
Определения
Пусть
на некотором числовом
множестве
![]() задана
числовая
функция
задана
числовая
функция
![]() и
число
и
число
![]() —
предельная
точка
области
определения
—
предельная
точка
области
определения
![]() .
Существуют различные определения для
односторонних пределов функции
.
Существуют различные определения для
односторонних пределов функции
![]() в
точке
,
но все они эквивалентны.
в
точке
,
но все они эквивалентны.
