Свойства обратной матрицы

• , где 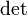обозначает определитель.

• для любых двух обратимых матриц A и B.

• где * ^T обозначает транспонированную матрицу.

• для любого коэффициента .

• Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1} существует, то x = A ^{− 1}b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

7

Матричный метод решения систем линейных уравнений

            Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

            Метод удобен для решения систем невысокого порядка.

            Метод основан на применении свойств умножения матриц. 

            Пусть дана система уравнений: 

Составим матрицы:   A = ;             B = ;           X = . 

Систему уравнений можно записать:

AX = B. 

Сделаем следующее преобразование: A^-1AX = A^-1B,  

т.к.   А^-1А = Е, то  ЕХ = А^-1В

Х = А^-1В

            Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.

            Пример. Решить систему уравнений:

Х = , B = , A =

Найдем обратную матрицу А^-1.

 = det A = 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.

 

M₁₁ =  = -5;                  M₂₁ =  = 1;                   M₃₁ =    = -1;

M₁₂ =                M₂₂ =                     M₃₂ =

M₁₃ =                  M₂₃ =                     M₃₃ =

 

                     A^-1 = ; 

Cделаем проверку:

AA^-1 = =E.

Находим матрицу Х.

Х = = А^-1В =  = .

 

Итого решения системы: x =1; y = 2; z = 3.

8

Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2].

Пример

Покажем, как методом Гаусса можно решить следующую систему:

Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на и , соответственно:

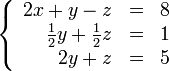
Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на :

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

из третьего;

из второго, подставив полученное

из первого, подставив полученные и .

9

Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана^[1].

Алгоритм

1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.

2. Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.

3. Все элементы первой строки делят на верхний элемент выбранного столбца.

4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

6. После повторения этой процедуры n − 1 раз получают верхнюю треугольную матрицу

7. Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.