33. Уравнения прямой в двухмерном пространстве.
Пусть даны две точки M0(x0, y0) и M1(x1, y1). Требуется написать уравнение прямой, проходящей через эти точки. Для случая плоскости канонические уравнения примут вид:
.
Вектор
может быть взят в качестве направляющего
вектора прямой. И, следовательно,
уравнение прямой, проходящей через две
заданные точки M0 и M1, примет вид
.
Запишем параметрические уравнения прямой
.
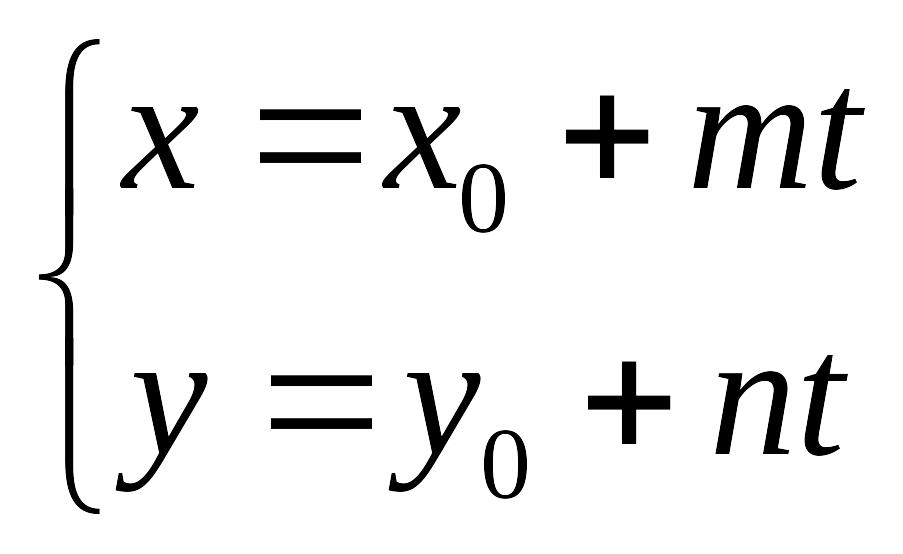Пусть прямая не перпендикулярна оси Ох, т.е. m ≠0, тогда, исключив параметр t из уравнений, получаем
,
где
.
Уравнение называют уравнением прямой, проходящей через точку M0(x0, y0) и имеющей угловой коэффициент k.
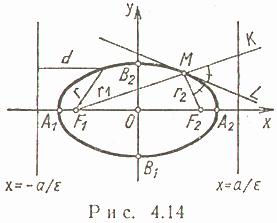
34. Кривые второго порядка. Эллипсы.
Кривой второго порядка называется линия на плоскости, описываемая уравнением второй степени относительно переменных x и y, т.е.
,
где
-
некоторые константы.
Каноническое уравнение эллипса имеет вид
Любое уравнение
вида со значениями коэффициентов
определяет на плоскости эллипс и может
быть представлено в виде
.
Числа
и
называются, соответственно, большой и
малой полуосями эллипса. Точки
и
,
где
,
называются фокусами эллипса. Точки
называются вершинами эллипса.
Характеристическое свойство эллипса: для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянная, равная 2а.
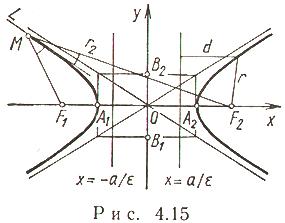
35. Кривые второго порядка. Гиперболы.
Кривой второго порядка называется линия на плоскости, описываемая уравнением второй степени относительно переменных x и y, т.е.
,
где - некоторые константы.
Каноническое уравнение гиперболы имеет вид
Любое уравнение
вида со значениями коэффициентов
определяет на плоскости гиперболу и
может быть представлено в виде
.
Числа
и
называются, соответственно, действительной
и мнимой полуосями гиперболы. Точки
и
,
где
,
называются фокусами гиперболы. Точки
называются вершинами гиперболы. Прямые,
заданные уравнениями
,
являются асимптотами гиперболы.
Характеристическое свойство гиперболы: для любой точки гиперболы разность расстояний этой точки до фокусов по абсолютной величине есть величина постоянная, равная 2а.
Гипербола с
уравнением
или
называется сопряженной к гиперболе с
уравнением
,
имеет тот же осевой прямоугольник и
асимптоты, но пересекает ось OY в точках
и фокусы лежат на оси OY.
36. Уравнение прямой в трехмерном пространстве.
П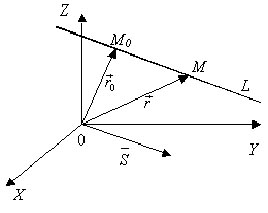
рямую
линию можно определить как геометрическое
место точек, принадлежащих одновременно
двум непараллельным плоскостям. Пусть
уравнения плоскостей P1 и P2 заданы, тогда
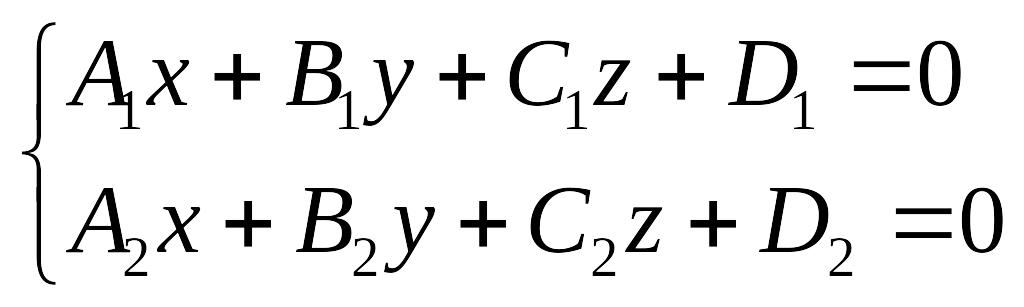
определяет прямую линию, и систему называют общим уравнением прямой линии.
Рассмотрим теорию
прямой линии в пространстве R3. Очевидно,
прямая линия будет полностью определена,
если на ней фиксировать точку M0(x0, y0, z0)
и вектор
,
параллельный этой прямой. Точку M0 иногда
называют начальной точкой, а вектор
- направляющим вектором прямой. Получим
наиболее употребительные формы уравнения
прямой в пространстве.
Пусть
- радиус-вектор начальной точки M0,
-
радиус-вектор текущей точки М прямой.
Тогда вектор
коллинеарен направляющему вектору
прямой
,
следовательно,
,
где t - некоторое
число, называемое параметром. Уравнение
называется векторным параметрическим
уравнением прямой. Если
,
.
,
то можно перейти от уравнения к
параметрическим уравнениям прямой в
координатном виде:
Изменяя значения t, можно получить координаты любой точки, лежащей на прямой. Из уравнений получим:
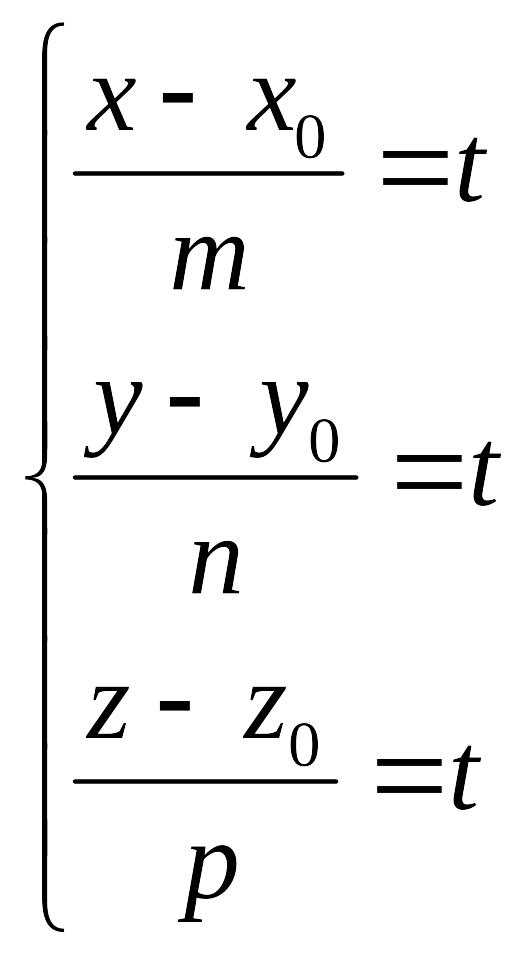
Отсюда
.
Уравнения называются каноническими уравнениями прямой.