15. Модель многоотраслевой экономики Леонтьева.

Предположим, что рассматривается n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.

Введем следующие обозначения:

x_i - общий (валовой) объем продукции i-й отрасли (i = 1,2,...,n);

x_ij - объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства (i,j = 1,2,...,n);

y_i - объем конечного продукта i-й отрасли для непроизводственного потребления.

Так как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями и конечного продукта, то

x_i = (x_i1 + x_i2+ ... + x_in) + y_i , (i = 1,2,...,n).

Эти уравнения (их n штук) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в эти уравнения, имеют стоимостное выражение.

Введем коэффициенты прямых затрат:

a_ij = x_ij / x_j , (i,j = 1,2,...,n),

показывающие затраты продукции i-й отрасли на производство единицы стоимости j-й отрасли.

Можно полагать, что в некотором промежутке времени коэффициенты a_ij будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.

x_ij = a_ijx_j , (i,j = 1,2,...,n),

вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной.

Теперь соотношения баланса примут вид:

x_i = (a_i1x₁ + a_i2x₂ + ... + a_inx_n) + y_i , (i = 1,2,...,n),

Обозначим

, , ,

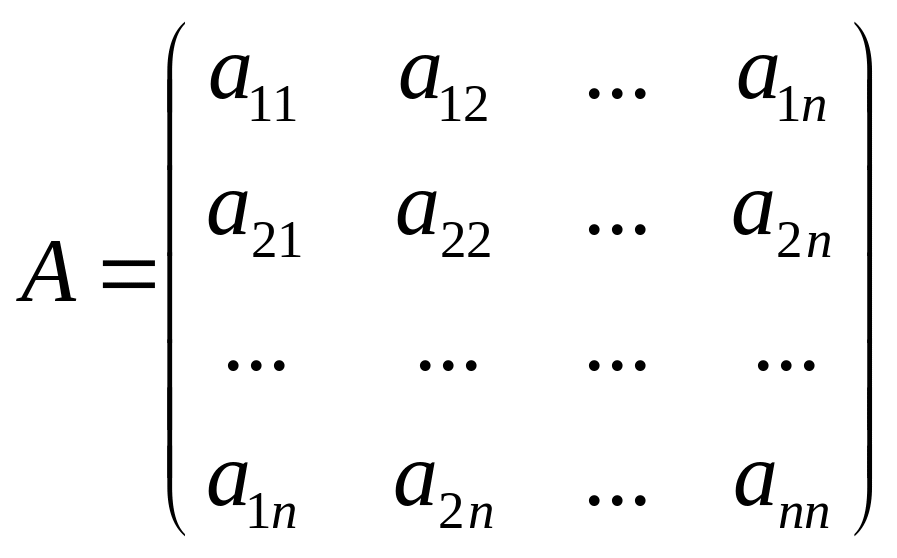где

X - вектор валового выпуска;

A - матрица прямых затрат (технологическая или структурная матрица);

Y - вектор конечного продукта.

Тогда соотношения баланса можно записать в виде:

X = AX + Y.

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта Y.

Перепишем матричное уравнение в виде:

(E - A) X = Y.

Если матрица (E - A) невырожденная, т.е. ее определитель не равен нулю, тогда:

X = (E - A)^-1 Y.

Матрица S = (E - A)^-1 называется матрицей полных затрат.

Чтобы выяснить экономический смысл элементов матрицы S = (s_ij), будем задаваться единичными векторами конечного продукта:

, , …, .

Тогда соответствующие векторы валового выпуска будут:

, , …, .

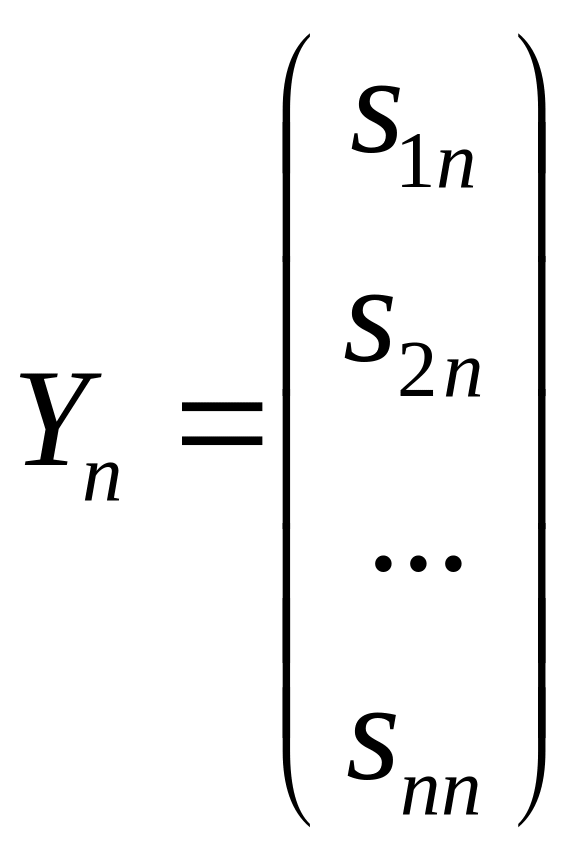Следовательно, каждый элемент s_ij матрицы S есть величина валового выпуска продукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли.

В соответствии с экономическим смыслом задачи значения x_i должны быть неотрицательны при неотрицательных значениях y_i и a_ij.

Матрица А называется продуктивной, если для любого вектора Y существует решение X уравнения (E - A) X = Y. В этом случае и модель Леонтьева называется продуктивной.

16. Линейное пространство.

Пусть V - непустое множество (его элементы будем называть векторами и обозначать ...), в котором установлены правила:

1) любым двум элементам соответствует третий элемент , называемый суммой элементов (внутренняя операция);

2) каждому и каждому отвечает определенный элемент (внешняя операция).

Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:

I. ,

II. ,

III. (нулевой элемент, такой, что , ).

IV. (элемент, противоположный элементу ), такой, что .

V. , .

VI. , ,

VII. , ,

VIII. , ,