12. Вычисление обратной матрицы методом Гаусса.

Вычисление обратной матрицы методом Гаусса заключается в том, что любую неособенную матрицу А путем элементарных преобразований только столбцов (или только строк) можно привести к единичной матрице Е, и если совершенные над матрицей А элементарные преобразования в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать элементарные преобразования над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. При отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

Пример. Методом исключения Гаусса найдем матрицу, обратную к матрице

Решение:

К матрице А справа приписывается единичная матрица того же порядка (А|E)

Матрица (А|E) приводится элементарными преобразованиями первого и второго типов к ступенчатому виду

13. Системы линейных однородных уравнений. Свойства. Фундаментальное решение.

В общем виде система n линейных однородных алгебраических уравнений запишется

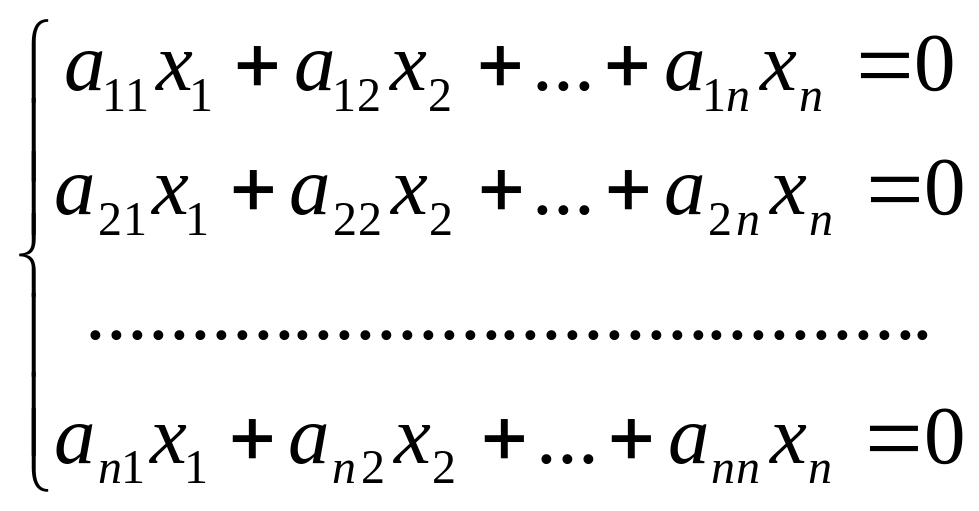
Очевидно, такая система имеет нулевое (тривиальное) решение

Если ∆ ≠ 0, то такая система имеет единственное решение, корни которого . Других ненулевых решений нет.

Если ∆ = 0, то так как все вспомогательные определители системы равны нулю, то система имеет бесконечное множество решений.

Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

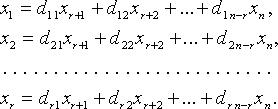
Тогда n - r линейно независимыми вектор-решениями будут:

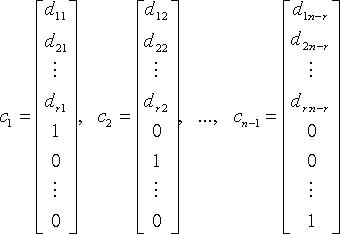
а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.

14. Общее решение системы линейных алгебраических уравнений. Свободные неизвестные. Базисные решения.

Рассмотрим однородную линейную систему

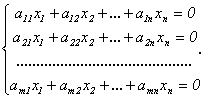
Отметим, что такая система всегда совместна, поскольку имеет нулевое решение называемое тривиальным.

Пусть ранг матрицы системы r<n. Предположим, что в базисный минор входят коэффициенты первых r уравнений. Тогда оставшиеся m – r уравнений являются линейными комбинациями, то есть следствиями предыдущих. Поэтому можно оставить в системе только первые r уравнений:

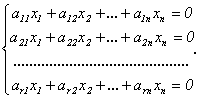
Оставим в левой части каждого уравнения неизвестные, коэффициенты при которых входят в базисный минор, а остальные неизвестные перенесем направо:

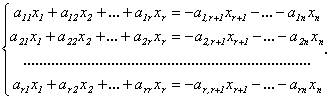
Эта система будет иметь единственное решение относительно неизвестных выражающее их через остальные неизвестные ( ), которым можно придавать любые произвольные значения. Таким образом, система при r<n является неопределенной.

Неизвестные коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные ( ) –свободными неизвестными.

Решения системы называются линейно независимыми, если линейная комбинация дает нулевой столбец только при