5. Непрерывность функции. Точки разрыва 1 и 2 рода.

Функция называется непрерывной в точке х=а, если её предел в этой точке существует и равен f(a).

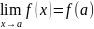
Предел слева: 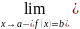, если последовательность значений у₁= f(x₁), у₂= f(x₂)…сходится к числу b для любой последовательности x₁, х₂..сходящейся к точке а слева (т.е. x₁, х₂<а)

Предел справа определяется также.

Пусть функция f(x) определена в некоторой окрестности точки х=а (возможно, кроме самой точки а). Тогда а называется точкой разрыва 1 рода, если левый и правый пределы в точке а существуют, но не равны. И точка а называется точкой разрыва 2 рода, если хотя бы один из односторонних пределов не существует или бесконечен.

6. Свойства непрерывных функций

Функция f(x) непрерывна на отрезке 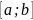, если она непрерывна в каждой внутренней точке С (т.е. а< с<b)

и , .

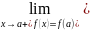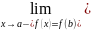Примеры: а) f(x)=х² непрерывна на любом отрезке. б) f(x)= непрерывна на любом отрезке, не содержащем точку х=0. Но разрывна на , если а< 0 < b.

Теорема 1. Пусть функция f(x) непрерывна на отрезке и принимает на его концах разные по знаку значения (т.е. f(a)<0; f(b)˃0 или f(a)˃0; f(b)<0). Тогда на отрезке найдется такая точка С, что f(c)=0.

Теорема 2. Пусть функция f(x) непрерывна на отрезке и f(a)=A, f(b)=B. Пусть, например, А<В. Тогда на отрезке функция f(x) принимает и все промежуточные значения между А и В, т.е. для любого числа Т€ найдется t€ , такое, что f(t)=T.

Теорема 3. Если функция f(x) непрерывна на отрезке , то она достигает на нем своего наибольшего и наименьшего значения.

Примеры: а) f(x)=x², =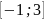 , max в точке х=3, minв точке х=0.

б) f(x)= = . На этом отрезке функция разрывна, поэтому max не достигается, а min в точке х=1

7. Производная функции. Геометрический и физический смысл производной.

Производной функции в точке х называется предел: f(x)= или y’= 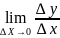если такой предел существует.

Пример: f(x)=x. Тогда f(x + ∆x) = x +∆x. Поэтому f(x + ∆x) - f(x)= (x + ∆x)- х = ∆x и = 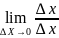= 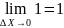. Следовательно (x)’=1

Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том, что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке х_o; физический смысл - в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t₀.

Геометрический смысл: f’(x)= tgα минус значение производной в точке х = тангенсу угла наклона к графику функции.

Физический смысл: Пусть переменная t обозначает время, а S= S(t) – путь, пройденный за время t. Тогда ∆S= S(t+∆t) – S(t) – путь, пройденный за промежуток времени (t,t+∆t). Отсюда следует, что средняя скорость движения в промежутке времени (t,t+∆t) равно 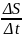. Отсюда следует, что физический смысл производной – это мгновенная скорость в момент t: V(t)=S(t).

8. Дифференциал функции. Основные правила дифференцирования.

Нахождение производной называется дифференцированием функции.

Дифференциал: d(y) = f’(x) dx ⇒ f’(x) =

Основные правила дифференцирования:

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) (uv)' = u'v+v'u;

4)