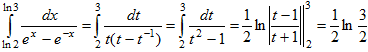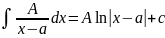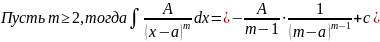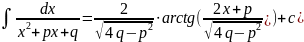- •Функции и способы их задания. Элементарные функции
- •Предел последовательности. Сходящиеся и расходящиеся последовательности.
- •Определение предела функции. Примеры.
- •Основные свойства пределов. Замечательные пределы.
- •Непрерывность функции. Точки разрыва 1 и 2 рода.
- •Свойства непрерывных функций
- •Производная функции. Геометрический и физический смысл производной.
- •Дифференциал функции. Основные правила дифференцирования.
- •9) Основные правила дифференциального исчисления.
- •10 ) Правило Лопиталя. Формулы Тейлора и Маклорена.
- •11) Исследование функции с помощью дифференциального исчисления.
- •12) Функции нескольких переменных. Частные производные.
- •13) Условный экстремум. Метод множителей Лагранжа.
- •14) Неопределенный интеграл и его основные свойства.
- •15) Замена переменных и интегрирование по частям для неопределенного интеграла.
- •16) Интегрирование рациональных функций.
- •17) (Подписать к графику!!) Интегральная сумма и определенный интеграл.
- •18) Основные свойства определенных интегралов. Методы интегрирования.
- •19) Геометрические приложения определенного интеграла.
- •1) Вычисление площади плоских фигур
- •2) Вычисление объема
- •20) Приближенное вычисление определенного интеграла. Методы интегрирования.
- •1) Формула прямоугольников
- •2) Формула трапеции
- •21) Дифференциальные уравнения. Примеры задач, приводящих к дифференциальным уравнениям.
- •22) Задача Коши и теорема Коши.
- •23) Дифференциальные уравнения с разделяющимися переменными.
- •24) Решение дифференциальных уравнений методом подстановки (метод Бернулли)
- •Первый способ
- •Второй способ
- •25) Решение дифференциальных уравнений методом вариации постоянной (метод Лангранжа) Метод вариации постоянной (метод Лагранжа)
15) Замена переменных и интегрирование по частям для неопределенного интеграла.
Формулы замены переменных:
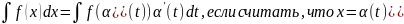
Пример:
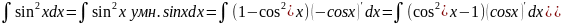
Вводим
новую переменную t=cosx.
Тогда
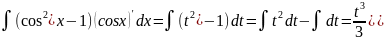 - t
+ C=
- t
+ C=

Интегрирование по частям:
Пусть даны две функции U(x) и V(x). Тогда:
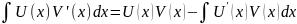 (упрощенный
вариант …= UV-
(упрощенный
вариант …= UV-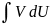
Пример:
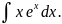 Обозначим U=x,
V=
Обозначим U=x,
V= ,
V’=
,
V’=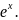 Поэтому
Поэтому
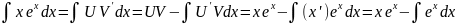 =
=
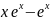 +C.
+C.
16) Интегрирование рациональных функций.
Опр.
Рациональная функция (или рац. дробь) –
это функция вида
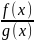 ,
где f(x)
и g(x)
– многочлены от x
,
где f(x)
и g(x)
– многочлены от x
Примеры:
x;
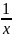 ; x2-1;
; x2-1;
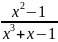
Опр. Рациональная дробь называется правильной, если степень многочлена f(x) меньше степени g(x).
Опр. Простейшие рациональные дроби – это дробь вида
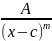 ,
m>1 целое, A
и C
– постоянные
,
m>1 целое, A
и C
– постоянные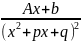 ,
где p2-4q<0(многочлен
,
где p2-4q<0(многочлен
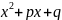 не имеет корней.
не имеет корней.
Теорема. Всякая рациональная дробь является суммой многочлена и правильной дроби. Любая правильная дробь разлагается в сумму простейших дробей.
Пример: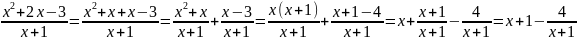
Интегрирование некоторых простейших дробей:
Интегрировать рациональные функции можно выражая через простейшие дроби.
Пример:
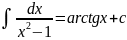 ,
так как
,
так как
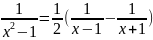
17) (Подписать к графику!!) Интегральная сумма и определенный интеграл.
![]() -
называется интегральной суммой
-
называется интегральной суммой
функции f(x) на отрезке [a;b]
эта сумма равна суммые интеграций прямоугольников(см рисунок) и приближенно равна площади над кривой y=f(x) (см рисунок)
чем мельче разбиения ,тем меньше интегральная сумма отличается от площади криволинейной фигуры,ограниченной графиком функции y=f(x) сверху, осью Ох снизу и вертикальными прямыми х=а, х=в.

Определенный интеграл
Предел интегральной суммы Sn при λ→0 называется определенным интегралом функции f(x) на отрезке [a;b]
Обозначение

18) Основные свойства определенных интегралов. Методы интегрирования.
Основные св-ва определенного интеграла:
I.
Величина определенного интеграла не
зависит от обозначения переменной
интегрирования, т.е. ![]() ,
где х, t – любые буквы.
,
где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
![]()
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
![]()
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
![]()
V. Постоянный множитель можно выносить за знак определенного интеграла.
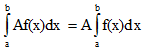
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
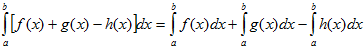
Методы интегрирования:
1) Основной формулой интегрального исчисления является так называемая формула Ньютона-Лейбница.
ТЕОРЕМА. Пусть функция у=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная для f(x) на [a,b]. Тогда определенный интеграл от функции f(x) на [a,b] равен приращению первообразной F(x) на этом отрезке, т.е.
![]() (2)
(2)
Нахождение определенных интегралов с использованием формулы Ньютона–Лейбница (2) осуществляется в два шага: на первом шаге, используя технику нахождения неопределенного интеграла, находят некоторую первообразную F(x) для подынтегральной функции f(x); на втором применяется собственно формула Ньютона-Лейбница – находится приращение первообразной, равное искомому интегралу. В связи с этим, введем обозначение для приращения первообразной, которое удобно использовать при записи решений. По определению положим
![]() (3)
(3)
Следует подчеркнуть, что при применении формулы Ньютона – Лейбница можно использовать любую первообразную F(x) для подынтегральной функции f(x), например имеющую наиболее простой вид при С=0.
Пример
16: Вычислить определенный интеграл ![]()
Произвольная
первообразная для функции f(x)=x2 имеет
вид ![]() .
Для нахождения интеграла по формуле
Ньютона – Лейбница возьмем такую
первообразную, у которой С=0. Тогда
.
Для нахождения интеграла по формуле
Ньютона – Лейбница возьмем такую
первообразную, у которой С=0. Тогда 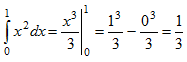
2) Метод подстановки (замена переменной)
При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.
ТЕОРЕМА.
Пусть функция φ(t) имеет непрерывную
производную на отрезке [α,β], а=φ(α), в=φ(β)
и функция f(х) непрерывна в каждой точке
х вида х=φ(t), где t [α,β].
[α,β].
Тогда справедливо следующее равенство:
Эта формула носит название формулы замены переменной в определенном интеграле.
Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).
Пример
19. Вычислить 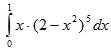
Положим
t=2-х2.
Тогда dt=d(2-х2)=(2-х2)'dx=-2xdx
и xdx=-![]() dt.
Если х=0, то t=2-02=2,
и если х=1, то t=2-12=1.
Следовательно:
dt.
Если х=0, то t=2-02=2,
и если х=1, то t=2-12=1.
Следовательно:
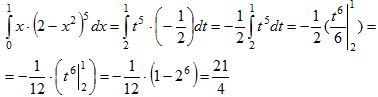
Пример
20. Вычислить ![]()
Воспользуемся
заменой переменной ![]() .
Тогда
.
Тогда ![]() и
и ![]() .
Если х=0, то t=1 и, если х=5, то t=4. Выполняя
замену, получим:
.
Если х=0, то t=1 и, если х=5, то t=4. Выполняя
замену, получим:

Пример
21. Вычислить 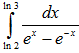
Положим t=ex. Тогда x=lnt, dx=dt/t и, если x=ln2, то t=2, если х=ln3, то t=3. Выполняя замену, получаем: