
- •Условие перпендикулярности двух векторов
- •Векторное произведение
- •Свойства [править]Геометрические свойства векторного произведения
- •[Править]Алгебраические свойства векторного произведения
- •Комплексное число
- •Определения
- •6)Решение уравнения .
- •7)Геометрическая интерпертация компл. 4исел.
- •8) Деление.
- •11) Алгоритм деления с остатком
- •12) Корни многочлена.
- •1. Сложение матриц, имеющих один и тот же размер.
- •2. Умножение матриц подходящего размера (матрицу, имеющую n строк, можно умножить справа на матрицу, имеющую n столбцов).
- •3. Умножение матрицы на элемент основного кольца или поля.
- •Теорема Лапласа
- •Векторные (линейные) пространства
- •Координаты вектора в пространстве
- •Определение линейного пространства. Изоморфизм
- •Подпространство
- •[Править]Свойства подпространств
- •Векторное пространство Определение
- •Подпространство векторного пространства
- •Матрица перехода
- •Определение
- •Характеристические корни и собственные значения
- •Собственные значения
- •Линейные преобразования с простым спектром.
- •Процесс ортогонализации Грама--Шмидта в конечномерном евклидовом пространстве
- •Уравнения прямой на плоскости
- •[Править]Общее уравнение прямой
- •12.5. Прямая линия в пространстве. Основные задачи
Матрица перехода
Координаты
вектора ![]() в
базисе
в
базисе ![]() --
это коэффициенты разложения вектора
по
базису
--
это коэффициенты разложения вектора
по
базису ![]() ,
где
,
где  .
.
Пусть
даны два базиса
и ![]() ,
причем
,
причем ![]() ,
,![]() ,
, ![]() .
.
Определение. Матрица

![]() -ый
столбец которой составлен из координат
вектора
-ый
столбец которой составлен из координат
вектора ![]() в
базисе
в
базисе ![]() ,
называетсяматрицей
перехода от
базиса
к
,
называетсяматрицей
перехода от
базиса
к ![]() .
Имеем
.
Имеем ![]() .
.
Лемма. Пусть
--
базис, а ![]() и
и ![]() --
матрицы размера
--
матрицы размера ![]() над
полем
над
полем ![]() ,
причем
,
причем![]() .
Тогда
.
Тогда ![]() .
.
Теорема. ![]() Матрица
перехода
Матрица
перехода ![]() от
базиса
к
невырождена.
от
базиса
к
невырождена.
![]() Для
любого базиса
и
любой невырожденной квадратной
матрицы
порядка
Для
любого базиса
и
любой невырожденной квадратной
матрицы
порядка ![]() существует
и при том единственный базис
с
матрицей перехода
,
т.е.
.
существует
и при том единственный базис
с
матрицей перехода
,
т.е.
.
Теорема. Если
--
матрица перехода от базиса
к
,
то для любого вектора ![]() справедливо
равенство
справедливо
равенство ![]() ,
где
,
где ![]() и
и ![]() --
столбцы координат вектора
в
базисах
и
соответственно,
т.е.
--
столбцы координат вектора
в
базисах
и
соответственно,
т.е. ![]() .
.
Определение. Биекция ![]() линейного
пространства
линейного
пространства ![]() над
полем
на
линейное пространство
над
полем
на
линейное пространство![]() над
полем
называется изоморфизмом линейных
пространств, если
над
полем
называется изоморфизмом линейных
пространств, если![]() для
любых векторов
для
любых векторов ![]() и
и ![]() .
.
Следствие. Справедливы
равенства ![]() ,
, ![]() и
и ![]() .
Если система
.
Если система ![]() линейна
независима, то система
линейна
независима, то система ![]() тоже
линейна независима. Отображение
тоже
линейна независима. Отображение ![]() --
изоморфизм.
--
изоморфизм.
Определение. Два линейных пространства называются изоморфными, если существует изоморфизм одного пространства на другое.
Теорема. Два
конечномерных пространства над
полем
изоморфны
тогда и только тогда, когда ![]() .
.
Следствие. Любое
-мерное
векторное пространство
изоморфно ![]() .
Отображение
.
Отображение![]() определено
так:
определено
так: ![]() .
.
30)
Определение
Пусть G —
заданная группа и W —
векторное пространство. Тогда представление
группы G —
это отображение, ставящее в соответствие
каждому элементу ![]() невырожденное
линейное преобразование
невырожденное
линейное преобразование ![]() причем
выполняются свойства
причем
выполняются свойства
![]()
Раздел математики, который изучает представления групп, называется теорией представлений (групп). Представление можно понимать как запись группы с помощью матриц или преобразований линейного пространства. Смысл использования представлений групп заключается в том, что задачи из теории групп сводятся к более наглядным задачам из линейной алгебры. Этим объясняется большая роль теории представлений в различных вопросах алгебры и других разделов математики. Например, одномерные представления симметрической группы Sn и знакопеременной группы An играют большую роль при доказательстве невозможности разрешения в радикалах алгебраического уравнения степени выше 4. В квантовой механике важную роль играют бесконечномерные (в которых векторное пространство — гильбертово) представления групп (в первую очередь, группы Лоренца).
Матрица линейного преобразования
В
примере 19.4 было показано, что
преобразование ![]() -мерного
пространства, заключающееся в умножении
координатных столбцов векторов на
фиксированную матрицу, является линейным
преобразованием. В этом разделе мы
покажем, что все линейные преобразования
конечномерного пространства устроены
таким же образом. Пусть
-мерного
пространства, заключающееся в умножении
координатных столбцов векторов на
фиксированную матрицу, является линейным
преобразованием. В этом разделе мы
покажем, что все линейные преобразования
конечномерного пространства устроены
таким же образом. Пусть ![]() --
-мерное
линейное пространство, в котором задан
базис
--
-мерное
линейное пространство, в котором задан
базис![]() ,
, ![]() --
линейное преобразование. Возьмем
произвольный вектор
--
линейное преобразование. Возьмем
произвольный вектор ![]() .
Пусть
.
Пусть  --
его координатный столбец. Координатный
столбец вектора
--
его координатный столбец. Координатный
столбец вектора![]() обозначим
обозначим ![]() .
Запишем разложение вектора
по
базису пространства
.
Запишем разложение вектора
по
базису пространства![]() .
Для образа этого вектора получим
.
Для образа этого вектора получим (
19 .2) Векторы
(
19 .2) Векторы ![]() имеют
какие-то координатные столбцы, обозначим
их
имеют
какие-то координатные столбцы, обозначим
их  ,
,  ,
...,
,
...,  соответственно.
В этой записи первый индекс показывает
номер координаты, а второй индекс --
номер вектора. Соответственно,
соответственно.
В этой записи первый индекс показывает
номер координаты, а второй индекс --
номер вектора. Соответственно,  Подставим
это выражение в равенство ( 19.2 ) и,
используя предложение 14.3 , изменим
порядок суммирования
Подставим
это выражение в равенство ( 19.2 ) и,
используя предложение 14.3 , изменим
порядок суммирования Это
равенство означает, что
Это
равенство означает, что ![]() -той
координатой вектора
служит
-той
координатой вектора
служит  .
Составим матрицу
.
Составим матрицу ![]() из
координатных столбцов векторов
из
координатных столбцов векторов ![]() ,
...,
,
..., ![]()
 Вычислим
произведение матрицы
на
столбец
Вычислим
произведение матрицы
на
столбец ![]()
 Мы
видим, что
-ый
элемент столбца совпадает с
-ой
координатой вектора
.
Поэтому
Мы
видим, что
-ый
элемент столбца совпадает с
-ой
координатой вектора
.
Поэтому ![]() (
19 .3) Это означает, что в выбранном базисе
действие любого линейного преобразования
сводится к умножению матрицы на
координатный столбец вектора.
Матрица
называется
матрицей линейного преобразования
.
Еще раз напомним, как она составлена:
первый столбец является координатным
столбцом образа первого базисного
вектора, второй столбец -- координатным
столбцом образа второго базисного
вектора и т.д. Пример
19 . 5 Найдем матрицу линейного
преобразования
из
примера 19.1 . Выберем какой-нибудь
базис
(
19 .3) Это означает, что в выбранном базисе
действие любого линейного преобразования
сводится к умножению матрицы на
координатный столбец вектора.
Матрица
называется
матрицей линейного преобразования
.
Еще раз напомним, как она составлена:
первый столбец является координатным
столбцом образа первого базисного
вектора, второй столбец -- координатным
столбцом образа второго базисного
вектора и т.д. Пример
19 . 5 Найдем матрицу линейного
преобразования
из
примера 19.1 . Выберем какой-нибудь
базис ![]() .
Тогда
.
Тогда![]() Следовательно,
первый столбец матрицы
имеет
вид
Следовательно,
первый столбец матрицы
имеет
вид .
Аналогично
.
Аналогично ![]() Второй
столбец матрицы
имеет
вид
Второй
столбец матрицы
имеет
вид  .
В итоге
.
В итоге  Пример 19 . 6
Найдем матрицу линейного преобразования
из
примера 19.2 . Угол
Пример 19 . 6
Найдем матрицу линейного преобразования
из
примера 19.2 . Угол ![]() возьмем
равным
возьмем
равным ![]() .
В качестве базиса возьмем привычный
ортонормированный базис i , j . Из рисунка
19.7 видно, что вектор
.
В качестве базиса возьмем привычный
ортонормированный базис i , j . Из рисунка
19.7 видно, что вектор ![]() имеет
координаты
имеет
координаты ![]() и
и ![]() .
. Рис.
19 . 7 .Координаты образов базисных векторов
при преобразовании поворота Поэтому
координатный столбец образа первого
базисного вектора имеет вид
Рис.
19 . 7 .Координаты образов базисных векторов
при преобразовании поворота Поэтому
координатный столбец образа первого
базисного вектора имеет вид 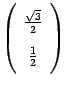 .
Координаты образа второго базисного
вектора равны
.
Координаты образа второго базисного
вектора равны ![]() и
и ![]() ,
его координатный столбец имеет вид
,
его координатный столбец имеет вид .
В итоге получаем, что в базисе i , j матрица
поворота на угол
имеет
вид
.
В итоге получаем, что в базисе i , j матрица
поворота на угол
имеет
вид 
31)
Характеристический многочлен матрицы — это многочлен, определяющий её собственные значения.
