[Править]Алгебраические свойства векторного произведения

Представление	Описание
	свойство антикоммутативности
	свойство ассоциативности относительно умножения на скаляр
	свойство дистрибутивности по сложению
	тождество Якоби, выполняется в   и нарушается в
	формула «БАЦ минус ЦАБ», тождество Лагранжа
	Это частный случай мультипликативности   нормы кватернионов
	значение этого выражения называют смешанным произведением векторов a, b, c и обозначают 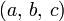  либо

Условия параллельности и перпендикулярности векторов      Так как скалярное произведение двух перпендикулярных векторов   и   равно 0, то условием перпендикулярности отличных от нуля векторов будет равенство  .      При умножении вектора   на скаляр   получаем вектор   одного направления с   при λ > 0и противоположного направления при λ < 0. Но всегда векторы   будут параллельны.      Поэтому условием параллельности векторов   будет пропорциональность их соответствующих координат:  .

3)

1.16. Смешанное произведение векторов и его свойства

Смешанным произведением векторов   называется число  , равное скалярному произведению вектора   на векторное произведение векторов   и  . Смешанное произведение обозначается  .

Геометрические свойства смешанного произведения

1. Модуль смешанного произведения некомпланарных векторов   равен объему   параллелепипеда, построенного на этих векторах. Произведение   положительно, если тройка векторов   — правая, и отрицательно, если тройка   — левая, и наоборот.

2. Смешанное произведение   равно нулю тогда и только тогда, когда векторы   компланарны:

 векторы   компланарны.

Докажем первое свойство. Найдем по определению смешанное произведение: , где   — угол между векторами   и  . Модуль векторного произведения (по геометрическому свойству 1) равен площади   параллелограмма, построенного на векторах   и  : . Поэтому  . Алгебраическое значение   длины проекции вектора   на ось, задаваемую вектором  , равно по модулю высоте   параллелепипеда, построенного на векторах   (рис. 1.47). Поэтому модуль смешанного произведения равен объему   этого параллелепипеда:

Знак смешанного произведения определяется знаком косинуса угла  . Если тройка   правая, то   и смешанное произведение   положительно. Если же тройка   левая, то   и смешанное произведение   отрицательно.

Докажем второе свойство. Равенство  возможно в трех случаях:   или   (т.е.  ),или   (т.е. вектор   принадлежит плоскости векторов   и  ). В каждом случае векторы   компланарны (см. разд. 1.1).

Алгебраические свойства смешанного произведения

1. При перестановке двух множителей смешанное произведение изменяет знак на противоположный:

При циклической (круговой) перестановке множителей смешанное произведение не изменяется:

2. Смешанное произведение линейно по любому множителю.

Первое свойство следует из геометрического свойства 1 и свойств ориентации троек векторов (см. разд. 1.9), поскольку от перестановки двух множителей модуль смешанного произведения не изменяется, а меняется только ориентация тройки. При циклической перестановке векторов ориентация тройки не изменяется.

Второе свойство следует из линейности скалярного произведения и свойства 1.

Пример 1.21. Объем параллелепипеда, построенного на векторах  , равен  . Найти объем параллелепипеда, построенного на векторах .

Решение. Используя алгебраические и геометрические свойства, найдем смешанное произведение

а затем его модуль  . По первому геометрическому свойству смешанного произведения искомый объем равен  .

Теорема 1.9 (формула вычисления смешанного произведения). Если векторы   в правом ортонормированном базисе   имеют координаты  ;  ;   соответственно, то смешанное произведение этих векторов находится по формуле

В самом деле, учитывая (1.10) и (1.15), по определению находим:

что и требовалось доказать.

4)