Теорема Лапласа

Теорема 1. (Теорема Лапласа) Зафиксируем в квадратной матрице   произвольные   строк с номерами  . Тогда определитель матрицы   равен сумме произведений всевозможных миноров, построенных на этих строках, на их алгебраическое дополнение. То есть  .

Если зафиксировать в матрице только одну строку с номером  , то, как частный случай из теоремы Лапласа, получим следующую формулу: .

Пример 6. Вычислим определитель матрицы   из примера 3 с помощью разложения по первой строке: .

17)

Свойства определителей матриц:

Свойство № 1:

Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|^Т

Следствие:

Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.

Свойство № 2:

При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

Свойство № 3:

Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

Свойство № 4:

Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

Следствия из свойств № 3 и № 4:

Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.

Свойство № 5:

Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Свойство № 6:

Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-хопределителей по формуле:

Свойство № 7:

Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Пример применения свойств для вычисления определителя матрицы:

18)

19)

Метод Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы.

Пусть имеется система уравнений:

.

Обозначим через Δ определитель матрицы системы и через Δj определитель, который получается из определителя Δ заметой j-го столбца столбцом правых частей системы ( j=1,2,...n):

.

Теорема

Если определитель матрицы отличен от нуля, т.е. Δ ≠0, то система имеет единственное решение, которое находится по формуле:

.

20)

ЛИНЕЙНОЕ ПРОСТРАНСТВО.

Множество M элементов u, v, w, ... произвольной природы, в котором определены операции сложения и умножения на число, подчиняющиеся определенным аксиомам, называется линейным пространством.

Пусть M - множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:

паре элементов множества , отвечает элемент , называемый суммой и .

Паре , отвечает элемент , называемый произведением числа и элемента .

Будем называть множество М линейным пространством, если для всех его элементов определены операции сложения и умножения на действительное число и для любых элементов и произвольных чисел справедливо:

1) (сложение коммутативно).

2) (сложение ассоциативно).

3) существует единственный нулевой элемент такой, что , .

4) для каждого элемента существует единственный противоположный элемент такой, что , .

5) (умножение на число ассоциативно).

6) .

7) ( умножение на число дистрибутивно относительно сложения элементов).

8) ( умножение вектора на число дистрибутивно относительно сложения чисел).

ВСЁ ЭТО АКСИОМЫ ЛИНЕЙНОГО ПРОСТРАНСТВА (1-8).

Линейное пространство часто называют векторным пространством, а его элементы - векторами.

Базис и размерность линейного пространства. Координаты вектора в заданном базисе.

Говорят, что вектор линейного пространства линейно выражается через векторы если его можно представить в виде линейной комбинации этих элементов, т.е. представить в виде .

Если любой вектор системы векторов линейного пространства линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой. Система векторов, которая не является линейно зависимой, называется линейно независимой.

Справедливо следующее утверждение:

Система векторов линейного пространства линейно независима тогда и только тогда, когда из равенства следует равенство нулю всех коэффициентов .

Если в линейном пространстве существует линейно независимая система из n векторов, а любая система из (n+1)-го вектора линейно зависима, то число n называется размерностью пространства . В этом случае пространство называют n-мерным линейным пространством или n-мерным векторным пространством.

Любая упорядоченная линейно независимая система n векторов линейного пространства образует базис пространства и любой вектор единственным образом выражается через векторы базиса: .

Числа называют координатами вектора в базисе и обозначают .При этом для любых двух произвольных векторов n-мерного линейного пространства , и произвольного числа справедливо: и .Это означает, что все n-мерные линейные пространства “устроены” одинаково как пространство векторов-столбцов из n действительных чисел, т.е. что все они изоморфны пространству . Линейные пространства и называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам и из соответствуют векторы и из , то вектору соответствует вектор и при любом вектору соответствует вектор .

Изоморфизм n-мерных линейных пространств пространству означает, что соотношения между элементами n-мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из и операции с ними и что всякое утверждение относительно векторов из справедливо для соответствующих элементов любого n-мерного линейного пространства.

Например, доказано, что система векторов из

, ,..

образует базис в тогда и только тогда, когда отличен от нуля определитель матрицы, со столбцами :

.

Для векторов из это означает, что они образуют базис в тогда и только тогда, когда отличен от нуля определитель матрицы, столбцами которой являются компоненты векторов .

Пусть и - два базиса в . Матрицей перехода от базиса к базису называется матрица С , столбцами которой являются координаты векторов в базисе :

…

• , .

Вектор линейно выражается через векторы обоих базисов. Тогда, если , то координаты вектора в базисе , и его координаты в базисе связаны соотношениями

.

21)

Линейная зависимость и линейная независимость строк (столбцов) матрицы.

Столбец называется линейной комбинацией столбцов одинаковых размеров, если где — некоторые числа. В этом случае говорят, что столбец разложен по столбцам , а числа называют коэффициентами разложения. Линейная комбинация с нулевыми коэффициентами называется тривиальной.

Если столбцы имеют вид

,

то матричному равенству соответствуют поэлементные равенства

Аналогично формулируется определение линейной комбинации строк.

Набор столбцов одинаковых размеров называется системой столбцов.

Система из столбцов называется линейно зависимой, если существуют такие числа , не все равные нулю одновременно, что . (3.2)

Здесь ‘о’ обозначается нулевой столбец соответствующих размеров.

Система из столбцов называется линейно независимой, если равенство (3.2) возможно только при , т.е. когда линейная комбинация в левой части тривиальная.

Любая часть системы столбцов называется подсистемой.

Пример. Используя определение, установить линейную зависимость или линейную независимость систем столбцов:

Решение. 1) Столбцы линейно зависимы, так как можно составить нетривиальную линейную комбинацию, например, с коэффициентами которая равна нулевому столбцу: .

Столбцы линейно независимы, так как равенство равносильное системе оказывается верным только при .

Свойства линейно зависимых и линейно независимых столбцов матриц.

Понятия линейной зависимости и линейной независимости определяются для строк и столбцов одинаково. Поэтому свойства, связанные с этими понятиями, сформулированные для столбцов, разумеется, справедливы и для строк.

1. Если в систему столбцов входит нулевой столбец, то она линейно зависима.

2. Если в системе столбцов имеется два равных столбца, то она линейно зависима.

3. Если в системе столбцов имеется два пропорциональных столбца , то она линейно зависима.

4. Система из столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных.

5. Любые столбцы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система столбцов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система столбцов — линейно независима, а после присоединения к ней столбца оказывается линейно зависимой, то столбец можно разложить по столбцам , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

22)

БАЗИС. КООРДИНАТЫ СТРОКИ В БАЗИСЕ.

Ба́зис — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.

Любой декартовой системе координат на плоскости или в трехмерном пространстве может быть сопоставлен базис, состоящий из векторов, каждый из которых направлен вдоль своей координатной оси. Это относится и к прямоугольным декартовым координатам (тогда соответствующий базис называется ортогональным), так и к косоугольным декартовым координатам (которым будет соответствовать неортогональный базис).

Часто удобно выбрать длину каждого из базисных векторов единичной, такой базис называется нормированным.

Наиболее часто базис выбирают ортогональным и нормированным одновременно, тогда он называется ортонормированным.

В любом векторном пространстве базис можно выбрать различным образом (поменяв направления его векторов или их длины, например).

Представление какого-то конкретного или любого вектора пространства в виде линейной комбинации векторов базиса , например:

или .

Числовые коэффициенты (a_x, a_y, a_z) называются коэффициентами разложения, а их набор в целом — представлением вектора в базисе Разложение вектора по конкретному базису единственно; разложение одного и того же вектора по разным базисам — разное, то есть получается разный набор конкретных чисел, однако в результате при суммировании — как показано выше — дают один и тот же вектор.

.

23)

Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Ранг матрицы — Размерность образа dim(im(A)) линейного оператора, которому соответствует матрица.

Обычно ранг матрицы A обозначается   ( ) или  . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.

Определение

Пусть   — прямоугольная матрица.

Тогда по определению рангом матрицы A является:

• ноль, если A — нулевая матрица;

• число 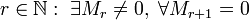 , где M_r — минор матрицы A порядка r, а M_{r + 1} — окаймляющий к нему минор порядка (r + 1), если они существуют.

Теорема (о корректности определения рангов). Пусть все миноры матрицы   порядка k равны нулю (M_k = 0). Тогда  , если они существуют.

Определение 4.1.

Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы.

Замечание. Таким образом, каждый элемент матрицы является ее минором 1-го порядка.

Определение 4.2. Ранг матрицы — это порядок ее наибольшего ненулевого минора.

Обозначения: r(A), R(A), Rang A.

Замечание. Очевидно, что значение ранга матрицы не может превышать меньшей из ее размерностей.

Примеры:

1.  , r(A)=0.

2. . Матрица В содержит единственный ненулевой элемент -  являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.

3. . Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)<3.

Для того, чтобы доказать, что r(C)=2, достаточно указать хотя бы один минор 2-го порядка, не равный 0, например, Значит, r(C)=2.

4. следовательно, r(E)=3.

Замечание. Для матриц большой размерности непосредственное вычисление всех миноров затруднительно. Поэтому в этом случае можно преобразовать матрицу к так называемому треугольному виду (когда элементы, стоящие ниже равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:

1)      транспонирование

2)      умножение строки на ненулевое число

3)      перестановка строк

4)      прибавление к элементам данной строки элементов любой другой строки, умноженных на ненулевое число

5)      вычеркивание нулевой строки.

Действительно, любая из этих операций переводит нулевые миноры в нулевые, а ненулевые — в ненулевые. Матрица, полученная в результате, не равна исходной, но имеет тот же ранг.

Пример. Найдем ранг матрицы  . Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей — разность третьей и удвоенной первой:

 .

Затем из третьей строки вычтем вторую, а к четвертой прибавим вторую:

.

После вычеркивания нулевых строк получим матрицу размерности  для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2:

.

Ее минор  следовательно,

Теорема о ранге.

Определение 4.3. Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.

Определение 4.4. Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).

В противном случае строки (столбцы) называются линейно независимыми.

Замечание. Можно доказать, что необходимым и достаточным условием линейной зависимости строк матрицы является то, что одна из них является линейной комбинацией остальных.

Теорема 4.1.

 Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов).

Доказательство (для строк).

1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.

2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0.

Докажем это свойство для строки, не входящей в базисный минор.

Добавим к базисному минору эту строку (пусть ее номер — k) и любой столбец матрицы (пусть его номер — j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:

 Поскольку является базисным минором,  поэтому, разделив полученное равенство на , найдем, что

 для всех j=1,2,…,n, где . Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.

24)

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Определение

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу  ,  ;

• прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

В некоторых курсах линейной алгебры перестановка местами двух строк матрицы не вносятся в определение элементарных преобразований так как перестановку местами любых двух строк матрицы можно получить используя умножение любой строки матрицы на константу  ,   и прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение   указывает на то, что матрица   может быть получена из   путём элементарных преобразований (или наоборот).

Вычисление ранга матрицы.

Рассмотрим матрицу типа [nm]:

Если в этой матрице выделить произвольно k столбцов и k строк, то элементы, стоящие на пересечении выделенных столбцов и строк, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдётся, по крайней мере, один минор, порядок которого будет наибольшим.

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы.

Если все элементы матрицы А равны нулю, то говорят, что ранг матрицы А равен нулю. Если ранг матрицы А равен r, то это означает, что в матрице А имеется, по крайней мере, один, отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(А).

Очевидно, что всегда выполняется соотношение

0  r  min(m,n).

Свойство 1. При транспонировании матрицы её ранг не меняется.

Свойство 2. Ранг матрицы не меняется при перестановке её столбцов (строк).

Свойство 3. Ранг матрицы не меняется при умножении всех элементов её столбца (строки) на отличное от нуля число.

Свойство 4. Ранг матрицы не изменится, если к одному из её столбцов (строк) прибавить другой столбец (строку), умножив его (её) на некоторое число.

Свойство 5. Ранг матрицы не изменится, если удалить из неё столбец (строку), состоящий из одних нулей.

Свойство 6. Ранг матрицы не изменится, если удалить из неё столбец (строку), являющийся линейной комбинацией других столбцов (строк).

Элементарными называются следующие преобразования матриц:

перестановка двух любых столбцов (строк);

умножение столбца (строки) на отличное от нуля число;

прибавление к одному столбцу (строке) линейной комбинации других столбцов (строк).

Из перечисленных выше свойств ранга матрицы следует, что при элементарных преобразованиях матрицы её ранг не меняется.

Две матрицы называют эквивалентными, если одна из них получается из другой с помощью применения конечного множества элементарных преобразований. Эквивалентные матрицы не являются равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: АВ.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например:

При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической.

Ранг канонической матрицы равен числу единиц на её главной диагонали.

На практике для вычисления ранга матрицы достаточно привести матрицу к ступенчатому виду.

Пусть нам дана матрица А, имеющая следующий вид:

Чтобы вычислить ранг матрицы А, необходимо с помощью элементарных преобразований, преобразовать её к такому виду, в котором все элементы, располагающиеся ниже главной диагонали, были равны нулю. Для этого произведём анализ строк матрицы А. Интерес вызывает 2-я строка, в которой 1-й элементы равен 1, следовательно, используя свойства 1-4, во всех строках, кроме этой, получить ряд нулевых элементов с помощью следующих преобразований над строками:

к элементам 1-ой строки прибавим элементы 2-ой, умноженные на (-2);

к элементам 3-ей строки прибавим элементы 2-ой, умноженные на (-2);

к элементам 4-ой строки прибавим элементы 2-ой, умноженные на (-3).

В результате получим матрицу ĀА:

где вторая строка матрицы А становится первой строкой в матрице Ā.

25)

a11x1+a12x2+…+a1nxn=b1, где a1n называются коэффициентами при неизвестных, а b- свободным коэффициентом. Два линейных ур-я называются равносильными, если есть общее решения. Система уравнений называется совместной, если она имеет хотя бы одно решение. Система ур-ий называется определённой, если она имеет одно единственное решение, и неопределённой, если решений множество. Матрица, эл-тами которой являются коэффициенты при неизвестных системы, называется матрицей системы. Матрица системы, дополненная столбцом свободных коэффициентов, называется расширенной матрицей.

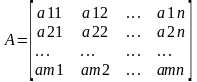
- матричная запись системы.

Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.RgA = RgA^*.Очевидно, что система (1) может быть записана в виде:x₁ + x₂ + … + x_n Доказательство.1) Если решение существует, то столбец свободных членов есть линейная комбинация толбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА^* не изменяют ранга.2) Если RgA = RgA^*, то это означает, что они имеют один и тот же Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная вышеПример. Определить совместность системы линейных уравнений:

A = ~ . RgA = 2.A* = 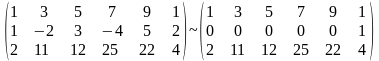RgA* = 3.Система несовместна.Пример. Определить совместность системы линейных уравнений. А = ; = 2 +

+12 = 14  0; RgA = 2;A* = RgA* = 2.Система совместна. Решения: x₁ = 1; x₂ =1/2.

Теорема 4.2 (теорема Кронекера-Капелли). Система (2.2) совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.

Доказательство.

1)      Необходимость: пусть система (2.2) совместна и ее решение. Тогда

, (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть

2)      Достаточность: если то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации  то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.

26)

Линейное пространство в линейной алгебре, да и не только в линейной алгебре, определяется следующим образом:

Множество А называется линейным векторным аффинным пространством, если

• Каждым двум элементам множества А соответствует некоторый третий элемент, называемый их суммой и принадлежащий множеству А.

• Для каждого элемента множества А и каждого числа из заданного числового множества существует элемент множества А, называемый произведением вектора на число.

Эти операции удовлетворяют следующим условиям:

• x+y=y+x коммутативность

• (x+y)+z=x+(y+z)   ассоциативность

• существует элемент 0 такой, что x+0=x

• для каждого x существует элемент -x, такой что x+(-x)=0

• 1*x=x

• a*(b*x)=(a*b)*x

• (a+b)x=ax+bx

• a(x+y)=ax+ay

Центральным понятием в линейной алгебре является понятие размерности линейного пространства,для которого используется определение линейной независимости векторов.

Система векторов линейного пространства называется линейно независимой если любая ее линейная комбинация, равная нулю имеет все коэффициенты нулевые.

Если найдется хотя бы одна линейная комбинация с отличными от нуля коэффициентами, равная нулю, то система векторов линейного пространства линейно зависима.

Существуют линейные пространства, имеющие линейно независимые системы векторов, состоящие из сколь угодно большого числа элементов. Такие пространства называются бесконечномерными.

Наоборот существуют пространства, в которых нет линейно независимых систем векторов, состоящих из сколь угодно  большого числа элементов. Такие пространства называются конечномерными.

Можно показать, что в конечномерных пространствах все системы векторов состоящие из n+1 элементов и более линейно зависимы, но тем не менее существуют линейно независимые системы векторов, состоящие из n элементов. В таком случае число n называется размерностью линейного пространства.

Любая совокупность векторов, состоящая из n элементов векторного пространства называется базисом пространства.