Собственные значения

Собственные значения линейного преобразования или оператора А, числа l,длякоторых существует ненулевой вектор х такой, что Ах = lх; вектор х называется собственным вектором. Так, С. з. дифференциального оператора L (y) с заданными краевыми условиями служат такие числа l, при которых уравнение L (y) = lу имеет ненулевое решение, удовлетворяющее этим краевым условиям. Например, если оператор L (y) имеет вид у’’, то его С. з. при краевых условиях y (0) = у (p) = 0 служат числа вида l_n = n²,где n — натуральное число, т.к. уравнению — у’’ = n²у с указанными краевыми условиями удовлетворяют функции у_п = sin nx; если же l_n¹ n² ни при каком натуральном n, то уравнению —у’’ = lу при тех же краевых условиях удовлетворяет только функция у (х) º 0. К изучению С. з. линейных операторов приводят многие задачи математики, механики и физики (аналитической геометрии и алгебры, теории колебаний, квантовой механики и т.д.).

С. з. матрицы    (i, k = 1, 2,..., n) называют С. з. соответствующего ей линейного преобразования п-мерного комплексного пространства. Их можно определить также как корни определителя матрицы А — lЕ (где Е — единичная матрица), т. е. корни уравнения

 , (*)

называемого характеристическим уравнением матрицы. Эти числа совпадают для подобных матриц А и В^–1 AB (где В — неособенная матрица) и характеризуют поэтому свойства линейного преобразования, не зависящие от выбора системы координат. Каждому корню l_i; уравнения (*) отвечает вектор x_i ¹ 0 (собственный вектор) такой, что Ax_i = l_ix_i. Если все С. з. различны, то множество собственных векторов можно выбрать за базис векторного пространства.В этом базисе линейное преобразование описывается диагональной матрицей

 .

Каждую матрицу А с различными С. з. можно представить в виде С^–1LС. Если А — самосопряжённая матрица, то её С. з. действительны, собственные векторы ортогональны, а матрицу С можно выбрать унитарной (см. Унитарная матрица). Модуль каждого С. з. унитарной матрицы равен 1. Сумма С. з. матрицы равна сумме её диагональных элементов, т. е. следу её матрицы. Знание С. з. матрицы играет важную роль в исследовании сходимости некоторых приближённых методов решения систем линейных уравнений. См. также Собственные функции.

33)

Линейные преобразования с простым спектром.

 Во многих случаях оказывается необходимым знать, может ли данное линейное преобразование j иметь в некоторой базе диагональную матрицу. Приведем достаточное условие того, что линейное преобразование может быть задано диагональной матрицей.

Докажем сначала следующие вспомогательные результаты:

Линейное преобразование j тогда и только тогда задается в базе е₁, е₂, ..., е_n диагональной матрицей, если все векторы. этой базы являются собственными векторами преобразования j.

Действительно, равенство

e_ij=l_i e_i

равносильно тому, что в i-й строке матрицы, задающей преобразование j в указанной базе, равны нулю все элементы, стоящие вне главной диагонали, а на главной диагонали (т. е. на i-м месте) стоит число l_i.

Собственные векторы b₁, b₂,…, b_k, линейного преобразования j, относящиеся к различным собственным значениям, составляют линейно независимую систему,

Будем доказывать это утверждение индукцией по k, так как при k =1 оно справедливо - один собственный вектор, будучи отличным от нуля, составляет линейно независимую систему. Пусть

b_ij=l_i b_i     i = 1, 2,…, k,

и

l_i ¹ l_j при i ¹ j.

Если существует линейная зависимость

a₁b₁+a₂b₂+…+a_kb_k = 0                                       (9)

где, например. a₁¹0, то, применяя к обеим частям равенства (9) преобразование j, получим

a₁l₁ b₁+a₂l₂b₂+…+a_kl_kb_k = 0

Вычитая отсюда равенство (9), умноженное на l_k, получаем

a₁(l₁-l_k) b₁+a₂(l₂-l_k)b₂+…+a_k-1(l_k-1-l_k)b_k-1 = 0

что дает нетривиальную линейную зависимость между векторами b₁, b₂,…, b_k-1, так как a₁(l₁-l_k)¹0.

Говорят, что линейное преобразование j действительного линейного пространства V_n имеет простой спектр, если все его характеристические корни действительны и различны. Преобразование. j имеет, следовательно, n различных собственных значений, а по­этому, по доказанной теореме, в пространстве V_n существует база, составленная из собственных векторов этого преобразования. Таким образом, всякое линейное преобразование с простыми спектром может быть задано диагональной матрицей.

Переходя от линейного преобразования к матрицам, его задающим, мы получаем следующий результат:

Всякая матрица, все характеристические корни которой действительны и различны, подобна диагональной матрице или, как говорят, такая матрица приводится к диагональному виду.

34)

Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно n-мерное евклидово пространство обозначается  , хотя часто используется не вполне приемлемое обозначение  .

1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство   с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

,

в простейшем случае (евклидова норма):

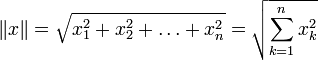
где   (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

2. Метрическое пространство, соответствующее пространству описанному выше. То есть   с метрикой, введённой по формуле:

,

где   и  .

Вектор. Ортонормированный базис. Если векторы e _{1 ,} e ₂ , e ₃ попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x ₁, x ₂, x ₃ - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.

Будем предполагать, что в пространстве R ³ выбрана правая система декартовых прямоугольных координат {0, i, j, k }.

Вектор. Векторное произведение. Векторным произведением вектора а на вектор b называется вектор c, который определяется следующими тремя условиями:

1. Длина вектора c численно равна площади параллелограмма, построенного на векторах a и b, т. е. ê c ê = ê a ê b ê sin ( a ^ b ).

2. Вектор c перпендикулярен к каждому из векторов a и b.

3. Векторы a, b и c, взятые в указанном порядке, образуют правую тройку.

Для векторного произведения c вводится обозначение c = [ ab ] или  c = a b.

Если векторы a и b коллинеарны, то sin( a^b ) = 0 и [ ab ] = 0, в частности, [ aa ] = 0. Векторные произведения ортов: [ ij ] = k, [ jk ] = i, [ ki ] = j.

Если векторы a и b заданы в базисе i, j, k координатами a (a ₁, a ₂, a ₃ ), b (b ₁, b ₂, b ₃ ), то

(неопределённость  ). Пусть функции f (х) и g (х): 1. непрерывны на полуинтервале (a, b]; 2. ,  ; 3. существуют производные f '(х) и g'(х) на интервале (a,b), причём g'(х)  0; 4. существует (конечный или бесконечный)  . Тогда существует , и  .

Теорема остаётся справедливой и для случаев  . В целом теоремы Лопиталя - это мощное средство для раскрытия неопределённостей всех видов.

Соответствия. Функции и отображения. Операции. Перестановки, размещения и сочетания. Упорядоченные и неупорядоченные разбиения множества. Инверсии и обратные перестановки. Перманенты и их применения. Алгоритмы генерации комбинаторных объектов. 

35)