12. Волны в упругой среде

Уравнение плоской волны

ξ(х,t) = A cosω(t − x/v), или ξ(х, t) = Acos(ωt −kx),

где ξ(х,t) − смещение точек среды с координатой х в момент времени t; ω−

угловая частота; v − скорость распространения колебаний в среде (фазовая

скорость); k − волновое число; k =2π/λ; λ − длина волны.

Длина волны связана с периодом Т колебаний и частотой v соотношениями

λ = vT и λ = v/v.

Разность фаз колебаний двух точек среды, расстояние между которыми (раз-

ность хода) равно Δх,

Δφ = (2π/λ) Δx,

где λ − длина волны.

35

Уравнение стоячей волны

ξ(х,t) = Acosω(x/v)∙cosωt, или ξ(x,t) = Acoskx∙cosωt.

Фазовая скорость продольных волн в упругой среде:

в твердых телах v = √Е/ρ, где Е − модуль Юнга; ρ − плотность веще-

ства;

в газах v = √γRT/M, или v = √γp/ρ, где γ − показатель адиабаты ( γ =

= ср/cv − отношение удельных теплоёмкостей газа при постоянных дав-

лении и объёме); R − молярная газовая постоянная; T − термодинами-

ческая температура; M − молярная масса; p − давление газа.

Амплитуда звукового давления

ро = 2πvρvA,

где v − частота звука; A − амплитуда колебаний частиц среды; v − скорость

звука в среде; ρ − её плотность.

Средняя объёмная плотность энергии звукового поля

‹ w › = ρ(dξо/dt)²/2 = po²/(2ρv²) = ρω²A²,

где dξo/dt − амплитуда скорости частиц среды; ω − угловая частота звуковых

волн.

Энергия звукового поля, заключенного в некотором объёме V,

W = ‹ w ›V.

Поток звуковой энергии

Ф = W/t,

где W − энергия, переносимая через данную поверхность за время t.

Интенсивность звука (плотность потока звуковой энергии)

I = Ф/S.

Интенсивность звука связана со средней объёмной плотностью энергии зву-

кового поля соотношением

I = ‹ w ›v,

где v − скорость звука в среде.

Связь мощности N точечного изотропного источника звука с интнсивностью

звука

I = N/(4πr²),

где r − расстояние от источника звука до точки звукового поля, в которой оп-

ределяется интенсивность.

Удельное акустическое сопротивление среды

Zs = ρv. 36

Акустическое сопротивление

Za = Z/S,

где S − площадь сечения участка акустического поля ( например, площадь по-

перечного сечения трубы при распространении в ней звука).

Уровень интенсивности звука (уровень звуковой мощности)(дБ)

Lp = 10 lg(I/Io),

где Io − условная интенсивность, соответствующая нулевому уровню интен-

сивности (Io = 1 пВт/м²).

ВОПРОСЫ И УПРАЖНЕНИЯ

1. Какое движение называется: а) колебательным; б) периодическим; в) гармони-

ческим?

2.Дайте определение амплитуды и фазы гармонических колебаний.

3. Что такое частота колебаний?

4. Какой физический смысл циклической частоты колебания?

5. Чему равно изменеиие фазы колебания за время, равное периоду колебаний?

6. Дайте определение свободного колебания. Как, зная начальные условия

х(0) = хо и v(0)= vо, определить амплитуду и начальную фазу колебаний.

7. При каких условиях свободные колебания математического и физического ма-

ятника можно считать гармоническими?

8. При каких условиях колебания пружинного маятника можно считать гармони-

ческими?

9. Что означает требование малости амплитуды (по сравнению с чем?) и к каким

колебательным системам оно относится?

10. Что такое приведенная длина физического маятника, свойство обратимости и

центр качаний?

11. Почему в формулу полной энергии гармонических колебаний не входит время

в отличие от формул кинетической и потенциальной энергии?

12. Как определить, что записывать в уравнении гармонических колебаний – за-

кон синуса или косинуса? В каких случаях это имеет значение ?

13. Каков период изменения кинетической(и потенциальной) энергии гармоничес-

кого осциллятора? Показать расчетами.

13. В чем сущность метода векторных диаграмм сложения колебаний? Отражени-

ем какого, более общего метода представления колебаний, является, этот метод?

13. Что такое фигуры Лиссажу? Как и какие параметры складывемых колебаний

можно по ним определить? Сформулируйте условие наблюдения стабильной фигу-

ры Лиссажу.

16. Дайте определение логарифмического декремента затухания.

17. Что такое апериодический процесс? Сформулирйте условие возникновения

аперодичности.

18. Каков физический смысл добротности механической колебательной системы?

19. Проследите цепь превращений энергии в процессе затухающтх колебаний.

20. Установите связь относительной потери энергии Е / E c добротностью Q.

21. Получите выражение для резонансной частоты. Запишите условие исчезнове-

ния резонанса при увеличении затухания. 37

22.Получите выражение для частоты биений в случае связанных колебаний двух

физических маятников.

23. Какие колебания называются нормальными? Получите нормальные частоты в

случае связанных колебаний двух физических маятников.

24. Какое движение называется волновым?

25. Что такое поперечные и продольные волны? Приведите примеры. Почему в

жидких и газообразных средах могут существовать только продольные волны?

26. Выведите уравнение плоской бегущей монохроматической волны.

27. Каков физический смысл знака в уравнеии волны перед kx?

28. Каков физический смысл волнового числа k?

29. Каков физический смысл фазовой скорости?

30. Что такое когерентные колебания и когерентные волны?

31. Возникновение интерференции волн. При каких условиях образуются стоячие

волны? Почему они так называются, что такое узлы и пучности стоячей волны?

32. Сформулируйте условие наблюдения максимального звучания у открытого

конца U-образной трубы, заполненной жидкостью.

33. Какими величинами определяется скорость продольных и поперечных волн?

34. Получите волновое уравнение для случая плоской монохроматической волны.

35. Запишите выражения для кинетической и потенциальной энергии бегущей

волны.

36. Что собой представляет поток плотности энергии, связанной с бегущей вол-

ной?

37. Получите формулу для вектора Умова-Пойтинга.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Точка совершает колебания по закону х(t) = Аcos(ωt + φ), где

А = 2 см. Определить начальную фазу φ, если х(0) = −√3 см и dx/dt(0) < 0.

Построить векторную диаграмму для момента t = 0.

Да н о:

A = 2 cм,

х(0) = −√3 см,

dx/dt(0) < 0.

О п р е д е л и т ь : φ = ?; построить векторную диаграмму.

Р е ш е н и е. Воспользуемся уравнением движения и выразим смещение в

момент t = 0 через начальную фазу φ: x(0) = Acos φ. Отсюда найдем началь-

ную фазу:

φ = arcos[x(0)/A].

Подставим в это выражение заданныезначения х(0) и А: φ = arcos(−√3/2).

Значению аргумента (−√3/2) удовлетворяют два значения угла:

φ1 = 5π/6 и φ2 = 7π /6.

Для того чтобы решить, какое из этих значений угла φ удовлетворяет ещё

и условию dx/dt(0) < 0, найдем сначала dx/dt(t):

dx/dt (t) = −ωA sin(ωt + φ).

Подставив в это выражение значение t =0 и поочерёдно значения началь-

ных фаз φ1 = 5π/6 и φ2 = 7π/6, найдем

dx1/dt(0) = − 1/2 Aω и dx2/dt(0) = ½ Aω. 38

Так как всегда А > 0 и ω > 0, то условию dx/dt(0) < 0 удовлетворяет толь-

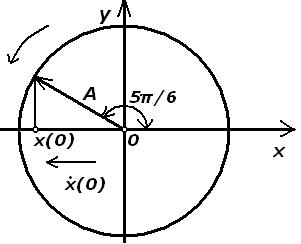
Рис. 29

ко первое значение начальной фазы. Таким образом, искомая начальная фа-

за φ = 5π/6.

По найденному значению φ построим векторную диаграмму (рис. 29).

Ответ: φ = 5π/6; векторная диаграмма представлена на рис. 29.

Пример 2. Материальная точка массой m = 5 г совершает гармоничес-

кие колебания с частотой v = 0.5 Гц. Амплитуда колебаний А = 3 см. Опре-

делить: 1) cкорость v в момент времени, когда смещение х = 1.5 см; 2) мак-

симальную силу Fmax, действующую на точку; 3) полную энергию Е колеб-

лющейся точки.

Д а н о:

m = 5 г = 0.005 кг,

v = 0.5 гц,

А = 3 см = 0.03 м,

х(t) = 1.5 см = 0.015 м.

О п р е д е л и т ь: 1) v(t) =? 2) Fmax = ? 3) E = ?

Р е ш е н и е. 1. Уравнение гармонического колебания имеет вид

х(t) = А cos (ωt + φ) (1)

а формулу скорости получим, взяв первую производную по времени от сме-

щения:

v = dx/dt = − Aω sin (ωt + φ). (2)

Чтобы выразить скорость через смещение, надо исключить из формул (1) и

(2) время. Для этого возведем оба уравнения в квадрат, разделив первое на А²,

второе на А²ω² и сложим:

х²/A² + v²/(A²ω²) = 1, или х²/A² + v²/(4πv²A²) = 1.

Решив последнее уравнение относительно v, найдём

v = ± 2πv√ A² − x².

Выполнив вычисления по этой формуле, получим

v = ± 8,2 см/c.

Знак плюс соответствует случаю, когда направление скорости совпадает с

положительным направлением оси х, знак минус, − когда направление

скорости совпадает с отрицательным направлением оси х.

Смещение при гармоническом колебании кроме уравнения (1) может быть 39

определено также уравнением

х(t) = A sin(ωt + φ).

Повторив с этим уравнением такое же решение, получим тот же ответ.

2. Силу, действующую на точку, найдем по второму закону Ньютона:

F = ma, (3)

где а − ускорение точки, которое получим, взяв производную по времени от

скорости:

a = dv/dt = − Aω² cos(ωt + φ), или а = − 4π²v² A cos(ωt +φ).

Подставив выражение ускорения в формулу (3), получим

F = − 4π²v²mA cos (ωt + φ).

Отсюда максимальное значение силы

Fmax = 4π²v²mA.

Подставив в это уравнение значения величин π, v, m и А, найдем

Fmax = 1.49 мН.

3. Полная энергия колеблющейся точки равна сумме кинетической и потен-

циальной энергий, вычисленных для любого момента времени. Проще всего вы-

числить полную энергию в момент, когда кинетическая энергия достигает макси-

мального значения. В этот момент потенциальная энергия равна нулю. Поэтому

полная энергия Е колеблющейся точки равна максимальной кинетической энер-

гии Emax:

Е = Еmax = 1/2 mv²max. (4)

Максимальную скорость определим из формулы (2), положив cos(ωt + φ) = 1:

vmax = 2πvA. Подставив выражение скорости в формулу (4), найдем

Е = 2π²mv²A².

Подставив значения величин в эту формулу и произведя вычисления, получим

Е = 2·(3.14)²·5·10ˉ³·(0.5)²·(3·10ˉ²)² Дж = 22.1·10ˉ²*³ Дж, или Е = 22.1 мкДж.

Ответ: 1) v = ± 8.2 см/c; 2) Fmax = 1.49 мН; 3) E = 22.1 мкДж.

Пример 3. На концах тонкого стержня длиной l = 1 м и массой m3 = 400 г ук-

пленны шарики малых пазмеров массами m1 = 200 г и m2 = 300 г. Стержень

колеблется около горизонтальной оси, перпендикулярной стержню и проходящей

через его середину ( точка О на рис. 30). Определить период Т колебаний,

cовершаемых стержнем.

Д а н о: l = 1 м,

m1 = 200 г,

m2 = 300 г,

m3 = 400 г,

Т = ?

Рис. 30 40

Р е ш е н и е: Период колебаний физического маятника, каким является стер-

жень с шариками, определяется соотношением

Т = 2π√Io/(mglc) , (1)

где Io − момент инерции маятника относительно оси колебаний; m − его масса;

lc − расстояние от центра масс маятника до оси.

Момент инерции данного маятника равен сумме моментов инерции шариков

Io1 и Io2 и стержня Io3:

Io = Io1 + Io2 + Io3. (2)

Принимая шарики за материальные точки, выразим их моменты нерции:

Io1 = m1(l/2)²; Io2 = m2(l/2)². Так как ось проходит через середину стержня, то его

момент инерции относительно этой оси Io3 = 1/12 m3l². Подставив полученные

выражения Io1, Io2 и Io3 в формулу (2), найдем общий момент инерции физи-

ческого маятника:

Io = m1(l/2)² + m2(l/2)² + 1/12 m3l² = 1/12l²(3m1 + 3m2 + m3).

Произведя вычисления по этой формуле, найдем

Io = 0.158 кг·м².

Масса маятника состоит из масс шариков и массы стержня:

m = m1 + m2 + m3 = 0.9 кг.

Рассояние lc центра масс маятника от оси колебаний найдем из следу-

ющих соображений. Если ось х направить вдоль стержня и начало координат

совместить с точкой О, то искомое расстояние lc равно координате центра

масс маятника, т.е.

lc = xc = ∑mixi /∑mi = [m1(− l/2) + m2(l/2) + m3·0]/(m1 + m2 + m3), или

lc = [(m2 − m1)l]/[2(m1 + m2 + m3)] = (m2 − m1)l/2m.

Подставив значения величин m1, m2, m, l и произведя вычисления, найдём

lc = 5.55 см.

Произведя расчёты по формуле (1), получим период колебаний физическо-

го маятника:

T = 2·3.14√0.158/(0.9·9.81·5.55·10ˉ) c = 11.2 c.

Ответ: T = 11.2 c.

Пример 4. Физический маятник представляет собой тонкий однородный

стержень. Определить длину стержня, если частота колебаний маятника макси-

мальна, когда точка подвеса О находится от центра масс С на расстоянии 20.2

см (рис. 31). 41

Рис. 31

Д а н о: х = 20.2 см = 0.202 м, ω = ωmax.

О п р е д е л и т ь l.

Р е ш е н и е. Циклическая частота колебаний физического маятника

ω = √ mgx/Ic, (1)

где m − масса маятника; Io − момент инерции его относителтно оси колебаний.

Согласно теореме Штейнера, момент инерции стержня относительно точки

подвеса, отстоящей от центра масс на расстоянии х

Io = ml²/12 + mx². (2)

Подставив (2) в (1), получим

ω = √ 12gl/(l² + 12x²) . (3)

Найдем экстремум функции (3):

dω/dx = 6g(l² − 12x²)/[x¹/ ²(l² + 12x²)³/²] = 0,

откуда

l² − 12x² = 0,

т.е. искомая длина маятника

l =2√3 x.

Вычисляя, получим l = 70 см.

Ответ: l = 70 см

Пример 5. Физический маятник представляет собой стержень длиной l= 1м

и массой 3m1 c прикрепленным к одному из его концов обручем диаметром d =

= 1/2 l и массой m1. Горизонтальная ось Оz маятника проходит через середину

стержня перпендикулярно ему (рис.32). Определить период Т колебаний тако-

го маятника.

Рис.32 42

Д а н о:

l = 1 м,

3m1 − масса стержня,

m1 − масса обруча,

d =1/2 l ( d − диаметр обруча),

T = ?

Р е ш е н и е: Период колебаний физического маятника определяется по

формуле

Т = 2π√Io/(mglc), (1)

где Io − момент инерции маятника относительно оси колебаний; m − его мас-

са; lc − расстояние от центра масс маятника до оси колебаний.

Момент инерции маятника равен сумме моментов инерции стержня Io1 и

обруча Io2:

Io = Io1 + Io2. (2)

Момент инерции стержня относительно оси, перпендикулярной стержню и

проходящей через его центр масс, определяется по формуле Io1 = 1/12 ml². В

данном случае m = 3m1 и

Io1 = 1/4 m1l².

Момент инерции обруча найдём, воспользовавшись теоремой Штейнера

Io = Ic + ma², где Io − момент инерции относительно произвольной оси; Ic −

момент инерции относительно оси, проходящей через центр масс параллельно

заданной оси; а − расстояние между указанными осями. Применив эту формулу

к обручу, получим

Io2 = m1 (l/4)² + m1(3l/4)² = 5/8 m1l².

Подставив выражения Io1 и Io2 в формулу (2), найдем момент инерции ма-

ятника относительно оси вращения:

Io = 1/4m1l² + 5/8m1l² = 7/8 m1l².

Расстояние lc от оси маятника до его центра масс равно

lc = ∑mixi /∑mi = [3m1·0 + m1·(3l/4)] = ( 3/4m1l)/ 4m1, или

lc = 3/16 l.

Подставив в формулу (1) выражения Io, lc и массы маятника (m = 3m1 +

+ m1 = 4m1), найдём период его колебаний:

T = 2π√(7/8m1l²)/(4m1g·3/16l) = 2π√7l/6g.

После вычисления по этой формуле получим

Т = 2.17 с.

Ответ: T = 2.17 c.

Пример 6. Складываются два колебания одинакового направления, выража-

43

емых уравнениями х1 = A1 cosω(t + τ1); x2 = A2 cosω(t + τ2), где А1 = 1 см, А2 =

= 2 см, τ1 = 1/6 c, τ2 = 1/2 c, ω = π cˉ¹. 1. Определить начальные фазы φ1 и φ2

составляющих колебаний. 2. Найти амплитуду А и начальную фазу φ резуль-

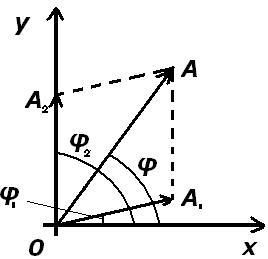тирующего колебания.

Д а н о:

A1 = 1 см = 0.01 м,

А2 = 2 см = 0.02 м,

τ1 = 1/6 c,

τ2 = 1/2 c,

ω = π cˉ¹

A = ? Рис.33

φ = ?

Р е ш е н и е . 1. Уравнение гармонического колебания имеет вид

х = А cos(ωt + φ). (1)

Преобразуем уравнеия, заданные в условии задачи, к виду:

х1 = А1 cos(ωt + ωτ1), x2 = A2 cos(ωt + ωτ2). (2)

Из сравнения выражений (2) с равенством (1) находим начальные фазы первого

и второго колебаний:

φ1 = ωτ1 = π/6 рад и φ2 = ωτ2 = π/2 рад.

2. Для определения амплитуды А результирующего колебания удобно вос-

пользоваться векторной диаграммой, представленной на рис. 33. Согласно теоре-

ме косинусов, получим

А =√ А1² + А2² + 2А1А2 cos∆φ , (3)

где ∆φ − разность фаз составляющих колебаний. Так как ∆φ = φ2 − φ1, то, под-

ставляя найденные значения φ2 и φ1, получим ∆φ = π /3 рад.

Подставим значения А1, А2 и ∆φ в формулу (3) и произведём вычисления:

А = 2.65 см.

Тангенс начальной фазы φ результирующего колебания определим непос-

редственно из рис. 33: tg φ = (A1 sinφ1 + A2 sinφ2)/(A1 cosφ1 + A2 cosφ2), откуда на-

чальная фаза

φ = arctg[(A1 sinφ1 + A2 sinφ2)/(A1 cosφ1 + A2 cosφ2)].

Подставим значения А1, А2, φ1, φ2 и произведём вычисления:

φ = arctg(5/√ 3) = 70.9º = 0.394π рад.

Так как угловые частоты складываемых колебаний одинаковы, то результи-

рующее колебание будет иметь ту же частоту ω. Это позволяет написать урав-

нение результирующего колебания в виде х = А cos(ωt + φ), где А = 2.65 см,

ω = π сˉ¹, φ = 0.394π рад.

Ответ: x = A cos(ωt + φ); A = 2.65 см; ω = π cˉ¹; φ = 0.394π рад.

Пример 7. Материальная точка участвует одновременно в двух взаимно

перпендикулярных гармонических колебаниях, уравнения которых 44

х = А1 cosωt, (1)

y = A2 cos(ω/2), (2)

где А1 = 1 см, А2 = 2 см, ω = π сˉ¹. Найти уравнение траектории точки. По-

строить траекторию с соблюдением масштаба и указать направление движения

точки.

Р е ш е н и е. Чтобы найти уравнение траектории точки, исключим время t

из заданных уравнений (1) и (2). Для этого воспользуемся формулой cos(α/2) =

= √ (1/2)(1 + cosα). В данном случае α =ωt, поэтому

y = A2 cos(ω/2)t = A2 √ (1/2)(1 + cosωt).

Так как согласно формуле (1) cosωt = x/A1, то уравнение траектории

y = A2√ (1/2)(1 + x/A1). (3)

Полученное выражение представляет собой уравнение параболы, ось кото-

рой совпадает с осью Ох. Из уравнений (1) и (2) следует, что смещение точки

по осям координат ограничено и заключено в пределах от −1 до +1 см по

оси Ох и от −2 до +2 см по оси Оу.

Для построения траектории найдем по уравнению (3) значения у, соответ-

ствующие ряду значений х, удовлетворяющих условию ‌‌‌‌|х| ≤ 1 см, и составим‌‌‌

таблицу:

х, см	− 1	− 0.75	− 0.5	0	+0.5	+1
у, см	0	±0.707	± 1	± 1.41	± 1.73	± 2

Начертив координатные оси и выбрав масштаб, нанесём на плоскость хОу

найденные точки. Соединив их плавной кривой, получим траекторию точки,

совершающей колебания в соответствии с уравнениями движения (1) и (2)

(рис. 34).

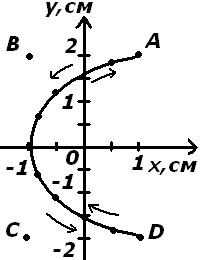
Рис.34

Для того чтобы указать направление движения точки, проследим за тем,

как изменяется её положение с течением времени. В начальный момент t = 0

координаты точки х(0) = 1 см и у(0) = 2 см. В последующий момент време-

ни, например при t1 = 1 c, координаты точек изменятся и станут равными х(1)=

= −1 см, у(1) = 0. Зная положение точек в начальный и последующий (близкий)

моменты времени, можно указать направление движения точки по траектории.

На рис. 34 это направление движения указано стрелкой ( от точки А к началу

координат). После того как в момент t2 = 2 c колеблющаяся точка достигнет

точки D, она будет двигаться в обратном направлении.

Ответ: Траектория движения является параболой и в плоскости хОу опи-

сывается уравнением у = А2√ (1/2)(1 + x/A1).

Пример 8. Логарифмический декремент затухания тела, колеблющегося с 45

частотой 50 Гц, равен 0.01. Определить: 1) время, за которое амплитуда коле-

баний тела уменьшится в 20 раз; 2) число полных колебаний тела, чтобы про-

изошло подобное уменьшение амплитуды.

Д а н о: v = 50 Гц; Θ = 0.01, A = 0.05 Ao.

О п р е д е л и т ь: 1) t; 2) N.

Р е ш е н и е. Амплитуда затухающих колеаний

−δt

А = Ао e , (1)

где Ао − амплитуда в момент t = 0; δ − коэффициент затухания.

Логарифмический декремент затухания Θ = δТ ( Т = 1/v − условный период

затухающих колебаний). Тогда δ = Θv и выражение (1) можно записать в виде

−Θvt

А = Ао е ,

откуда искомое время

t = (1/Θv) ln(Ao/A).

Число искомых полных колебаний

N = t/T = tv.

Вычисляя, получаем: 1) t = 6 c; 2) N = 300.

Ответ: 1) t = 6 c; 2) N = 300.

Пример 9. Груз массой m = 50 г, подвешенный на нити длиной l = 20 см,

cовершает колебания в жидкости. Коэффициент сопротивления r = 0.02 кг/c.

На груз действует сила F = 0.1 cosωt, H. Определить: 1) частоту вынужда-

ющей силы, при которой амплитуда вынужденных колебаний максимальна;

2) резонансную амплитуду.

Д а н о: m = 50 г = 0.05 кг, l = 20 см = 0.2 м, r =0.02 кг/c, F = 0.1 cosωt, H.

О п р е д е л и т ь: 1) ωрез; 2) Aрез.

Р е ш е н и е. Очевидно, что частота вынуждающей силы, при которой амп-

литуда вынужденных колебаний максимальна, является резонансной частотой:

ωрез = √ ωо² − 2δ² , (1)

где ωо − собственная частота колебаний системы; δ = r/(2m) − коэффициент

затухания.

Груз, подвешенный на нити, можно принять за математический маятник, то-

гда ωо = √ g/l . Подставив значения ωо и δ в формулу (1), найдём искомую

резонансную частоту:

ωрез = √ (g/l) − (r²/2m²) .

Подставив в выражение для амплитуды вынужденных колебаний

А = Fo [m√(ωo² − ω²)² + 4 δ²ω² ],

где Fo − амплитудное значение вынуждающей силы ( по условию задачи Fo=

= 0.1 H), формулу (1), найдём искомую резонансную амплитуду:

46

Aрез = Fo/ (2mδ√ωo² − δ²) = Fo/r√[(g/l) + (r²/4m²)].

Вычисляя, получим: 1) ωрез = 7 рад/c; 2) Aрез = 71.4 см.

Ответ: 1) ωрез = 7 рад/c; 2) Aрез = 71.4 см.

Пример 10. Плоская синусоидальная волна распростаняется вдоль прямой,

совпадающей с положительным направлением оси х в среде, не поглощаю-

щей энергию, со скоростью v = 15 м/c. Две точки, находящиеся на этой прямой

на расстояниях х1 = 5 м и х2 = 5.5 м от источника колебаний, колеблются с раз-

ностью фаз Δφ = π/5. Амплитуда волны А = 4 см. Определить: 1) длину вол-

ны; 2) уравнение волны; 3) смещение ξ1 первой точки в момент времени t =

= 3 c.

Д а н о: v = 15 м/c, x1 = 5 м, х2 = 5.5 м, Δφ = π/5, A = 4 см = 0.04 м, t = 3 c.

О п р е д е л и т ь: 1) λ ; 2) ξ(x, t); 3) ξ1 .

Р е ш е н и е. Разность фаз колебаний двух точек волны

Δφ = (2π/λ)Δx,

где Δ х = х2 − х1 − расстояние между этими точками.

Тогда

Λ = 2π(х2 − х1)/Δφ.

Циклическая частота ω = 2 π /T, где Т= λ/v. Следовательно, ω =2πv/λ.

Уравнение плоской синусоидальной волны, распространяющейся вдоль по-

ложительного направления оси х,

ξ(х, t) = А cosω(t − x/v) = A cos[(2π/λ)(vt − x)].

Чтобы найти смещение ξ1, надо в это уравнение подставить значения t и x1.

Вычисляя, получаем:1)λ = 5 м; 2)ξ(x, t) = 0.04cos[6πt − (2π/5)x],м 3)ξ1 = 4 см.

Ответ: 1) λ = 5 м; 2) ξ(x, t) = 0.04cos [6πt − (2π/5)x]; 3) ξ1 = 4 см.

Пример 11. Поперечная волна распространяется вдоль упругого шнура со

скоростью v = 15 м/c. Период Т колебаний точек шнура равен 1.2 с, ампли-

туда А = 2 см. Определить: 1) длину волны λ; 2) фазу φ колебаний, смеще-

ние ξ, скорость dξ/dt и ускорение d²ξ /dt² точки, отстоящей на расстоянии

х = 45 м от источника волн в момент t = 4 c; 3) разность фаз Δφ колебаний

двух точек, лежащих на луче и отстоящих от источника волн на расстояниях

х1 = 20 м и х2 = 30 м.

Д а н о: v = 15 м/c, T = 1.2 c, A = 2 см.

О п р е д е л и т ь: 1) λ; 2) φ, ξ, dξ/dt, d²ξ/dt² для х = 45 м и t = 4 c;

3) Δφ для х1 = 20 м и х2 = 30 м.

Р е ш е н и е. 1. Длина волны равна расстоянию, которое волна проходит

за один период, и может быть найдена из соотношения

λ = vT.

Подставив значения величин v и T, получим

λ = 18 м.

2. Запишем уравнение волны: 47

ξ = А cosω (t − x/v), (1)

где ξ − смещение колеблющейся точки; x − рассояние точки от источника

волн; v − скорость распространения волн.

Фаза колебаний точки с координатой х в момент времени t определя-

ется выражением, стоящим в уравнении волны под знаком косинуса:

φ = ω[ t − (x/v)], или φ = (2π/T)[t − (x/v)],

где учтено, что ω = 2π/T.

Произведя вычисления по последней формуле, получим

φ = 5.24 рад, или φ = 300°.

Смещение точки определим, подставив в уравнение (1) значения амплиту-

ды А и фазы φ:

ξ = 1 см.

Скорость dξ/dt точки находим, взяв первую производную от смещения по

времени:

dξ/dt = − Aω sin (t − x/v) = −( 2π/T) sin ω(t − x/v) = (2πA/T) sin φ.

Подставив значения величин π , А, Т и φ и произведя вычисления, по-

лучим

dξ/dt = 9 см/c.

Ускорение есть первая производная от скорости по времени или вторая про-

изводная от смещения по времени, поэтому

d²ξ/dt² = − Aω² cos ω(t − x/v) = − (4π²A/T²) cosφ.

Произведя вычисления по этой формуле, найдём

d²ξ/dt² =27.4 см/c².

3. Разность фаз Δφ колебаний двух точек связана с расстоянием Δх меж-

ду этими точками соотношением

Δφ =(2π/λ)Δx.

Подставив значения величин λ, х1 и х2 и вычислив, получим

Δφ =3.49 рад, или Δφ = 200°.

Ответ: 1) λ = 18 м; 2) φ = 5.24 рад (или φ = 300°), ξ = 1 см, dξ/dt= 9 см/c,

d²ξ/dt² = 27.4 см/c² для х = 45 м и t = 4 c; 3) Δφ = 3.49 рад ( или

Δφ = 200°) для х1 = 20 м и х2 = 30 м.

48

ЗАДАЧИ ГРУППЫ А

1.(В.12.7). Начальная фаза гармонического колебания φ= 0. Через ка-

кую долю периода скорость точки будет равна половине её максимальной ско-

рости?

Ответ: t = T/6.

2.(В.12.12). Точка совершает синусоидальное гармоническое колебание.

период колебаний Т = 2 с, амплитуда А = 50 мм, начальная фаза φ = 0.

Найти скорость v точки в момент времени, когда смещение точки от положе-

ния равновесия х = 25 мм.

Ответ: v = 13.6 cм/c.

3.(В.12.20). Полная энергия тела, совершающего синусоидальное гармо-

ническое колебание, Е = 30 мкДж; максимальная сила, действующая на тело,

Fmax = 1.5 мН. Написать кинематическое уравнение движения этого тела, если

период колебаний Т = 2 с и начальная фаза φ = π/3.

Ответ: x = 0.04 sin(πt + π/3) м.

4.(В.12.24). К пружине подвешен груз. Максимальная кинетическая энер-

гия колебаний груза Ек max = 1 Дж. Амплитуда колебаний А = 5 см. Найти

жесткость k пружины.

Ответ: k = 805 H/м.

5.(В.12.25). Как изменится период вертикальных колебаний груза, вися-

щего на двух одинаковых пружинах, если от последовательного соединения

пружин перейти к параллельному их соединению?

Ответ: уменьшится в 2 раза.

6.(В.12.26). Медный шарик, подвешенный к пружине, совершает вертикаль-

ные колебания. Как изменится период колебаний, если к пружине подвесить

вместо медного шарика алюминиевый такого же радиуса?

Ответ: уменьшится в 1.8 раза.

7.(В.3.45). Однородный стержень длиной l = 0.5 м совершает малые

колебания в вертикальной плоскости около горизонтальной оси, проходящей

через его верхний конец. Найти период колебаний Т стержня.

Ответ: T = 1.16 c.

8.(В.3.47). На концах вертикального стержня укреплены два груза. Центр

масс грузов находится ниже середины стержня на расстоянии d = 5 cм. Найти

длину l стержня, если известно, что период малых колебаний стержня с гру-

зами вокруг горизонтальной оси, проходящей через его середину, Т = 2 с.

массой стержня пренебречь по сравнению с массой грузов.

Ответ: l = (T√gd)/π = 0.446 м.

9.(В.3.48). Обруч диметром D = 56.5 см висит на гвозде, вбитом в стену,

совершает малые колебания в плоскости, параллельной стене. Найти период

колебаний Т обруча.

Ответ: T = 1.5 c.

10.(В.3.49). Какой наименьшей длины l надо взять нить, к которой под-

вешен однородный шарик диаметром D = 4 см, чтобы при определении перио-

да малых колебаний Т шарика можно было рассматривать его как математи-

ческий маятник? Ошибка δ при таком допущении не должна превышать 1 %.

Ответ: l = 0.069 м.

11.(В.3.50). Однородный шарик подвешен на нити, длина которой l рав-

на радиусу шарика R. Во сколько раз период малых колебаний Т1 этого маят-

ника больше периода колебаний Т2 математического маятника с таким же рас-

стоянием от центра масс до точки подвеса?

Ответ: T1/T2 = 1.05.

12.(В.12.30). Написать уравнение движения, получающегося в результате

сложения двух одинаково направленных гармонических колебаний с одинако-

вым периодом Т = 8 с и одинаковой амплитудой А = 0.02 м. Разность фаз меж-

ду этими колебаниями φ2 − φ1 = π/4. Рачальная фаза одного из этих колебаний

равна нулю.

Ответ: x = 3.7 sin( πt/4 + π/8) см.

13.(В.12.31). Найти амплитуду А и начальную фазу φ гармонического

колебания, полученного от сложения одинаково направленных колебаний, дан-

ных уравнениями

х1 = 0.02 sin (5πt + π/2) м и х2 = 0.03 sin (5πt + π/4).

Ответ: A = 4.6 см; φ = 62°46′.

14.(В.12.39). Точка участвует в двух взаимно перпендикулярных колебани-

ях х =2 sin ωt м и y = 2 cos ωt м. Найти траекторию результирующего движе-

ния точки.

Ответ: x² /4 + y²/4 = 1 − уравнение окружности радиусом R = 2 м.

15.(В.12.40). Точка участвует в двух взаимно перпндикулярных колебаниях

x = cos πt и y =cos πt/2. Найти траекторию результирующего движения точки.

Ответ: 2y² − x =1 − уравнение параболы.

16.(В.12.53). Тело массой m = 10 г совершает затухающие колебания с мак-

симальной амплитудой Аmax = 7 см, начальной фазой φ = 0 и коэффициентом

затухания β = 1.6 сˉ¹. На это тело начала действовать внешняя периодическая

сила F, под действием которой установились вынужденные колебания. Уравне-

ние вынужденных колебаний имеет вид х = 5 sin(10πt − 3π/4) см. Найти (с чис-

ловыми коэффтциентами) уравнение собственных колебаний и закон измене-

ния внешней периодической силы F(t).

− 1.6t

Ответ: x = 7 e sin 10.5πt см; F = 72 sin 10πt мН.

17.(В.12.55). По грунтовой дороге прошел трактор, оставив следы в виде

ряда углублений, находящихся на расстоянии l = 30 см друг от друга. По этой

дороге покатили детскую коляску, имеющую две одинаковые рессоры, каждая

из которых прогибается на хо = 2 см под действием груза массой mo = 1 кг. С

какой скоростью катили каляску, если от толчков на углублениях она, попав в

резонанс, начала сильно раскачиваться? Масса коляски М =10 кг.

Ответ: v = 1.7 км/ч. 50

18.(В.12.60). Уравнение незатухающих колебаний имеет вид х = sin 2.5πt

см. Найти смещение х от положения равновесия, скорость v и ускорение a

точки, находящейся на рассоянии l = 20 м от источника колебаний, для мо-

мента времени t = 1c после начала колебаний. Скорость распространения ко-

лебаний с = 100 м/c.

Ответ: x = 0; v = 7.85 см/c; a = 0.

19.(В.12.62). Найти разность фаз Δφ колебаний двух точек, лежащих на лу-

че и отстоящих на расстоянии l = 2 м друг от друга, если длина волны λ = 1 м.

Ответ: Δπ = 4π.

20.(В.12.65). Найти положение узлов и пучностей и начертить график сто-

ячей волны, если: а) отражение происходит от менее плотной среды; б) отра-

жжение происходит от более плотной среды. Длина бегущей волны λ = 12 см.

Ответ: а) хузл = 3, 9, 15, … см; xпуч = 0, 6, 12, 18, … см;

б) хузл = 0, 6, 18, … см; xпуч = 3, 9, 15, … см.

ЗАДАЧИ ГРУППЫ Б

1.(Ч.6.2). Определить период Т, частоту v и начальную фазу φ ко-

лебаний, заданных уравнением х = А sinω(t + τ), где ω =2.5π сˉ¹, τ = 0.4 с.

Ответ: T = 0.8 c; v = 1.24 Гц; φ = π рад.

2.(Ч.6.8). Определить максимальные значения скорости vmax и ускоре-

ния аmax точки, совершающей гармонические колебания с амплитудой А =

= 3 см и циклической частотой ω = π/2 cˉ¹.

Ответ: vmax = 4.71 см/c; amax = 7.40 см/c².

3.(Ч.6.13) Колебания точки происходят по закону х = А cos(ωt + φ). В

некоторый момент времени смещение х точки равно 5 см, её скорость dx/dt=

= 20 см/c и ускорение d²x/dt² = − 80 см/c². Найти амплитуду А, угловую час-

тоту ω, период Т колебаний и фазу (ωt + φ) в рассматриваемый момент

времени.

Ответ: ω = √ (− d²x/dt²)/x = 4 cˉ¹; T = 2π/T = 1.57 c; A = √(dx/dt)²+ ω²x² =

= 7.07 cм; ωt + φ = arccos(x/A) = π/4 рад.

4.(Ч.6.20). Складываются два гармонических колебания одинаковой часто-

ты и одинакового направления:

x1 = A1 cos(ωt + φ1) и х2 = А2 cos(ωt + φ2).

Начертить векторную диаграмму для момента времени t = 0. Определить

аналитически амплитуду А и начальную фазу φ результирующего колеба-

ния. Отложить А и φ на векторной диаграмме. Найти уравнение результи-

рующего колебания (в тригонометрической форме). Задачу решить для двух

случаев: 1) А1 = 1 см, φ1 = π/3; A2 = 2 см, φ2 = 5π/6; 2) A1 = 1 см, φ1 =2π/3;

A2 = 1 см, φ2 = 7π/6.

Ответ: 1) A =2.24 см, φ = 0.686π рад; 2) A = 1.41 см, φ = 0.917π рад;

x = Acos(ωt + φ). 51

5.(Ч.6.27). Движение точки задано уравнениями х = А1 sinωt и у =

= А2sinω(t + τ), где А1 = 10 см, А2 = 5 см, ω = 2 сˉ¹, τ = π/4 c. Найти урав-

нение траектории и скорость точки в момент времени t = 0.5 с.

Ответ: x²/100 + y²/25 = 1, v = 13.7 см/c.

6.(Ч.6.28). Материальная точка участвует одновременно в двух взаим-

но перпендикулярных колебаниях, выражаемых уравнениями х = А1 cosωt и

у = − А2 cos2ωt, где А1 = 2 см, А2 = 1 см. Найти уравнение траектории и по-

строить её.

Ответ: y = − 2(A2/A1)x² + A2, y = − x²/2 + 1.

7.(Ч.6.37). К спиральной пружине подвесили грузик, в результате чего

пружина растянулась на х = 9 см. Каков будет период Т колебаний грузи-

ка, если его немного оттянуть вниз и затем отпустить?

Ответ: T = 0.6 c.

8.(Ч.6.38). Гиря, подвешенная к пружине, колеблется по вертикали с

амплитудой А = 4 см. Определить полную энергию Е колебаний гири, ес-

ли жесткость k пружины равна 1 кН/м.

Ответ: Е = 0.8 Дж.

9.(Ч.6.40). Математический маятник длиной l= 1 м установлен в лиф-

те. Лифт поднимается с ускорением а = 2.5 м/c². Определить период Т ко-

лебаний маятника.

Ответ: T = 1.8 c.

10.(Ч.6.60). Гиря массой m = 500 г, подвешенная к спиральной пружине

жёсткостью k = 20 Н/м, совершает упругие колебания в некоторой среде. Ло-

гарифмический декремент затухания δ = 0.004. Определить число N пол-

ных колебаний, которые должга совершить гиря, чтобы амплитуда колебаний

уменьшилась в n =2 раза. За какое время t произойдет это уменьшение?

Ответ: N = 173; t = 2 мин 52 с.

11.(Ч.6.71). Пружинный маятник (жёсткость k пружины равна 10 Н/м,

масса m груза равна 100 г) совершает вынужденные колебания в вязкой сре-

де с коэффициентом сопротивления r = 2·10ˉ² кг/c. Определить коэффициент

затухания β и резонансную амплитуду Арез, если амплитудное значение вы-

нуждающей силы Fo = 10 мН.

Ответ: β = 0.1 cˉ¹; Aрез = 5 см.

12.(Ч.7.7). Волна с периодом Т = 1.2 с и амплитудой колебаний А = 2 см

распространяется со скоростью v = 15 v/c.Чему равно смещение ξ (х,t) точки,

находящейся на расстоянии х = 45 м от источника волн, в тот момент, когда

от начала колебаний источника прошло время t = 4 c?

Ответ: ξ = − 1.73 см.

13.(Ч.7.11). Определить скорость v распространения волны в упругой

среде, если разность фаз Δφ колебаний двух точек среды, отстоящих друг от

друга на Δх = 10 см, равна π /3. Частота колебаний v равна 25 Гц.

Ответ: v = 15 м/c. 52

14.(Ч.7.22). Определить длину λ бегущей волны, если в стоячей волне

расстояние l между: 1) первой и седьмой пучностями равно 15 см; 2) пер-

вым и четвертым узлами равно 15 см.

Ответ: 1) λ = 5 см; 2) λ = 10 см.

15.(Ч.7.17). Скорость звука в некотором газе при нормальных условиях

равна 308 м/c. Плотность ρ газа равна 1.78 кг/м³. Определить отношение

ср/cv для данного газа.

Ответ: 1.67.

ЗАДАЧИ ГРУППЫ С

1.(И.4.3). Частица совершает гармонические колебания вдоль оси х око-

ло положения равновесия х =0. Частота колебаний ω = 4.00 рад/c. В неко-

который момент координата частицы хо = 25.0 см и её скорость vxo = 100

см/c. Найти координату х и скорость vx частицы через t = 2/40 c после

этого момента.

Ответ: x = − 29 см; vx = − 81 cм/c.

2.(Ч.6.47). Из тонкого однородного диска радиусом R =20 см вырезана

часть, имеющая вид круга радиусом r = 10 см, так, как это показано на рис.35.

Рис. 35

Оставшаяся часть диска колеблется относительно горизонтальной оси О, совпа-

дающей с одной из образующих цилиндрической поверхности диска. Найти пе-

риод Т колебаний такого маятника.

Ответ: T = 1.14 c.

3.(И.4.11). Точка движется в плоскости ху по закону х= А sinωt, у =

= В cosωt, где А, В и ω − положительные постоянные. Найти: 1) уравнение

траектории точки у(х) и направление её движения по этой траектории; 2) ус-

корение а в зависимости от её радиус-вектора r относительно начала коор-

динат.

Ответ: 1) х²/A² + y²/B² = 1, по часовой стрелке; 2) a = − ω²r.

4.(И.4.13). Частица массы m находится в одномерном силовом поле, где

её потенциальная энергия зависит от координаты х как U(x) = Uo (1 − cosax),

Uo и а − постоянные. Найти период малых колебаний частицы около положе-

ния равновесия.

Ответ: T =2π√m/a²Uo .

5.(И.4.14). Тот же вопрос, что и в предыдущей задаче, но потенциальная

энергия имеет вид U(x) = a /x² − b/x, где а и b − положительные постоянные.

Ответ: T =4πa(√ 2ma)/b².

6.(И.4.19). Жидкость объёмом V = 16 см³ налита в изогнутую U-образ-

ную трубку (рис.36) с площадью сечения канала S = 0.50 см². Пренебрегая

вязкостью, найти период малых колебаний жидкости.

Ответ: T = π√2V/Sg = 0.8 c.

7.(И.4.21). Вычислить период малых колебаний ареометра (рис.37), ко-

торому сообщили небольшой толчок в вертикальном направлении. Масса арео-

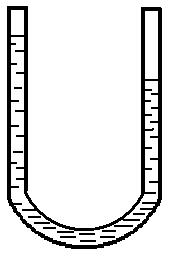
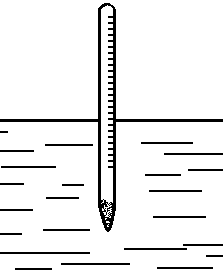
Рис.36 Рис. 37

метра m = 50 г, радиус его трубки r = 3.2 мм, плотность жидкости ρ = 1.00

г/см³. Сопротивление жидкости пренебрежимо мало.

Ответ: T = √4πm/ρgr² = 2.5 с.

8. Сплошной однородный цилиндр массы m совершает малые колебания

под действием двух пружин, общий коэффициент жесткости которых равен k

(рис. 38). Найти период этих колебаний в отсутствие проскальзывания.

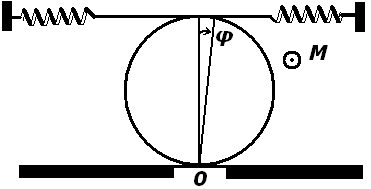
Рис. 38

Ответ: T = π√3m/2k.

9.(И.4.76). Математический маятник совершает колебания в среде, для

которой логарифмический декремент затухания δо = 1.50. Каким будет зна-

чение δ, если сопротивление среды увеличить в n = 2.00 раза? Во сколько

раз n΄ следует увеличить сопротивление среды, чтобы колебания стали невоз-

можны?

Ответ: δ = nδo/[√1 + (1 − n²)(δo/2π)²] =3.3; n΄ = √1 + (2π/δo)² = 4.3 раза.

10.(И.4.80). Найти добротность математического маятника длины l = 50

см, если за промежуток времени τ = 5.2 мин его полная механическая энергия

уменьшилась в η = 4.0∙10²*² раз.

Ответ: Q≈ 1/2√4gτ²/l lnη − 1 = 1.2∙10².

11.(И.4.90). Шарик массы m, подвешенный к пружинке, удлиняет её

на Δl. Под действием внешней вертикальной силы, меняющейся по гармони-

ческому закону с амплитудой Fo, шарик совершает вынужденные колебания.

Логарифмический декремент затухания δ. Пренебрегая массой пружинки,

найти частоту ω вынуждающей силы, при которой амплитуда а смещения

шарика максимальна. Каково значение этой амплитуды? 54

Ответ: ωрез = √ {[1−(δ/2π)²]/[ 1 + (δ/2π)²]}(g/Δl);

aрез =(δFoΔl/4πmg)( 1 + 4π²/δ²).

12. Шарик массы m = 50 г подвешен на невесомой пружине жесткостью

k = 20 Н/м. Под действием вынуждающей вертикальной гармонической си-

лы с циклической частотой ω1 = 18 сˉ¹ он совершает установившиеся вынуж-

денные колебания с амплитудой Хо1 = 1.3 см. При этом смещение шарика от-

стаёт по фазе от вынуждающей силы на α1 = π/4. Найти работу вынуждающей

силы за время, равное периоду колебаний. Во сколько раз найденное значение

меньше той максимальной работы, которую может совершить вынуждающая

сила за период?

Ответ: А1 = Хо1²mπ(ωo² − ω1²), ωо = √k/m − собственная циклическая час-

тота осциллятора; A1 = 2.0∙10ˉ³ Дж. Аmax/A1 = 2ω1/ωo = 1.8.

13.(И.4.94). Амплитуды смещений вынужденных гармонических колеба-

ний при частотах ω1 = 400 сˉ¹ и ω2 = 600 сˉ¹ равны между собой. Найти

частоту ω, при которой амплитуда смещения максимальна.

Ответ: ωрез = √(ω1² + ω2²)/2 = 5.1∙10² cˉ¹.

14.(И.4.169). За сколько времени звуковые колебания пройдут расстояние

l между точками А и В, если температура воздуха между ними меняется ли-

нейно от Т1 до Т2? Скорость звука в воздухе v = α√T, где α − постоянная.

Ответ: t = 2l/[α(√T1 + √T2)].

15.(И.4.171). Найти волновой вектор k и скорость v волны, имеющей

вид ξ = а cos(ωt − αx − βy − γz).

Ответ: k = α i + β j + γk, v = ω/√α² + β² + γ², где i, j, k − орты осей ко-

ординат. Занятие 4. Динамика вращательного движения

твердого тела

СОДЕРЖАНИЕ ТЕОРИИ

10. Момент силы, момент инерции, момент импульса материальной

точки и твердого тела относительно оси вращения.

11. Уравнение динамики вращательного движения.

12. Собственный, орбитальный и полный моменты импульса относи-

тельно оси вращения.

13. Закон сохранения момента импульса.

14. Работа и мощность момента силы.

15. Кинетическая энергия вращательного и плоского движения.

16. Гироскопы. Частота прецессии гироскопа.

ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ