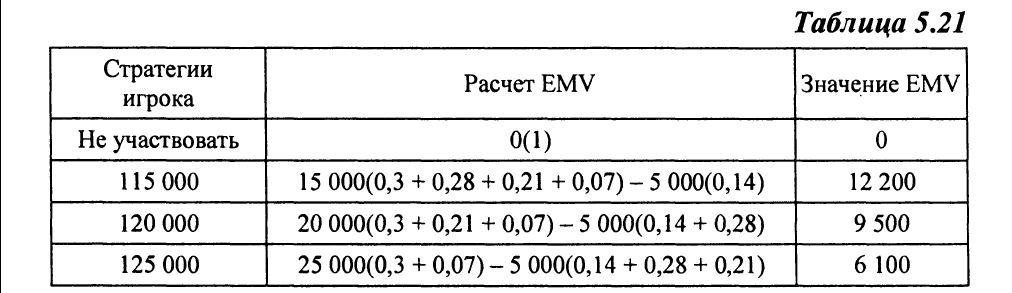
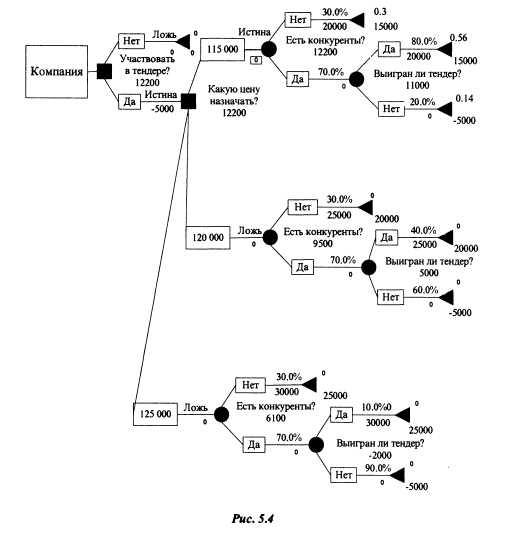
1.Принципы решения многошаговых игр, задача с выбором оптимальной стратегии участия в тендере. Использование программы TreePlan.

2.Примеры задач линейного программирования.

3. Понятие задачи линейного программирования. Различные формы её записи и их эквивалентность

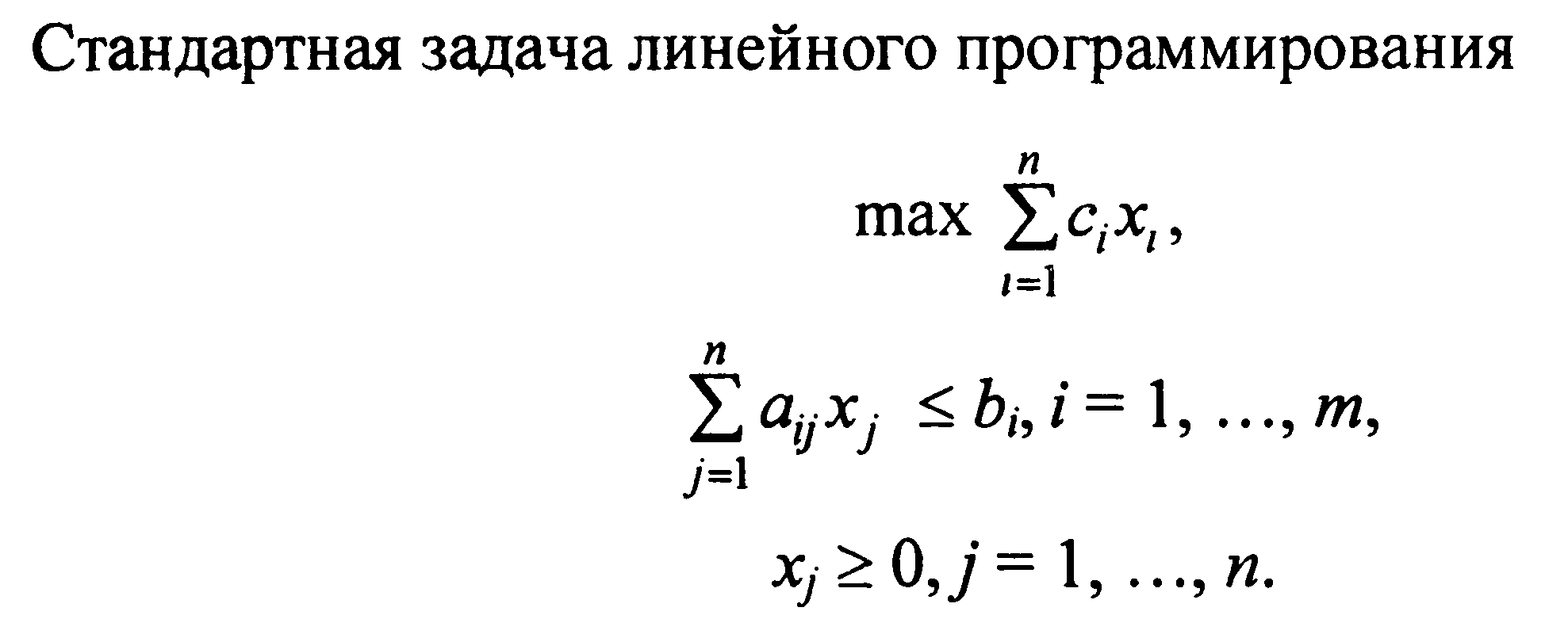
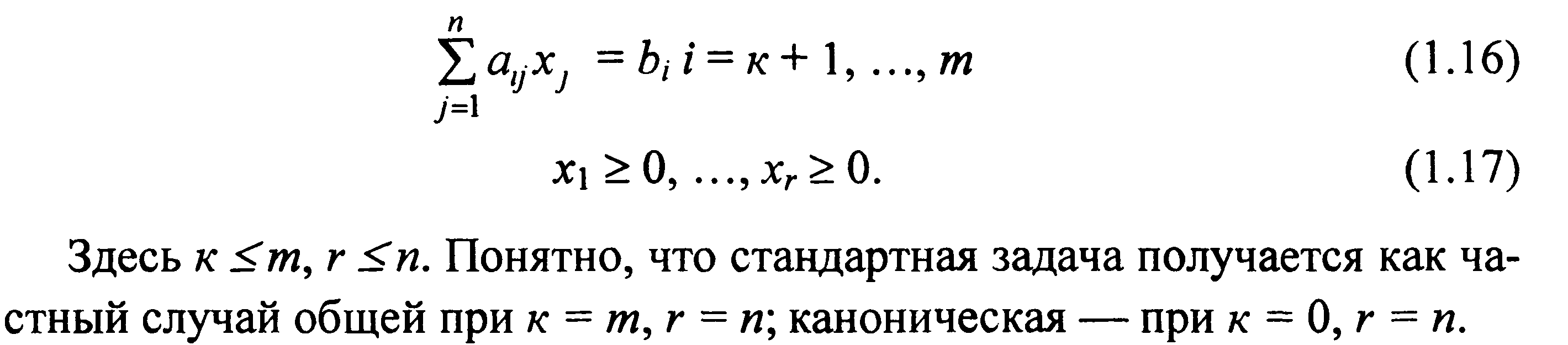
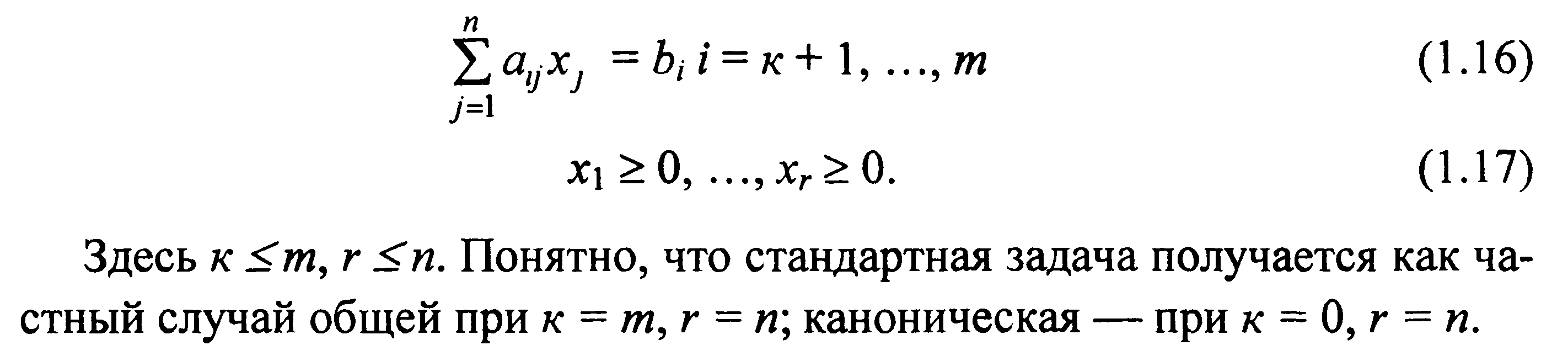
4.Геометрический метод решения простейших ЗЛП

Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения ЗЛП имеет очень узкие рамки применения.

Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации.

1. Сформулировать ЗЛП.

2. Построить на плоскости {х₁, х₂} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

3. Найти полуплоскости, определяемые каждым из ограничений задачи.

4. Найти область допустимых решений.

5. Построить прямую c₁x₁ + c₂x₂ = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений.

6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений.

7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.

Далее рассмотрим пример решения ЗЛП графическим методом.

1. Сформулируем задачу:

= 2x₁ + 4x₂ → max;

4x1 +6x2 ≤ 120, 2x1 +6x2 ≤ 72, x2 ≤ 10;

x₁ ≥ 0,   x₂ ≥ 0.

2. Теперь построим прямые, соответствующие каждому из функциональных ограничений задачи (см. рисунок 2.1). Эти прямые обозначены на рисунке (1), (2) и (3).

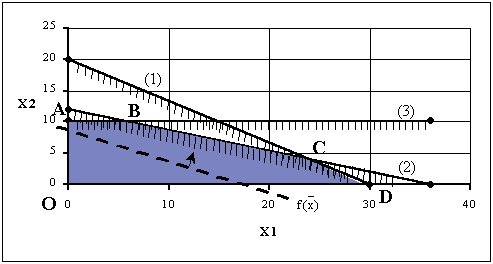
Рисунок 2.1 - Геометрическое решение ЗЛП

3. Штрихи на прямых указывают полуплоскости, определяемые ограничениями задачи.

4. Область допустимых решений включает в себя точки, для которых выполняются все ограничения задачи. В нашем случае область представляет собой пятиугольник (на рисунке обозначен ABCDO и окрашен синим цветом).

5. Прямая, соответствующая целевой функции, на рисунке представлена пунктирной линией.

6. Прямую передвигаем параллельно самой себе вверх (направление указано стрелкой), поскольку именно при движении в этом направлении значение целевой функции увеличивается. Последней точкой многоугольника решений, с которой соприкоснется передвигаемая прямая, прежде чем покинет его, является точка C. Это и есть точка, соответствующая оптимальному решению задачи.

7. Осталось вычислить координаты точки С. Она является точкой пересечения прямых (1) и (2). Решив совместно уравнения этих прямых, найдем: , . Подставляя найденные величины в целевую функцию, найдем ее значение в оптимальной точке .

Таким образом, для максимизации прибыли компании следует ежедневно выпускать 24 клюшки и 4 набора. Реализация такого плана обеспечит ежедневную прибыль в размере $64.

ИЛИ

5.Опорные точки допустимого множества канонической задачи линейного программирования. Основная идея симплекс-метода.

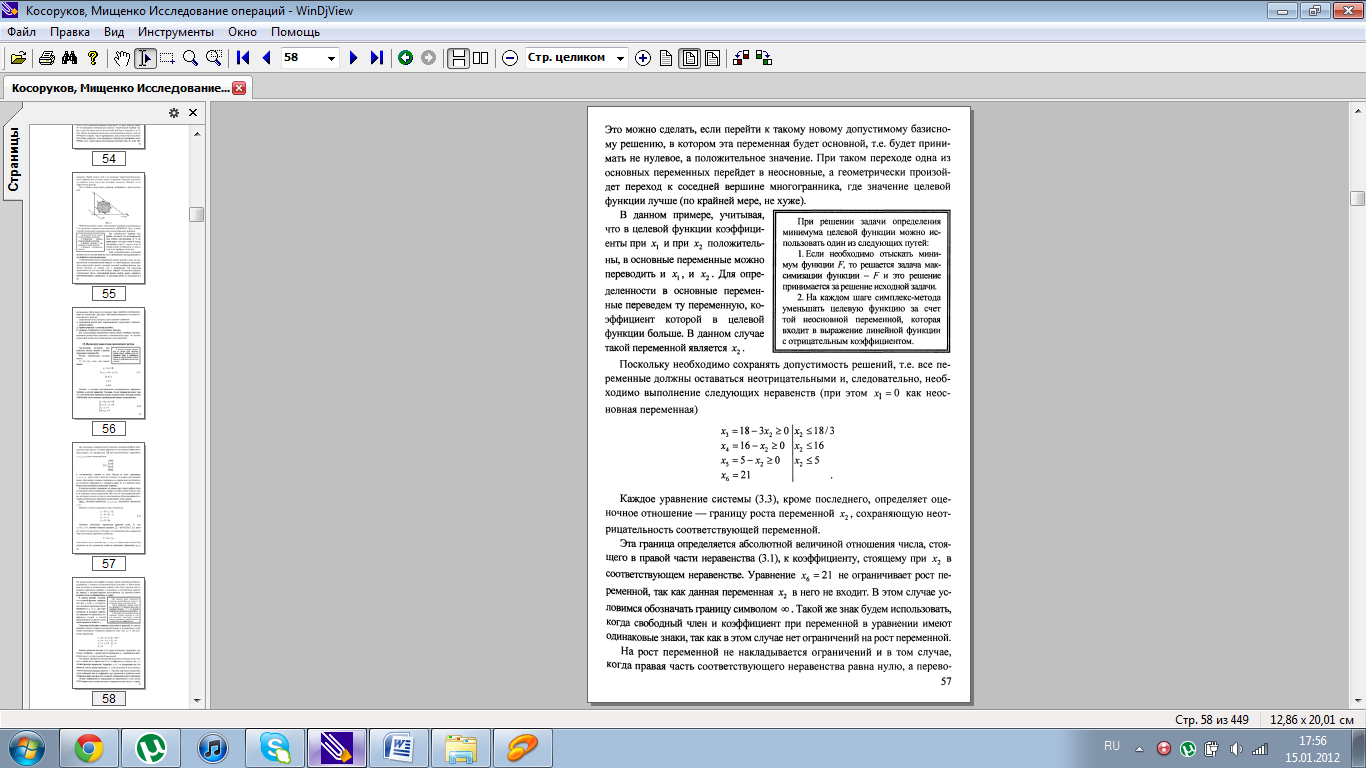
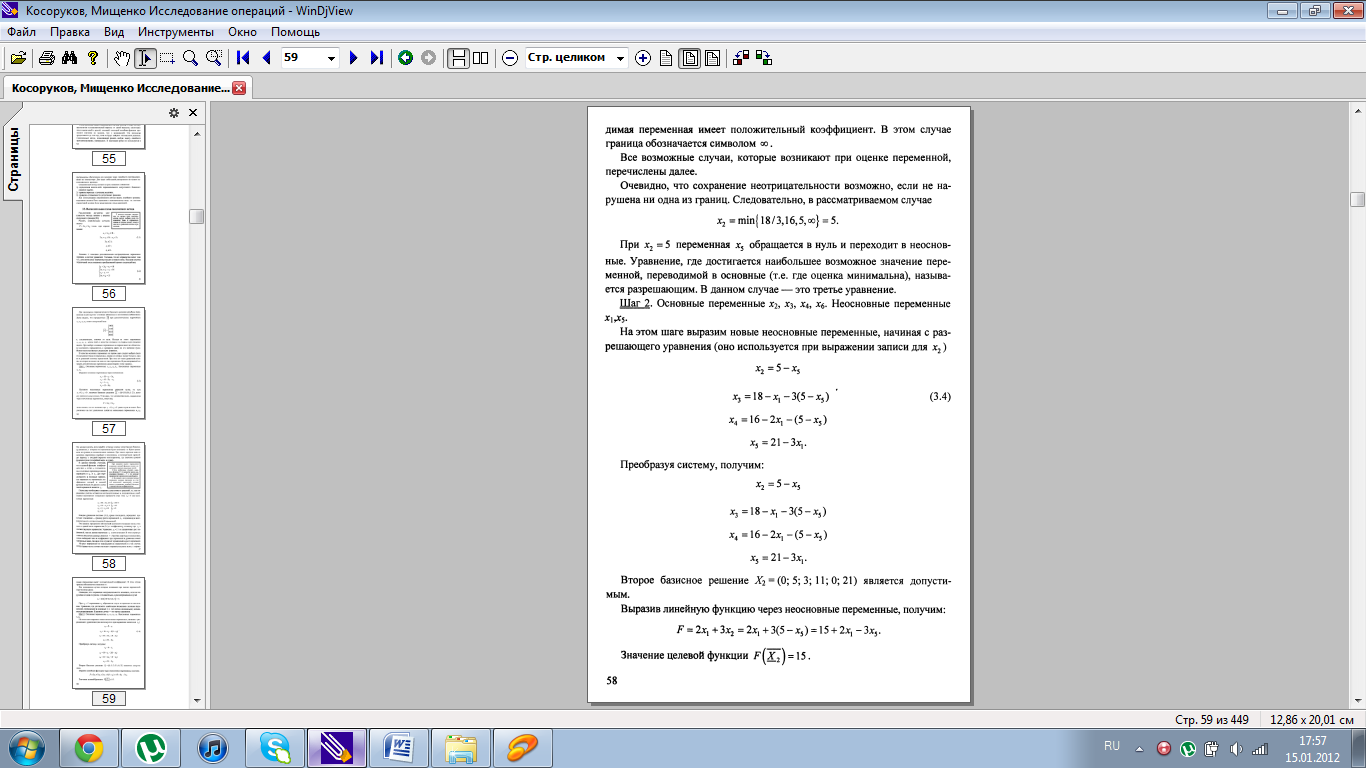
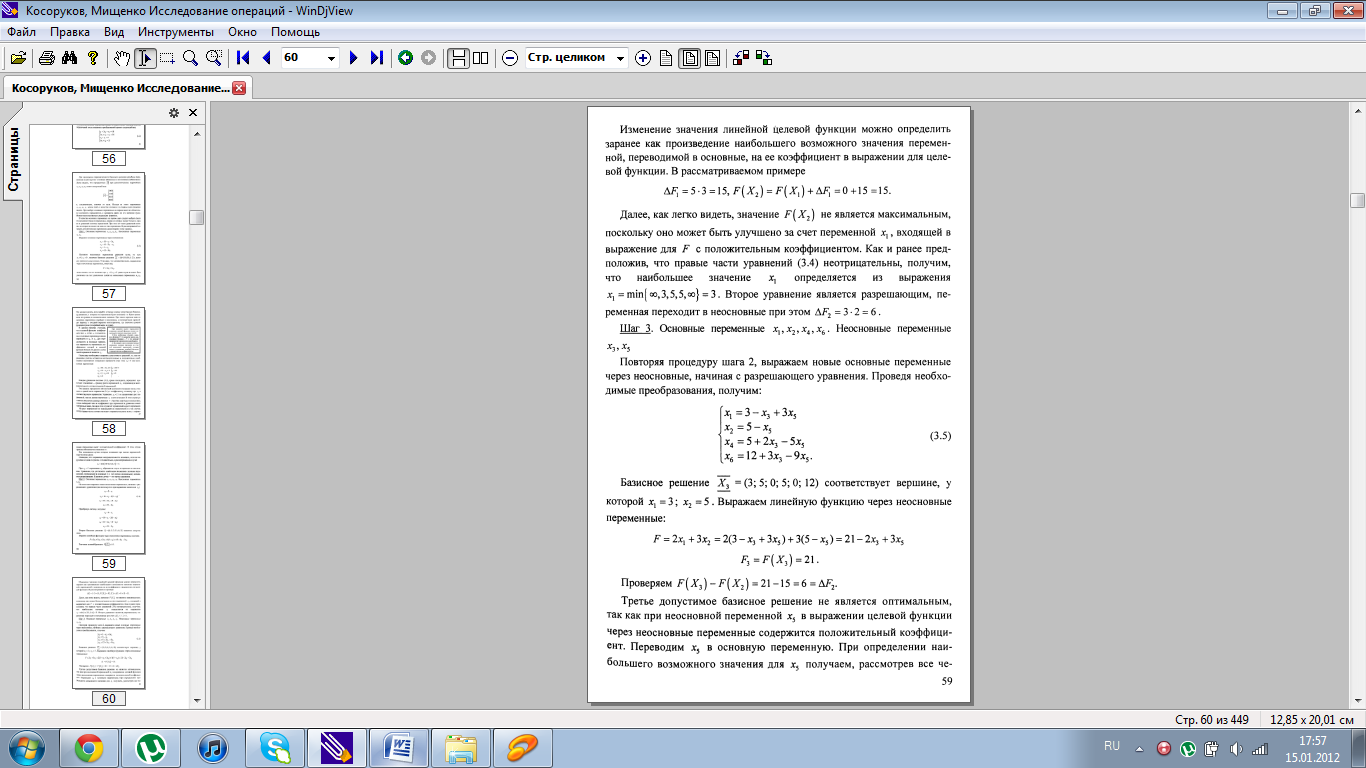
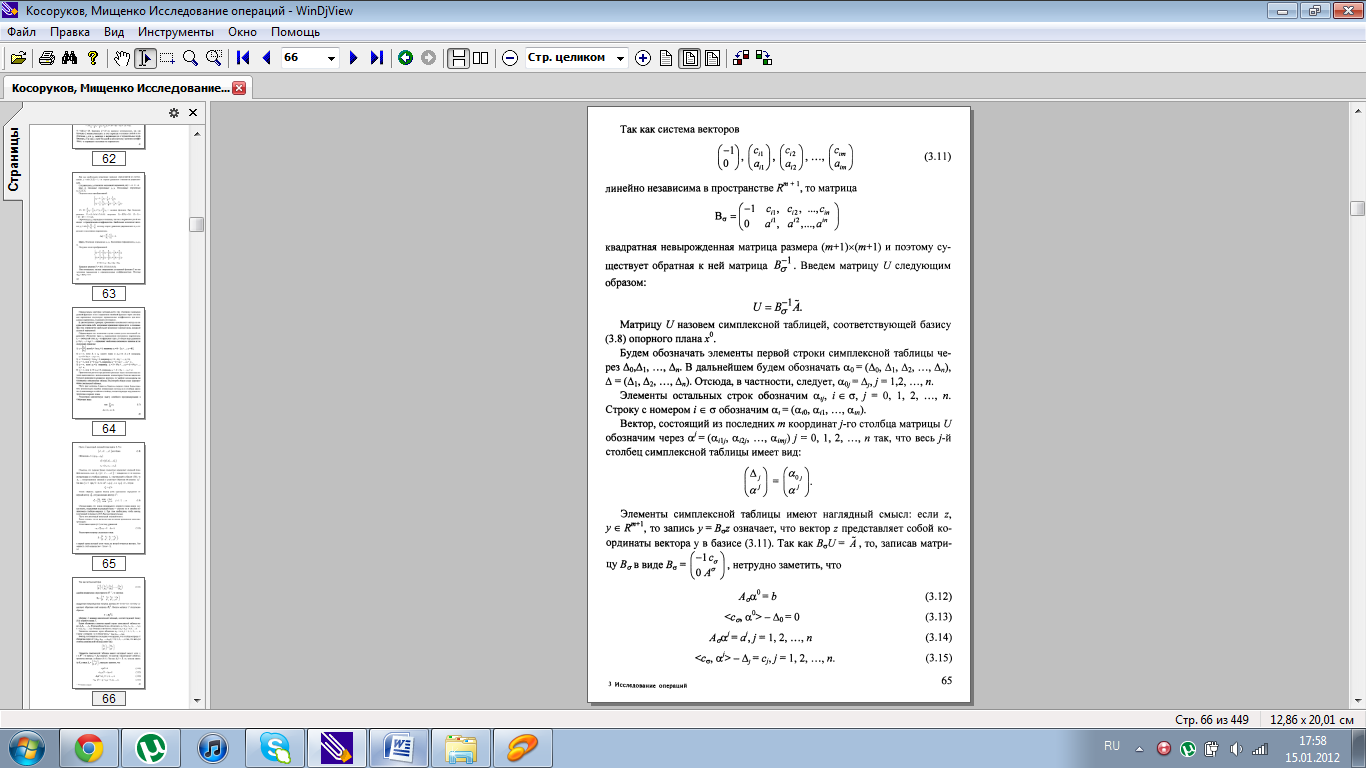
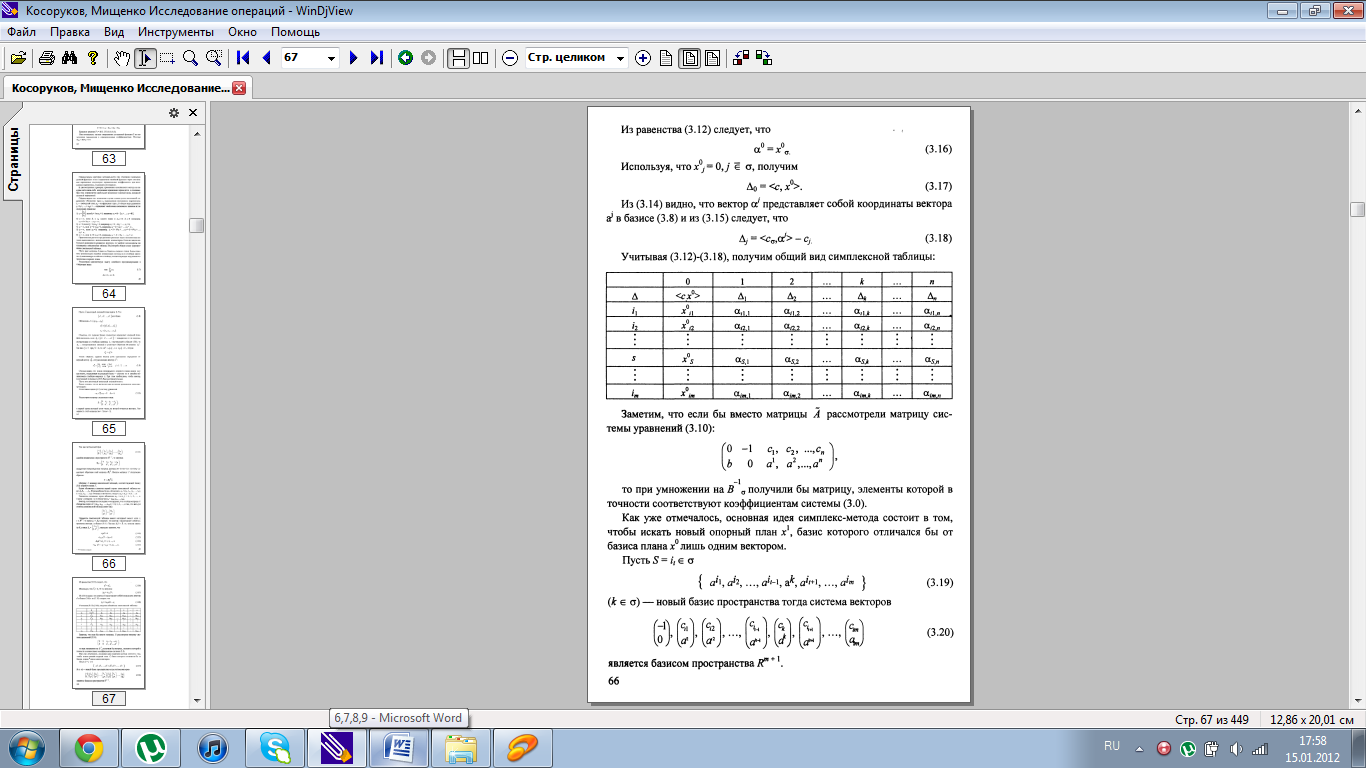
Основная идея симплекс-метода достаточно просто иллюстрируется геометрически. Как уже говорилось выше, допустимое множество задачи ЛП (1.2- 1.3) представляет собой выпуклый многогранник (в случае, если множество не ограничено – выпуклое многогранное множество) с конечным числом вершин этого многогранника, т.е. его крайних точек.  В том случае, если задача ЛП имеет единственное решение, то решение находится в одной из этих вершин.  Симплекс-метод состоит в таком направленном переборе вершин, при котором  значение целевой функции улучшается  (не ухудшается) при переходе от вершины к вершине. Каждая вершина многогранника является пересечением плоскостей (в n-мерном случае – гиперплоскостей), каждая из которых задается уравнением, определенным  соответствующим ограничением исходной задачи ЛП. Другими словами, каждая вершина определяется системой уравнений, выбираемой специальным образом из системы неравенств (1.1). Таким образом, симплекс-метод, по сути дела, представляет собой вычислительную процедуру последовательного решения систем линейных уравнений.  Поэтому этот метод содержит в себе правила формирования систем уравнений (в терминах разобранной ниже схемы – правило выбора разрешающего элемента) и схему решения систем линейных уравнений (в терминах приведенной ниже схемы – жордановы исключения).

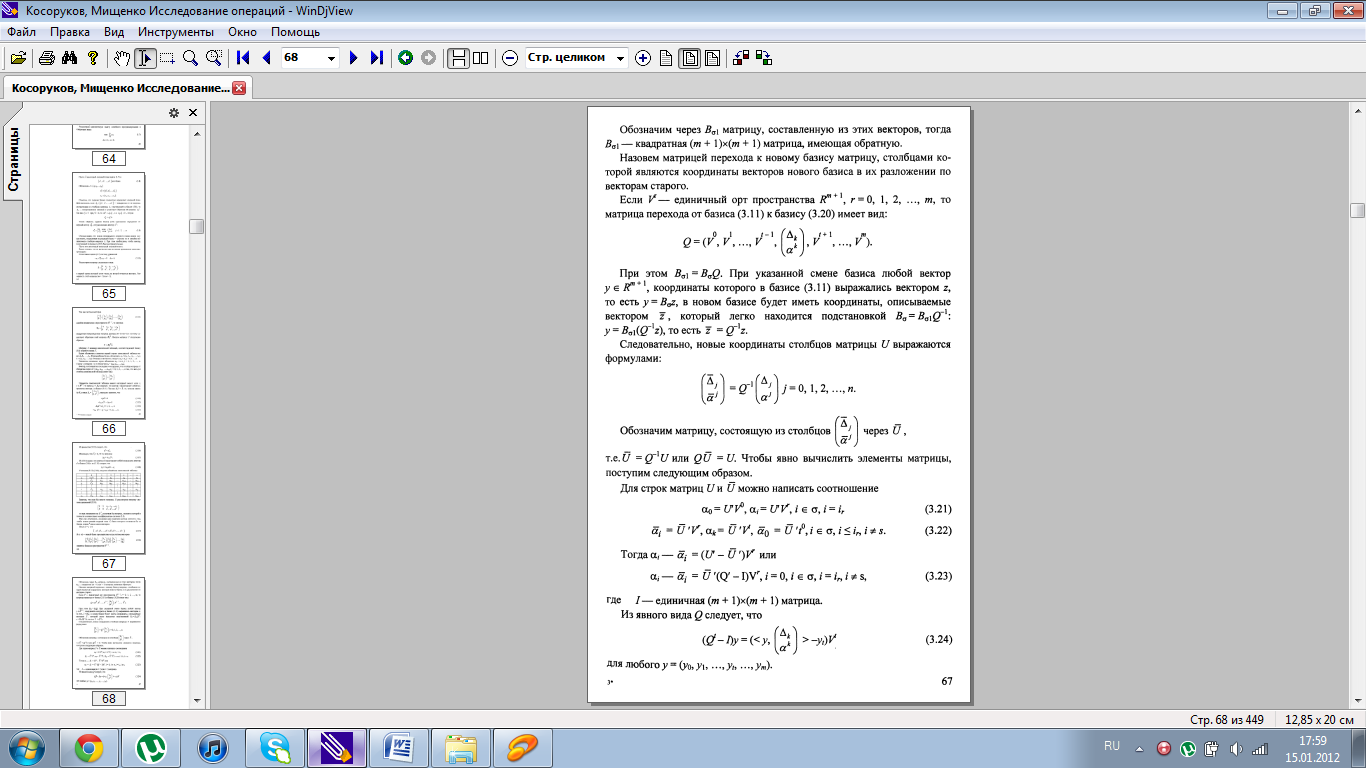
6. Описание симплекс-метода.

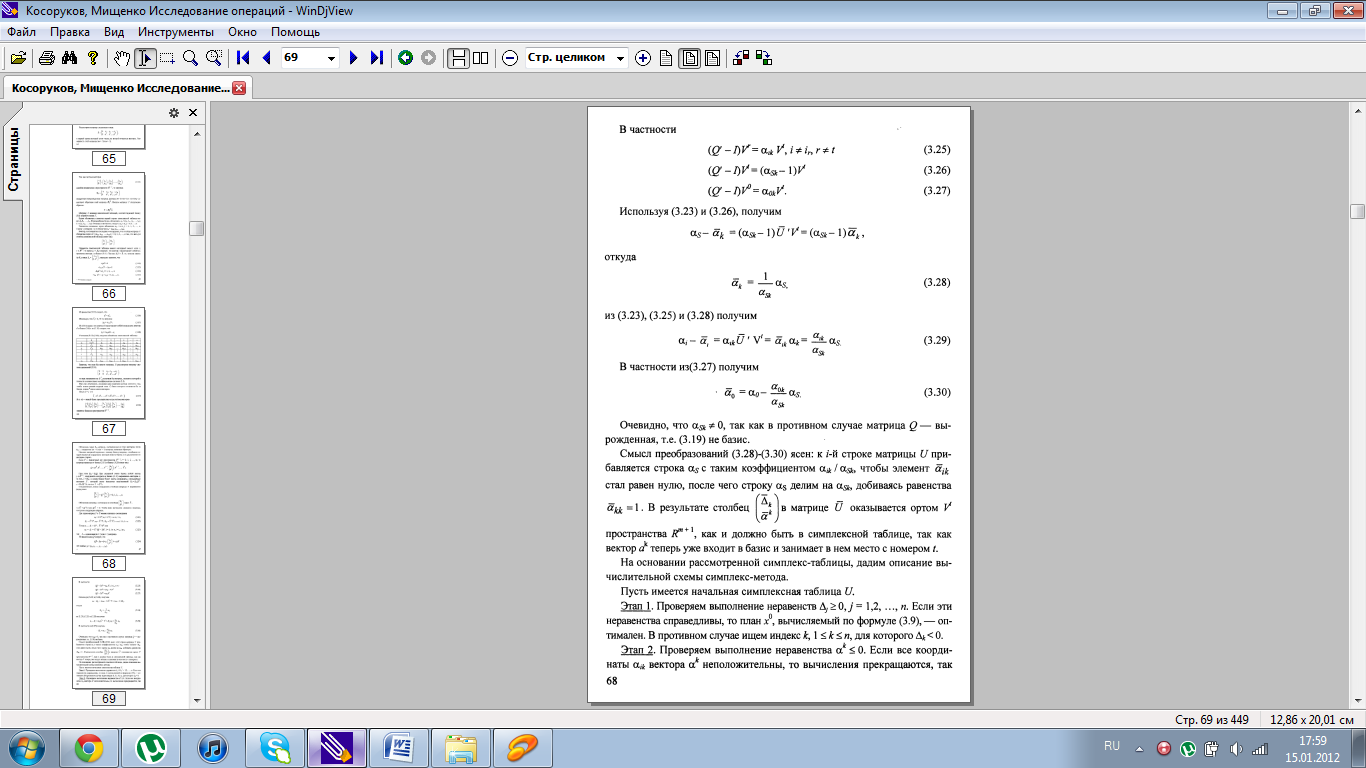
7. Методы поиска начальной опорной точки.

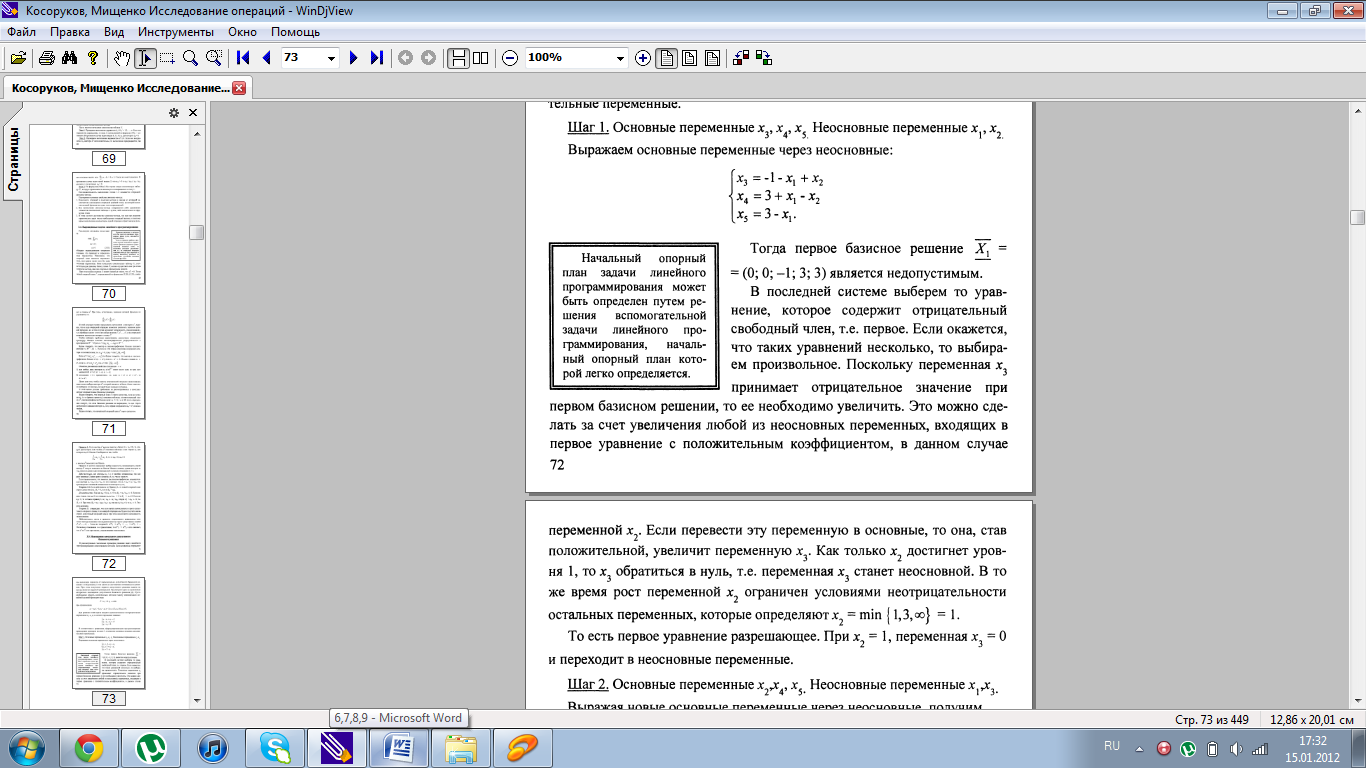
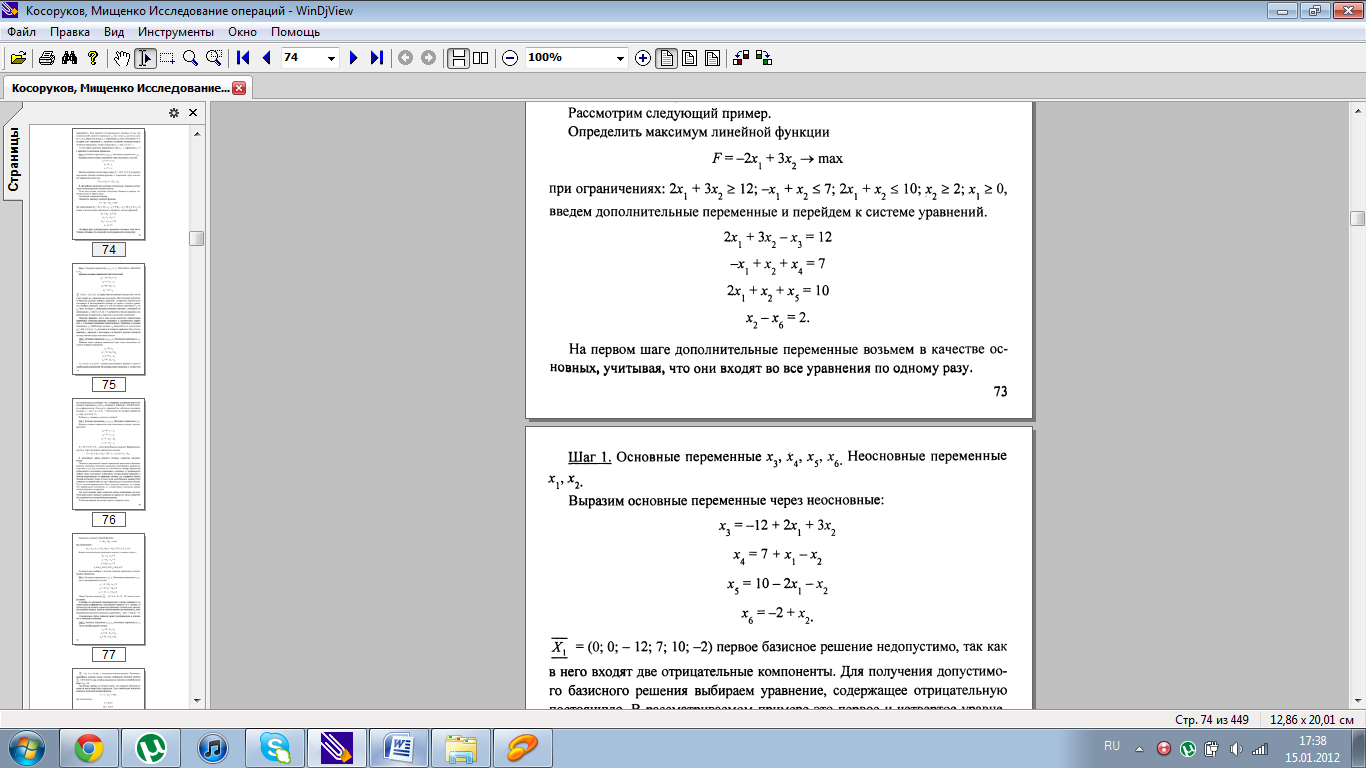
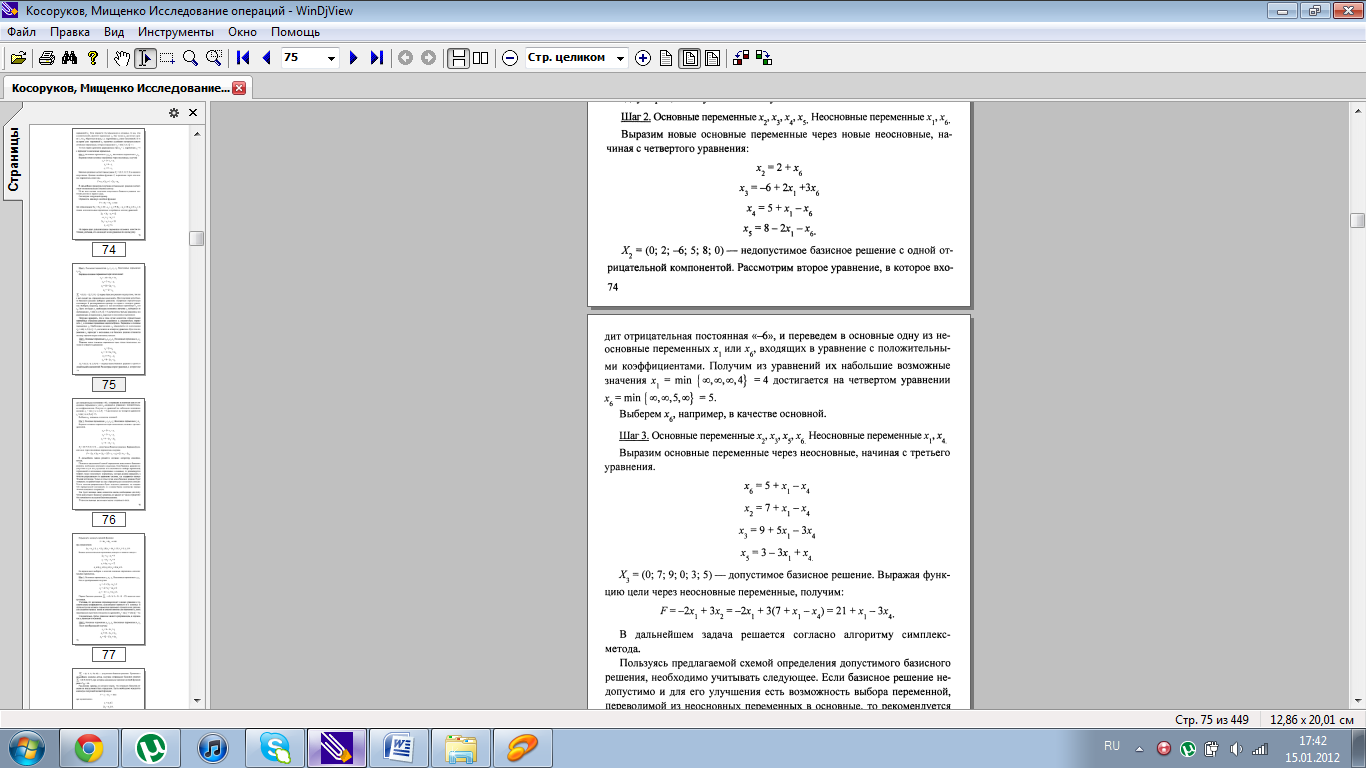
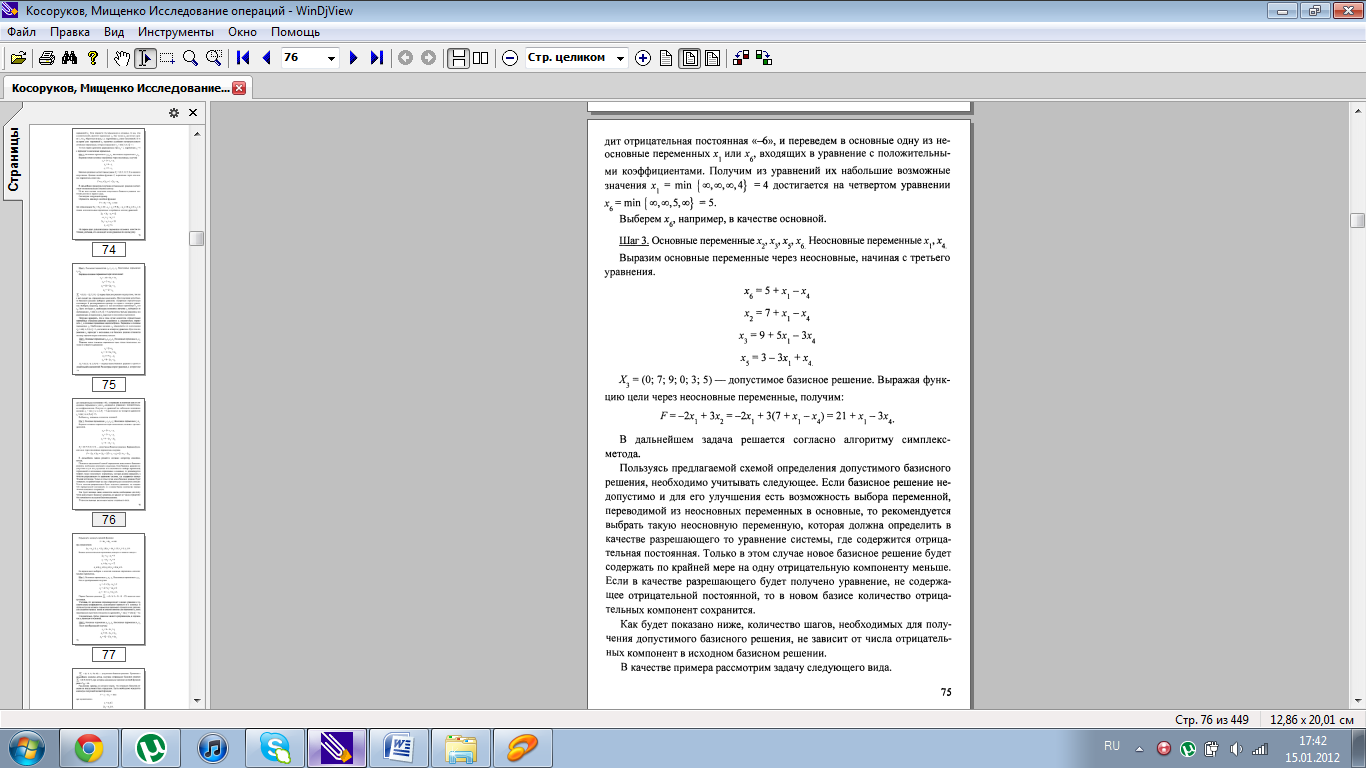
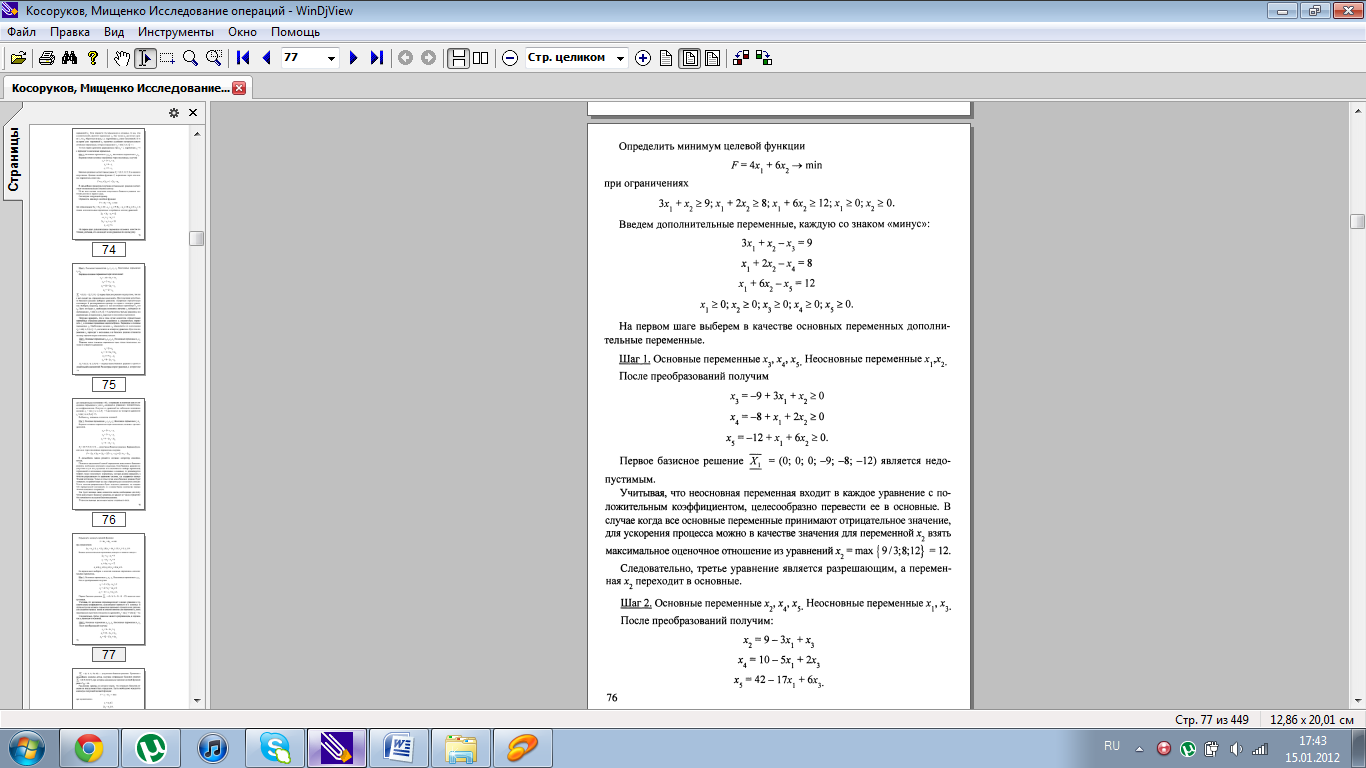
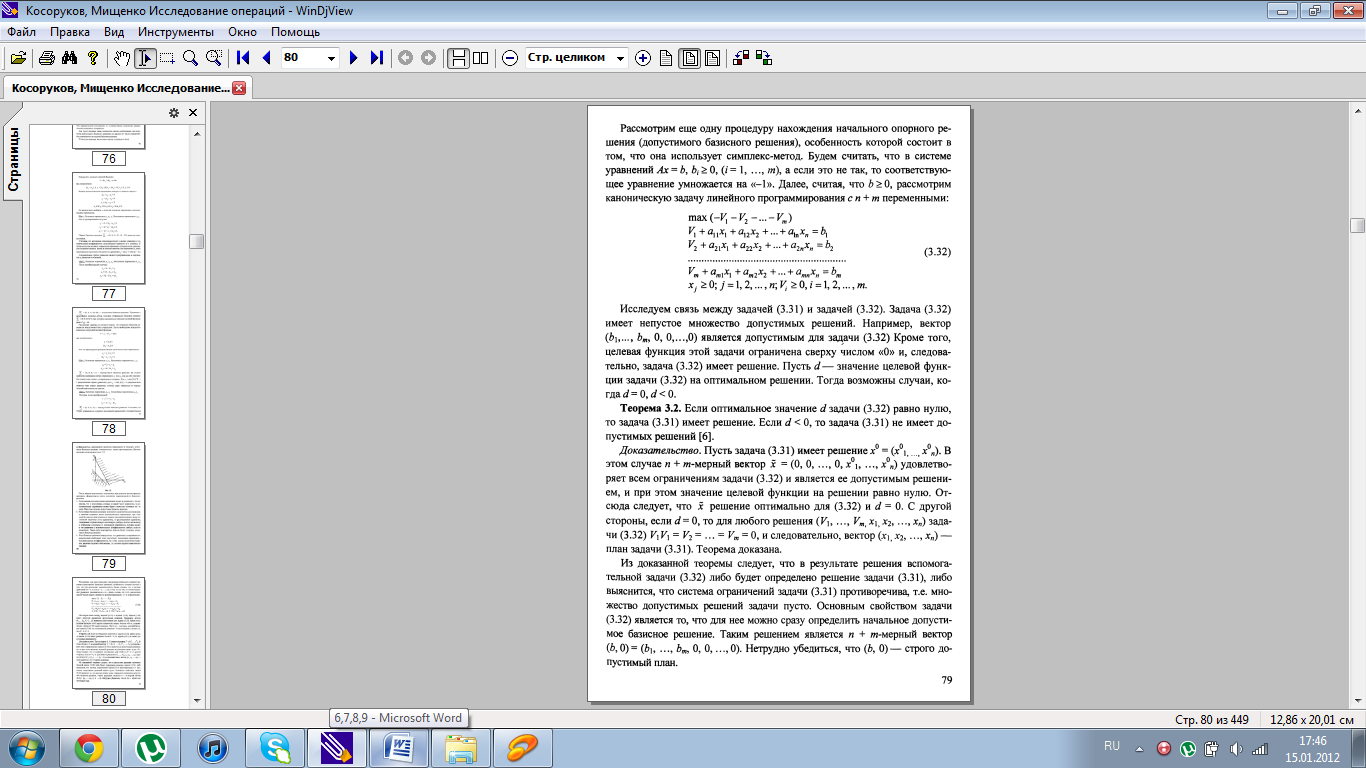
8. Понятие вырожденности в теории линейного программирования.

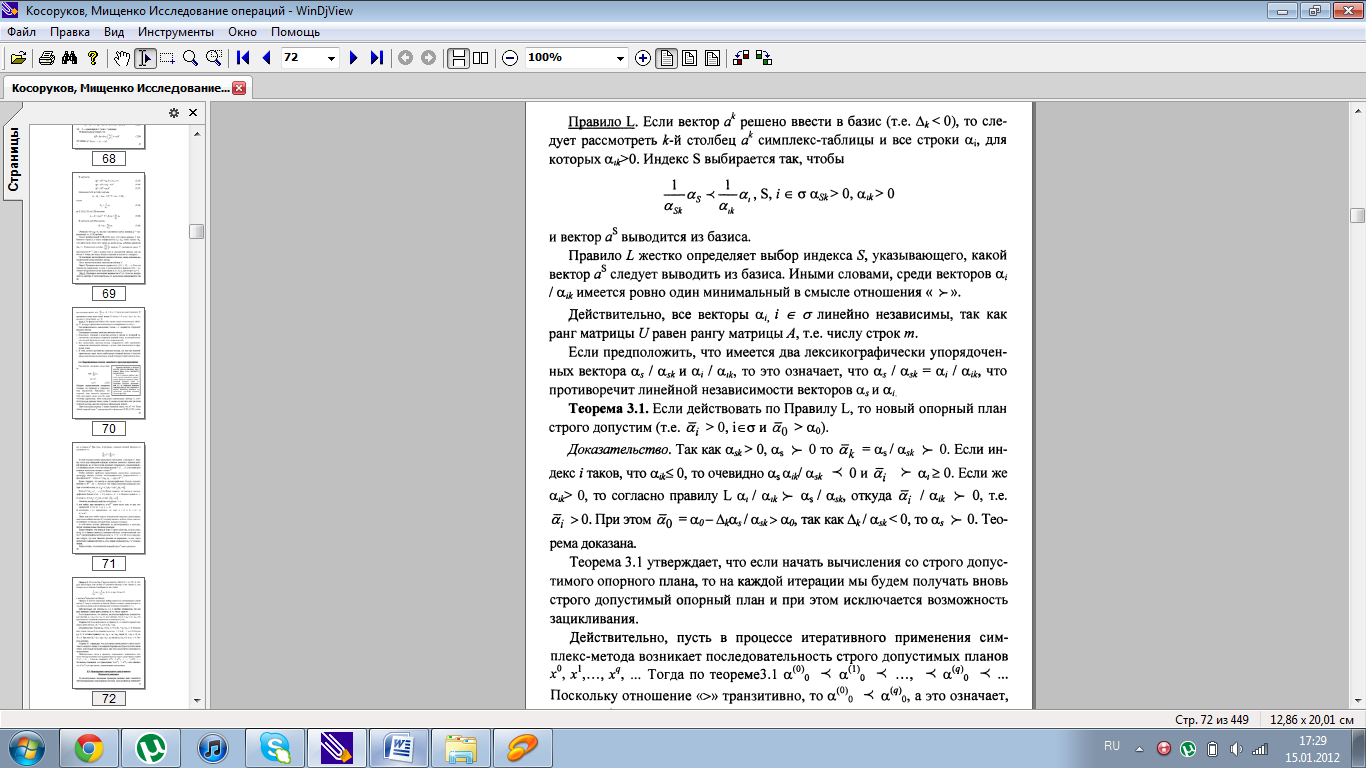
9. Примеры использования теории двойственности в линейном программировании. Исследование на оптимальность данной допустимой точки, предварительное решение двойственной задачи, совместное решение прямой и двойственной задачи.

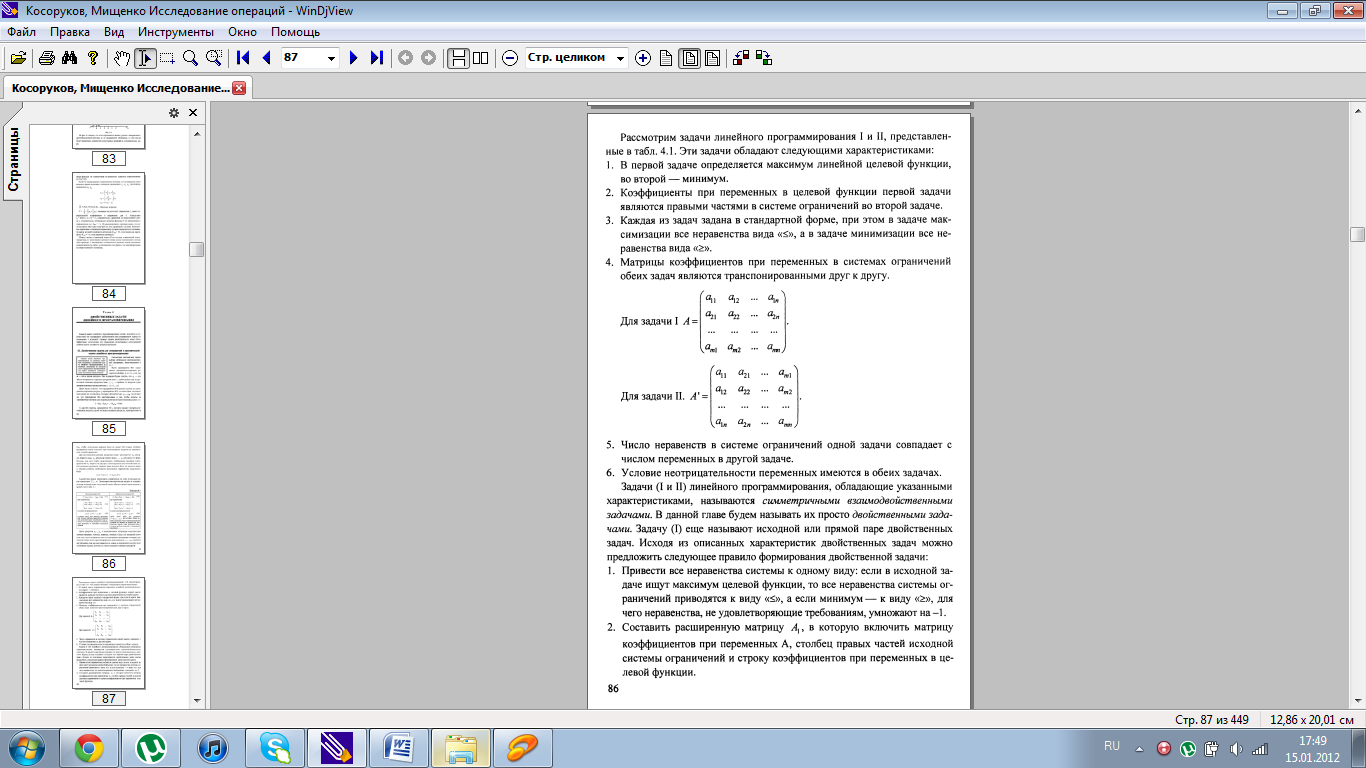
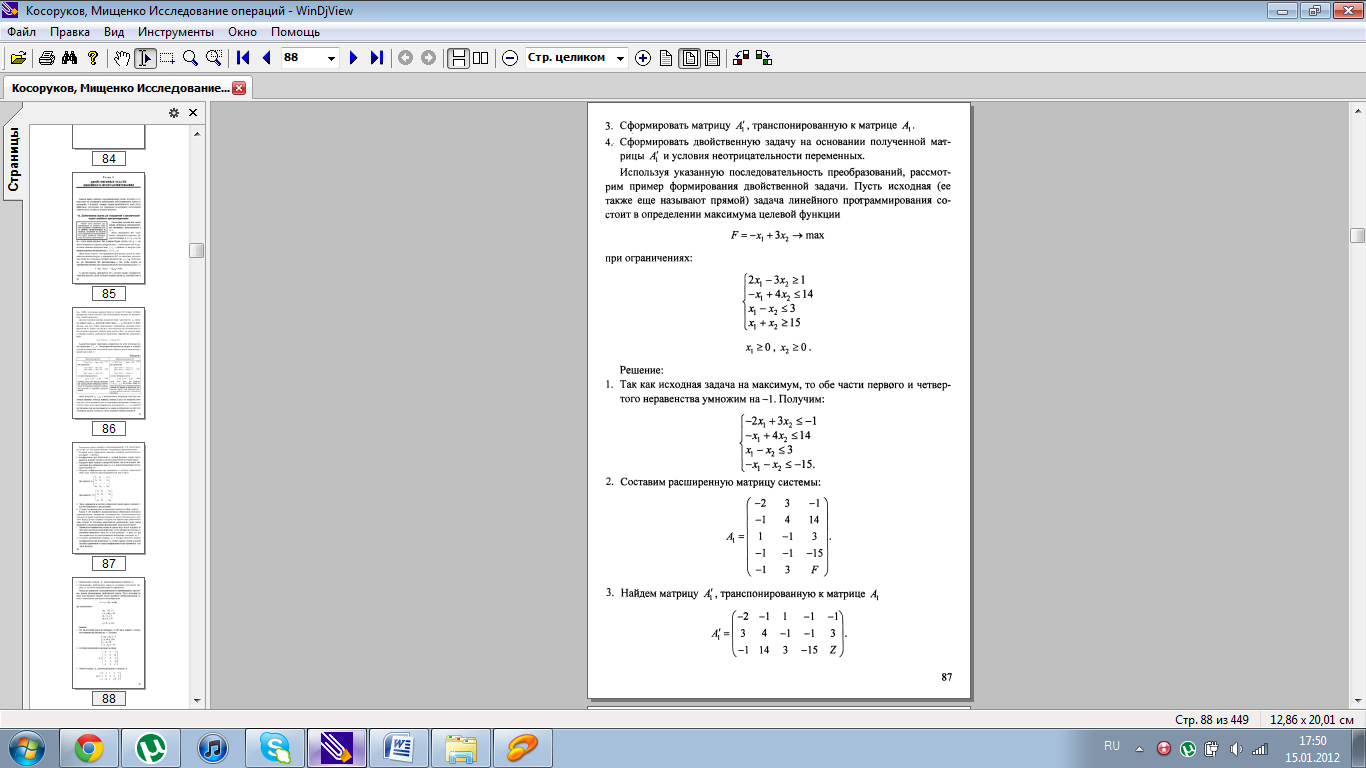
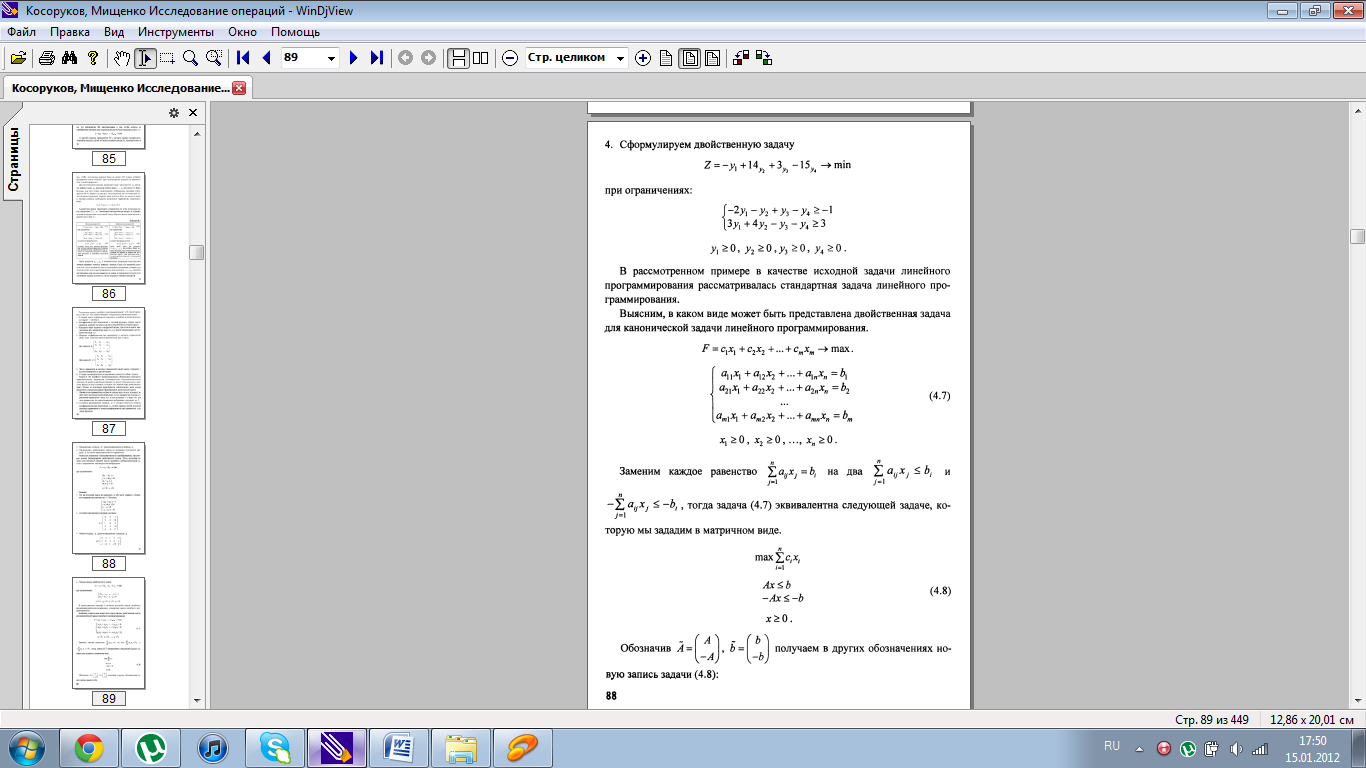
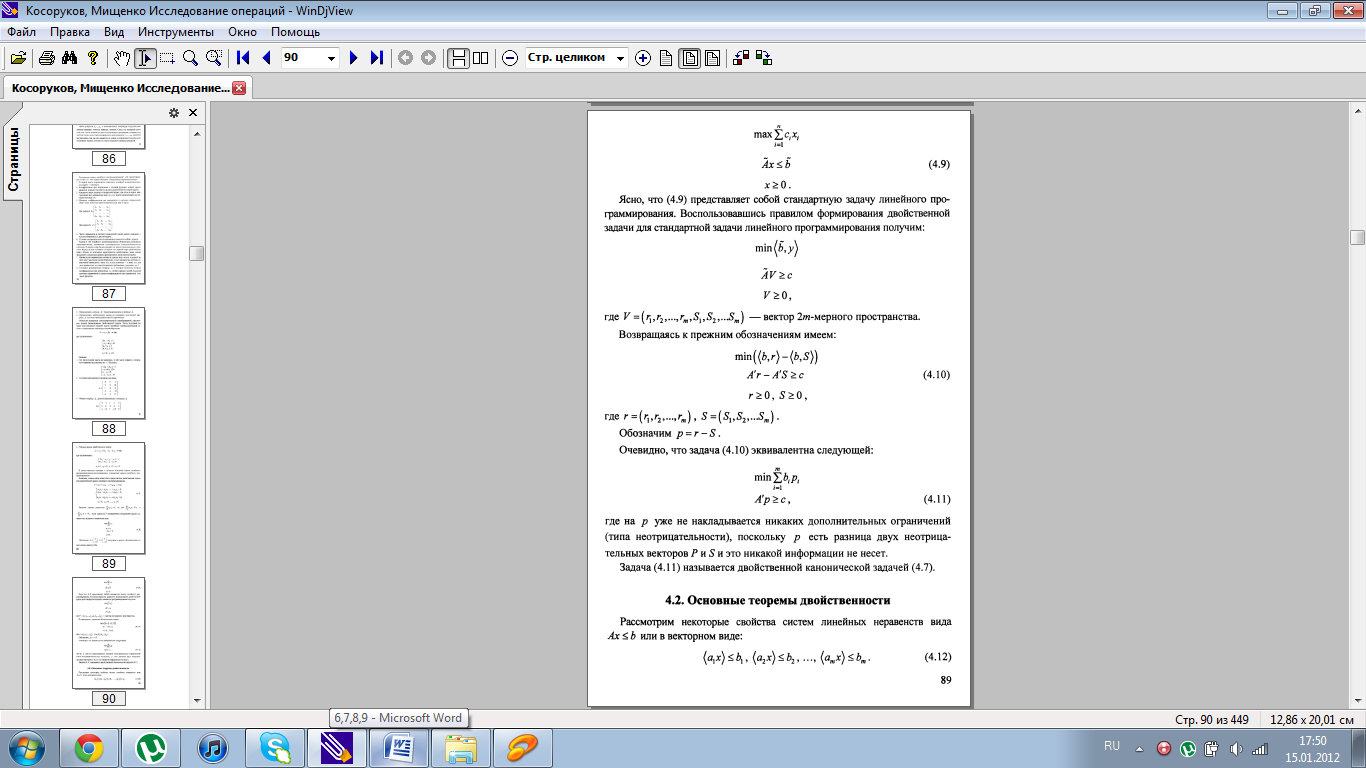
10.Двойственная задача ЛП. Основные теоремы теории двойственности для задач линейного программирования.

Двойственная задача лп

Таблица 4.1

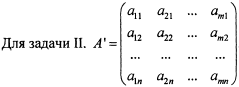
Основные теоремы теории двойственности для задач линейного программирования

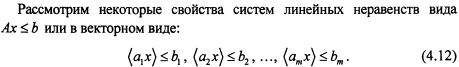
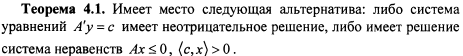
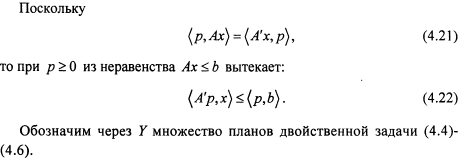
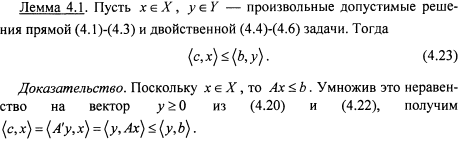
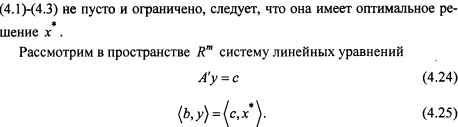
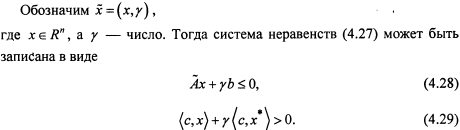
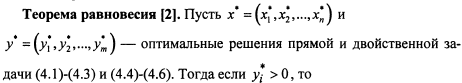
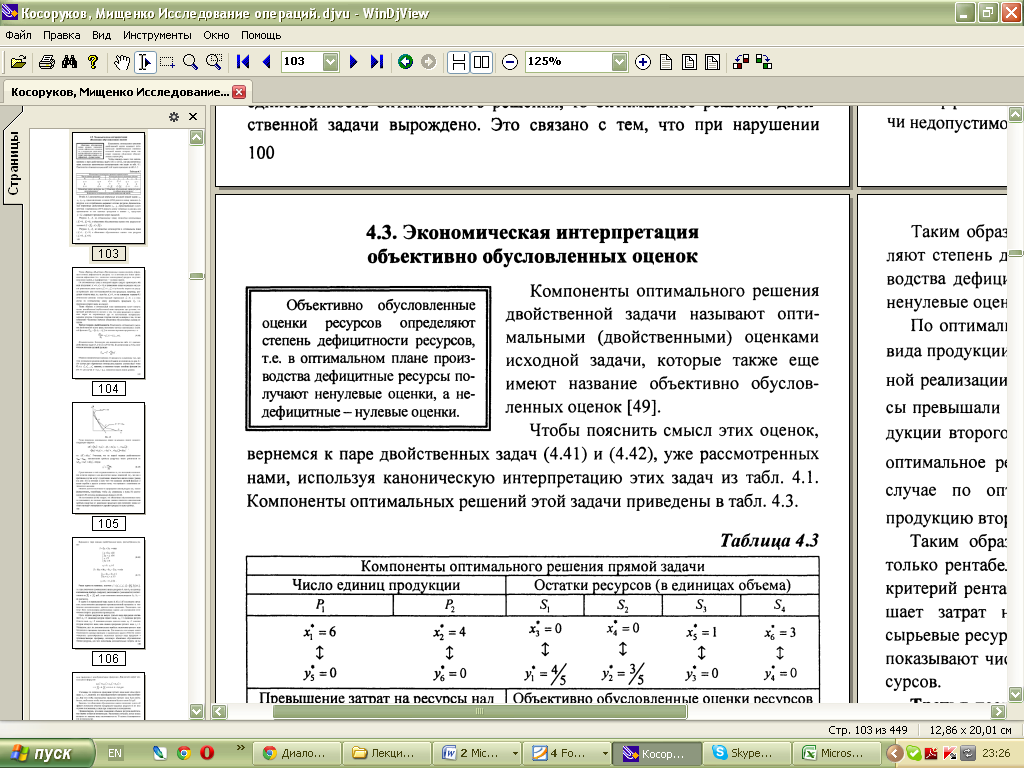
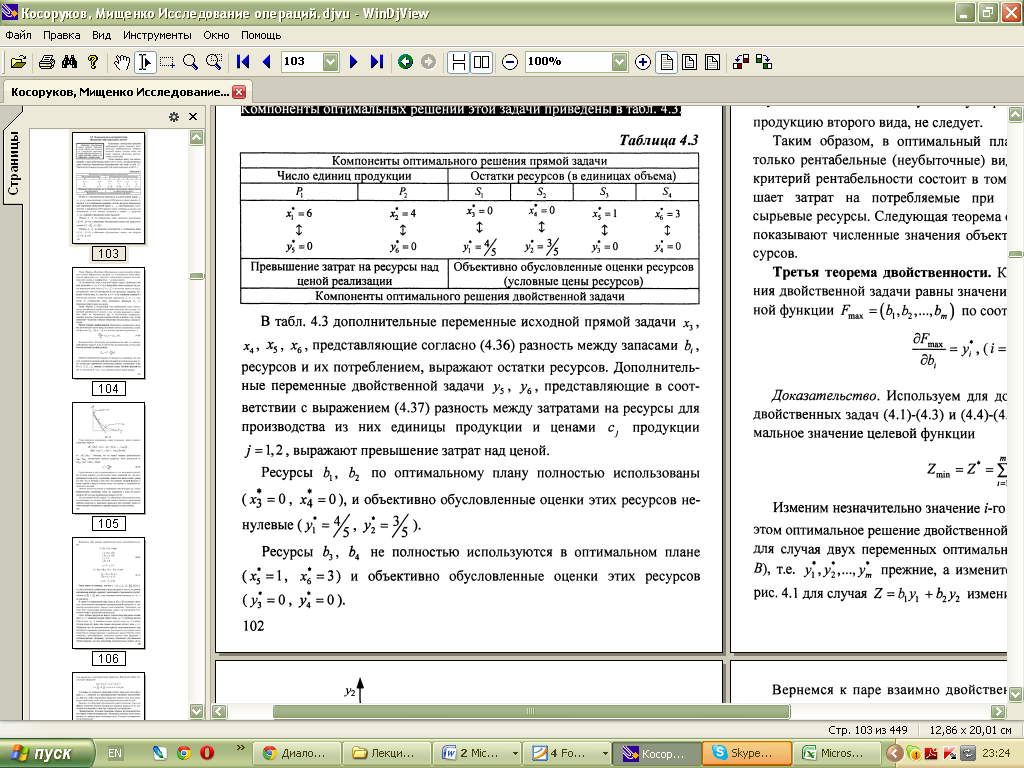
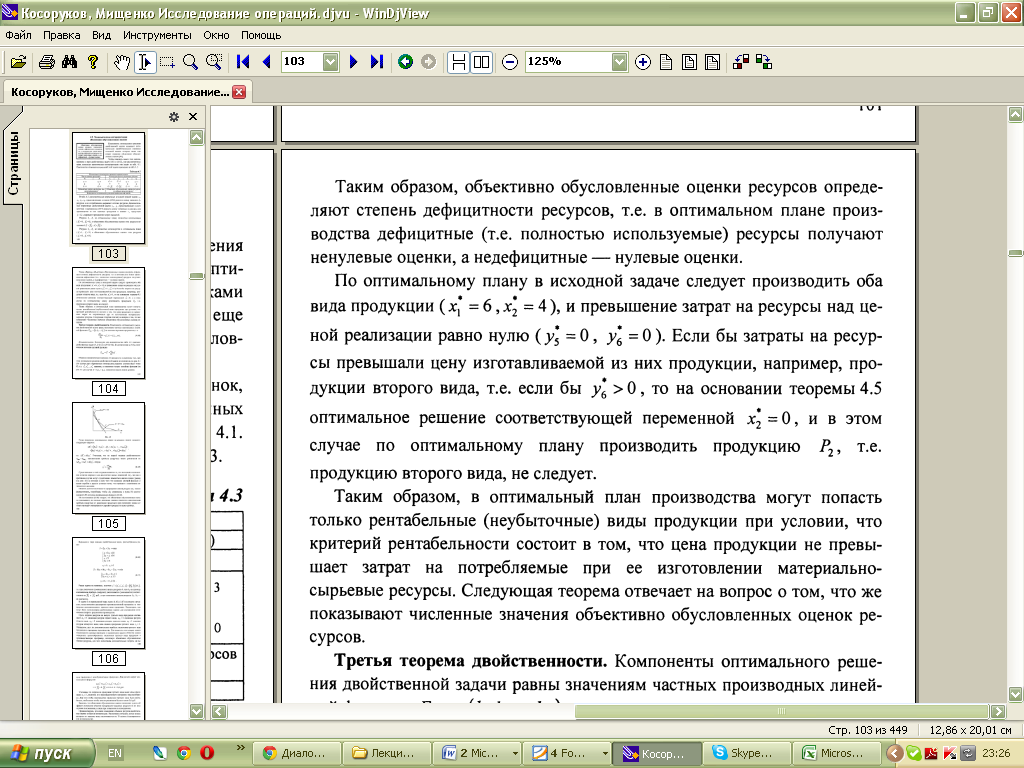
11. Интерпретация двойственных переменных. Теорема Гейла

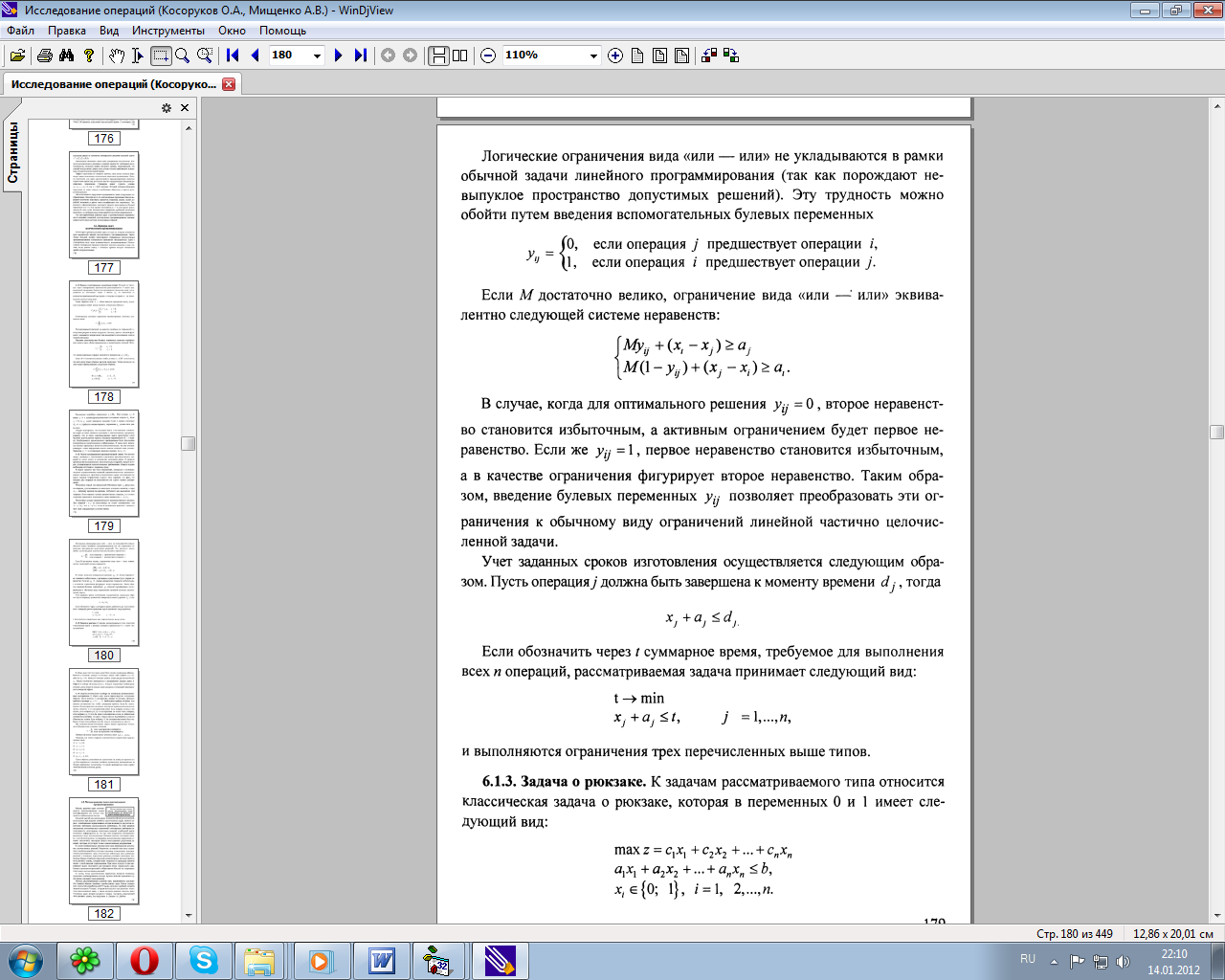
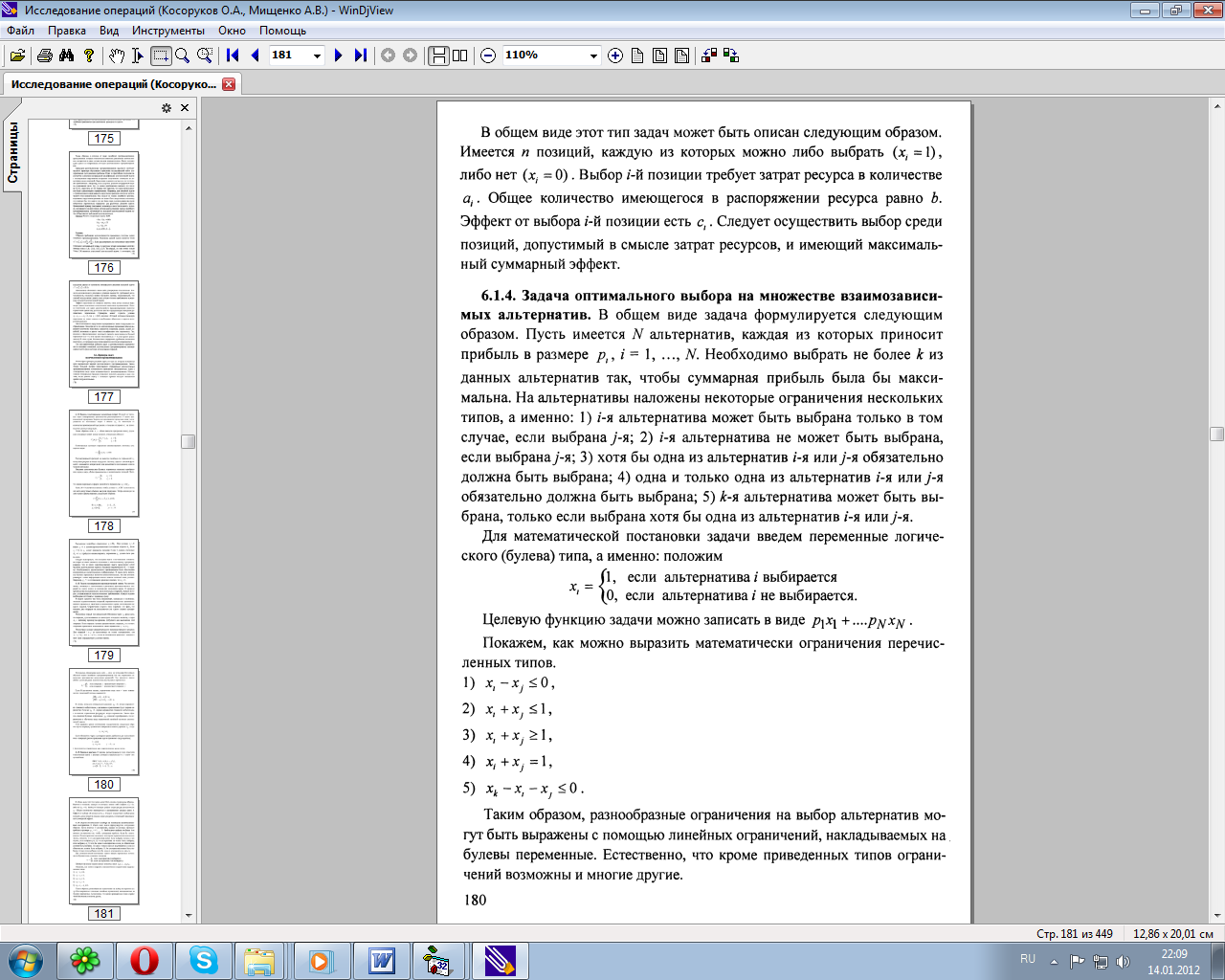
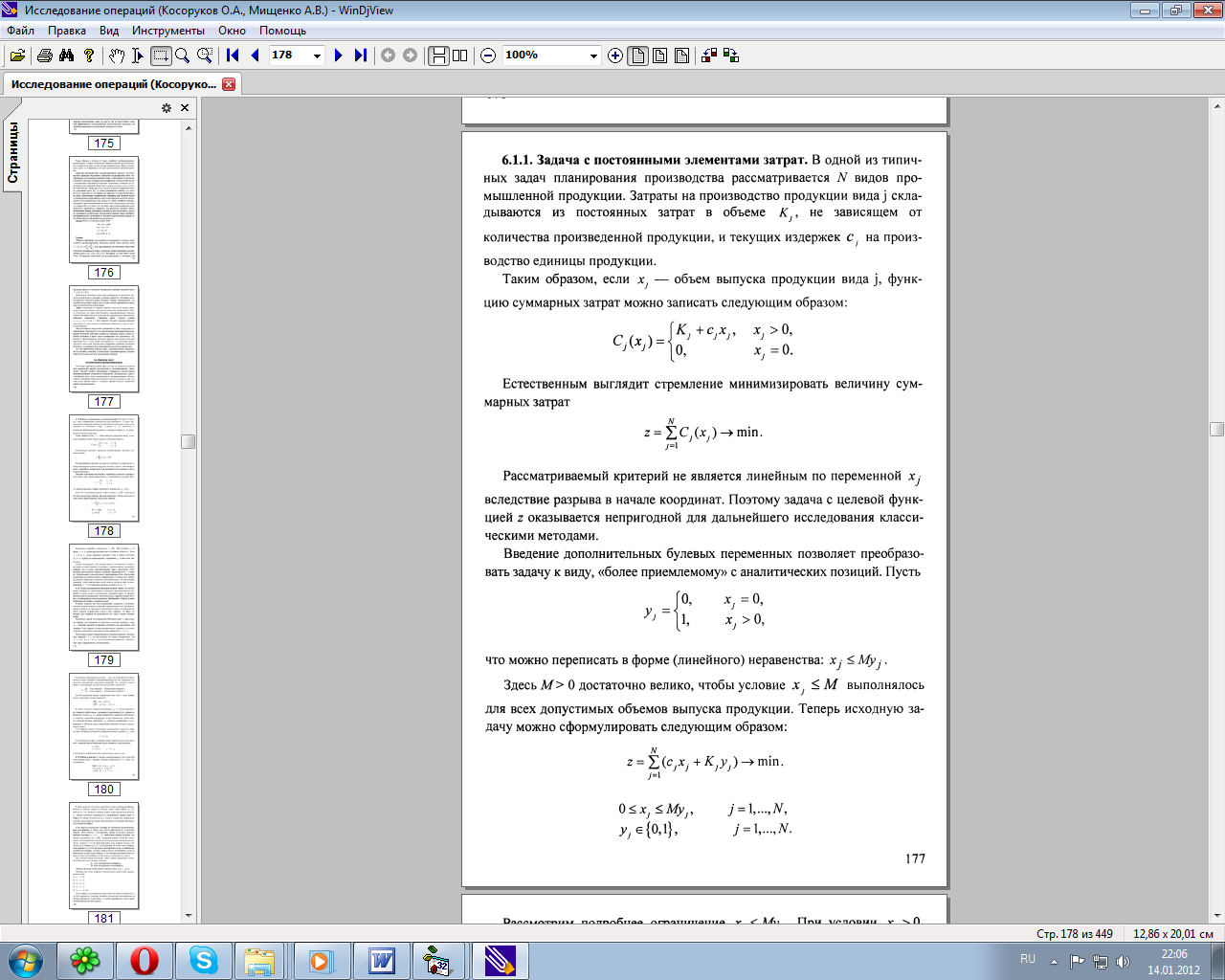
12.Понятия и примеры целочисленных задач линейного программирования (задача "о рюкзаке", задача выбора на множестве взаимозависимых альтернатив, задача производственного планирования с элементами производственных затрат, задача оптимальной диспетчеризации работ на одном станке).

13. Общая идея методов отсечения, метод отсекающих плоскостей Гомори

Требования к отсечению:

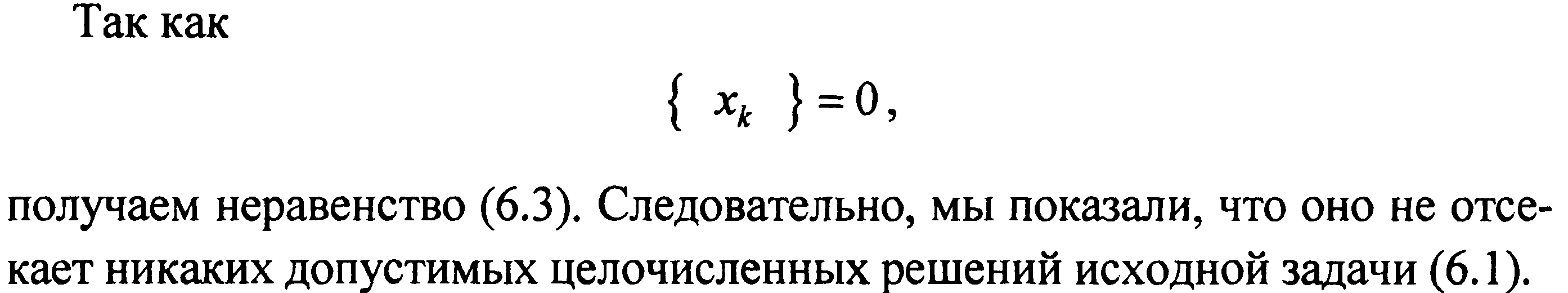
Этапы решения задачи целочисленного линейного программирования методом Гомори:

14. Общая схема методов ветвей и границ

15. Метод ветвей и границ для решения целочисленных задач линейного программирования.

Алгоритм решения задачи ЦЛП:

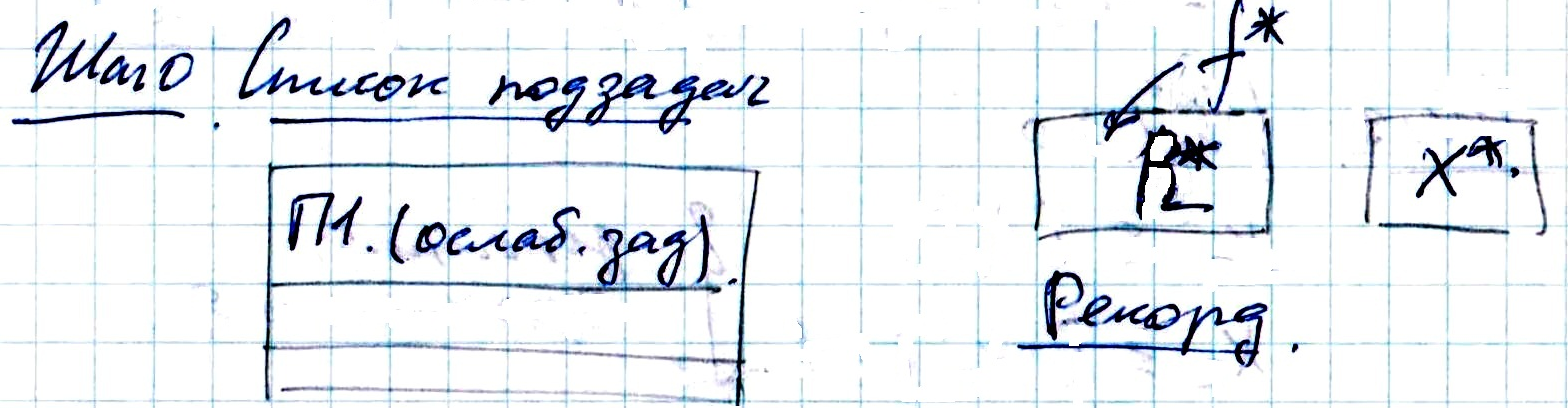
16.Стандартная транспортная задача. Транспортная задача, как задача ЛП. Критерий линейной независимости столбцов матрицы ограничений.

17.Критерий базисного решения для допустимого решения СТЗ. Критерий невырожденности опорного плана СТЗ. Критерий невырожденности СТЗ.

18. Метод «северо-западного угла» нахождения начального опорного плана СТЗ. Метод потенциалов решения СТЗ.

Ai – мощности i-ого поставщика i=1..n

Bj – мощности j-ого потребителя j=1..m

сij – удельные затраты

хij ­– план перевозок

Ограничения для поставщиков:

Метод северо-западного угла

На каждом шаге метода северо-западного угла из всех не вычеркнутых клеток выбирается самая левая и верхняя (северо-западная) клетка. Другими словами, на каждом шаге выбирается первая из оставшихся не вычеркнутых строк и первый из оставшихся не вычеркнутых столбцов.

Для того, чтобы заполнить клетку (i,j), необходимо сравнить текущий запас товара в рассматриваемой i-й строке   с текущей потребностью в рассматриваемом j-м столбце  .

Если существующий запас позволяет перевезти всю потребность, то

·        в клетку (i,j) в качестве перевозки вписывается значение потребности  ;

·        j-й столбец вычеркивается, поскольку его потребность уже исчерпана;

·        от существующего запаса в i-й строке отнимается величина сделанной перевозки, прежний запас зачеркивается, а вместо него записывается остаток, т.е.  .

Если существующий запас не позволяет перевезти всю потребность, то

·        в клетку (i,j) в качестве перевозки вписывается значение запаса  ;

·        i-я строка вычеркивается, поскольку ее запас уже исчерпан;

·        от существующей потребности в j-й строке отнимается величина сделанной перевозки, прежняя потребность зачеркивается, а вместо нее записывается остаток, т.е. .

Нахождение опорного плана продолжается до тех пор, пока не будут вычеркнуты все строки и столбцы.

Пример (из семинара по моделированию):

Ai\Bj	16	18	12	15	11
20	16 ^2	4^3	^9	^7	^0
16	^3	14^4	2^6	^1	^0
14	^5	^1	10^2	4^2	^0
22	^4	^5	^8	11^1	11^0

Маленькие циферки-стоимости перевозок

Метод потенциалов.

Метод потенциалов позволяет определить отправляясь от некоторого опорного плана перевозок построить решение транспортной задачи за конечное число шагов (итераций).       

Общий принцип определения оптимального пла­на транспортной задачи этим методом аналогичен принципу решения задачи линейного программирования симплексным методом, а именно: сначала на­ходят опорный план транспортной задачи, а затем его последовательно улучшают до получения оптимального плана.

Составим двойственную задачу

1.  ,   - любые

2.     

3. 

Пусть есть план  

Теорема (критерий оптимальности): Для того чтобы допустимый план перевозок   в транспортной задаче был оптимальным, необходимо и достаточно, чтобы существовали такие числа  ,   , что

                              если  ,                         (6)

                              если  .                         (7)

числа   и     называются потенциалами пунктов отправления   и назначения   соответственно.

Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем:

Пусть одним из методов найден опорный план. Для этого плана, в ко­тором   базисных клеток, можно определить потенциалы   и   так, чтобы выполнялось условие (6). Один из них задается произвольно (например, приравнивается к нулю). После определяются остальные потенциалы и для каждой из свободных клеток вы­числяются величины  . Если оказалось, что  , то план оп­тимален. Если же хотя бы в одной свободной клетке  , то план не яв­ляется оптимальным и может быть улучшен путем переноса по циклу, соот­ветствующему данной свободной клетке (строим цикл с отправной точкой в этой клетке, в не ставим знак +, а дальше по звеньям чередуем +/-, из всех вершин выбираем минимальное значение, и из всех элементов с “-“ вычитаем его, и прибавляем к элементам с “+”).

Циклом в таблице условий транспортной задачи, называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья - вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое - в столбце. Процесс улучшения плана продолжается до тех пор, пока не будут выполнены условия (7).

19.Постановка задачи транспортного типа со смешанными ограничениями (ЗСО). Сведение ЗСО к задаче о перевозках (ЗП).

20.Сведение ЗП к транспортной задаче с запрещенными перевозками (ТЗП) методом минимальных путей. Сведение ТЗП к стандартной транспортной задаче (СТЗ).

21.Сведение ЗП к транспортной задаче с запрещенными перевозками (ТЗП) методом фиктивных переменных.

22. Основные понятия теории сетевого планирования. Критический путь. Критические работы. Минимальное время наступления события.

В целом сетевые модели делятся на

1. Коммуникационные сети – модели, в которых присутствует понятие потока

2. Сетевые графики – модели, которые отражают выполнение комплексов работ

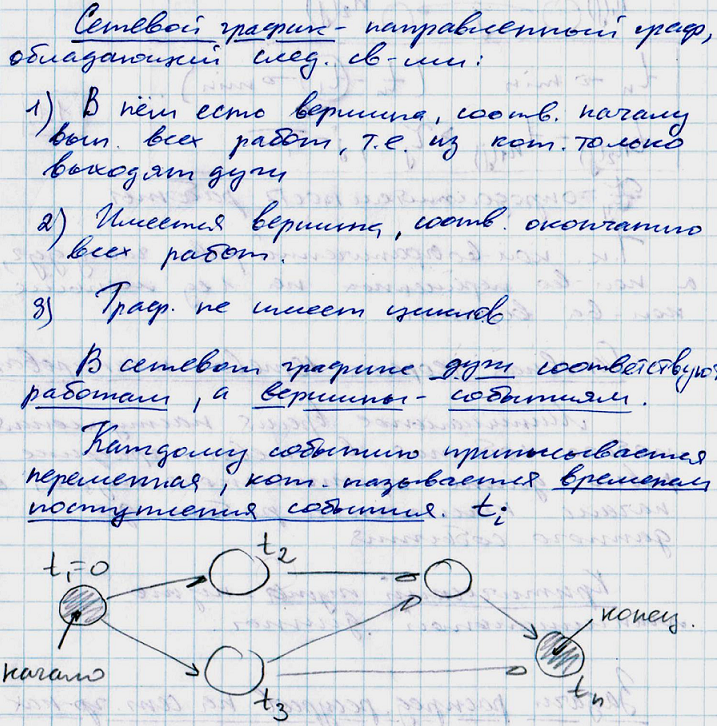
Все события и работы критического пути также называются критическими.

23.Модели распределения ресурсов на сетях и сетевых графиках с учетом неопределенных факторов и риска.

Оптимальное распределение рес-в на сетевых графиках при наличии неопред-ых ф-в

Задача распределения ресурсов на транспорт-х сетях при наличии неопределенных ф-в

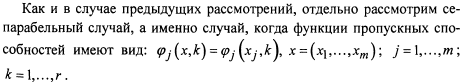
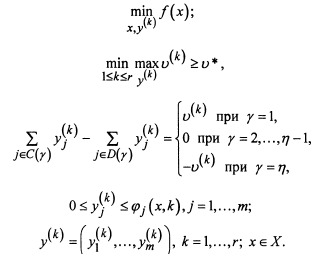
24. Метод динамического программирования (МДП) (основные элементы и схема решения, примеры задач)

Это некоторый подход к решению оптимизационных задач.

Важный отличительный признак МДП: решение задач от конца к началу.

Основные моменты и схема решения

1. Выделяют конечное число последовательных этапов.

2. На каждом этапе выделяется некоторое количество состояний

3. Необходимо определить, чем характеризуются состояния.

4. Определяем множество возможных переходов (из каких состояний можно перейти в какие). Эти этапы и состояния определены таким образом, что переходы возможны только в последующую группу состояний.

5. Определяем «стоимости» переходов (для этого необх. найти маршрут, кот минимизирует интегральную «стоимость» по всем переходам.

Примеры задач