
- •Линейные одномерные системы автоматического управления
- •Линейные одномерные системы автоматического управления
- •Теория автоматического управления
- •Введение
- •Глава 1. Уравнения, элементарные блоки, структурные схемы и переходные процессы в сау
- •. Уравнения сау
- •1.2. Передаточные функции
- •1.3. Переходная и импульсная переходная функции. Показатели качества переходного процесса
- •1.4. Элементарные звенья
- •1.5. Структурные схемы сау и правила их преобразования
- •Глава 2. Обоснование метода передаточных функций для исследования сау
- •2.1. Преобразование Лапласа
- •2.2. Основные теоремы операционного исчисления
- •2.3. Реакция сау на произвольное входное воздействие. Интеграл Дюамеля
- •Глава 3. Частотные характеристики сау
- •3.1. Амплитудно-фазовые частотные характеристики
- •Логарифмические частотные характеристики
- •3.3. Частотные характеристики элементарных звеньев
- •Глава 4. Устойчивость сау
- •Алгебраический критерий устойчивости Гурвица.
- •4.2. Частотный критерий устойчивости Михайлова.
- •4.3. Частотный критерий устойчивости Найквиста
- •4.3.1. Критерий асимптотической устойчивости замкнутой системы, содержащей лишь устойчивые звенья
- •4.3.2. Применение критерия Найквиста к системам с нейтральными звеньями
- •4.3.3 Применение критерия Найквиста к системам с неустойчивыми звеньями
- •4.4 Метод d – разбиения
- •4.4.1 Линейная зависимость коэффициентов характеристического уравнения от одного параметра
- •4.4.2 Линейная зависимость коэффициентов характеристического уравнения от двух параметров
- •Приложение 1. Задачи
- •1. Динамические и частотные характеристики сау
- •Литература
4.4 Метод d – разбиения
Рассмотрим САУ, у
которой коэффициенты характеристического
полинома
зависят
от некоторого набора параметров {![]() }
}
![]() .
.
Каждой точке
пространства параметров {
}
соответствует набор коэффициентов
![]() и
какие-то корни характеристического
уравнения
и
какие-то корни характеристического
уравнения
.
Пусть
корней уравнения находятся в правой
полуплоскости, тогда
![]() корней этого уравнения – в левой
полуплоскости. Совокупность точек в
пространстве {
}
таких, что
корней уравнения находятся в правой
полуплоскости а(
)
корней – в левой, обозначим через
корней этого уравнения – в левой
полуплоскости. Совокупность точек в
пространстве {
}
таких, что
корней уравнения находятся в правой
полуплоскости а(
)
корней – в левой, обозначим через
![]() ,
заметим, что область
,
заметим, что область
![]() представляет собой область устойчивости
САУ в пространстве параметров {
}
представляет собой область устойчивости
САУ в пространстве параметров {
}
При движении точки
в пространстве {
}
внутри какой либо области
не изменяется количество корней в левой
и правой полуплоскостях. Как только
один из корней характеристического
уравнения попадает на мнимую ось (т.е.
![]() ),
соответствующая точка в пространстве
параметров {
}
выходит на границу области D
– разбиения
),
соответствующая точка в пространстве
параметров {
}
выходит на границу области D
– разбиения
![]()
Приравнивая к нулю отдельно действительную и мнимую части уравнения , получим границу области D – разбиения в параметрическом виде.

4.4.1 Линейная зависимость коэффициентов характеристического уравнения от одного параметра
Предположим, что
коэффициенты характеристического
уравнения Линейным образом зависят
от параметра
![]() :
:
![]() ;
;
![]()
В этом случае граница области D-разбиения принимает вид
![]() ,
,
откуда находим
![]() .
.
Заметим, что функция
![]() комплексная,
хотя исходный параметр
был вещественным. Поэтому, после
построения области устойчивости на
комплексной плоскости (
комплексная,
хотя исходный параметр
был вещественным. Поэтому, после
построения области устойчивости на
комплексной плоскости (![]() )
выделяют только вещественные значения
параметра
.
)
выделяют только вещественные значения
параметра
.
Кривая
на комплексной плоскости (
)
представляет собой образ мнимой оси
,
![]() на плоскости
.
Если заштриховать мнимую ось слева, то
при изменении
от
до
кривая
также
будет заштрихована слева. При этом, если
параметр
,
пересекая границу области D
– разбиения, переходит из заштрихованной
стороны в не заштрихованную, то
соответственно корень характеристического
уравнения переходит из левой
полуплоскости в правую.
на плоскости
.
Если заштриховать мнимую ось слева, то
при изменении
от
до
кривая
также
будет заштрихована слева. При этом, если
параметр
,
пересекая границу области D
– разбиения, переходит из заштрихованной
стороны в не заштрихованную, то
соответственно корень характеристического
уравнения переходит из левой
полуплоскости в правую.
Таким образом, построив границу D – разбиения в соответствии с и нанеся штриховку, определяют область – претендент на область устойчивости. Затем внутри такой области выбирают любую точку и проверяют устойчивость САУ, например, с помощью критерия Гурвица. После этого делают окончательный вывод о расположении области устойчивости в пространстве параметров.
4.4.2 Линейная зависимость коэффициентов характеристического уравнения от двух параметров
Предположим что
коэффициенты характеристического
уравнения зависят от двух параметров
![]() :
:
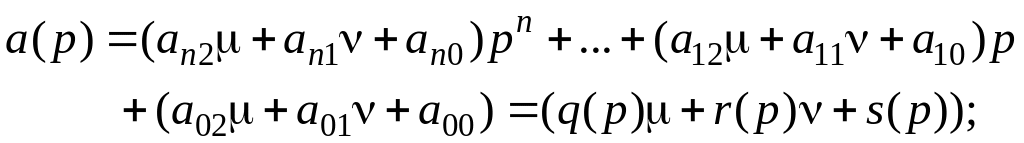

В этом случае граница области D –разбиения принимает вид
![]() ;
;

Откуда разделяя вещественную и мнимую части, находим:

Введем следующие обозначения

И перепишем решение двух линейных уравнений в виде
![]()
Уравнения задают границу области D – разбиения в параметрическом виде.
Отметим, что
имеют смысл при
![]() .
Если
.
Если
![]() и система несовместна, то такие
и система несовместна, то такие
![]() следует исключить из рассмотрения. Если
следует исключить из рассмотрения. Если
![]() и
система совместна, то вместо двух
уравнений имеем одно уравнение прямой
в плоскости (
).
и
система совместна, то вместо двух
уравнений имеем одно уравнение прямой
в плоскости (
).
![]() .
.
Прямая называется
особой прямой и соответствует корню
![]() уравнения
уравнения
![]() .
Особые прямые также наносятся на
D-разбиение.
.
Особые прямые также наносятся на
D-разбиение.
Если коэффициент
![]() при старшей степени характеристического
уравнения зависит от параметров
,
то на D-разбиение наносится
прямая
при старшей степени характеристического
уравнения зависит от параметров
,
то на D-разбиение наносится
прямая
![]() ,
,
которая также
называется особой прямой. Поясним
сказанное следующим простым примером:
корень характеристического уравнения
![]() равен
равен
![]() и при изменении знака
вблизи нуля этот корень скачком переходит
из
в
или наоборот.
и при изменении знака
вблизи нуля этот корень скачком переходит
из
в
или наоборот.
Правила штриховки кривых D-разбиения и особых прямых. Перечисленные ниже правила штриховки считаются наиболее трудно формализуемым местом в алгоритме построения области устойчивости методом D-разбиения. В каждом конкретном случае необходимо тщательно исследовать полученные на плоскости параметров ( ) области выбирая в них несколько разных точек, определяя с помощью пакета “MatLab” корни характеристического уравнения
Кривая D-разбиения при изменении от до заштриховывается слева, если
 и справа – если
и справа – если
 ;
при этом одна сторона D-разбиения может
быть заштрихована дважды.
;
при этом одна сторона D-разбиения может
быть заштрихована дважды.Особая прямая подвергается штриховке, если при переходе через меняется знак
 ,
т.е.
,
т.е.
 .
.
При этом, если
![]() штриховка однократная; если
штриховка однократная; если
![]() ,
то штриховка двойная. Если при переходе
через
,
то штриховка двойная. Если при переходе
через
![]() знак
не меняется, то особая прямая не
заштриховывается.
знак
не меняется, то особая прямая не
заштриховывается.
Особая прямая подвергается однократной штриховке.
Штриховка особых прямых должна быть согласована со штриховкой кривых D-разбиения так, чтобы внутренние стороны углов в точках стыка оказались заштрихованными (Рис. 4.8).
|
Рис 4.8 Правила штриховки кривых D-разбиения |

