4.2. Частотный критерий устойчивости Михайлова.

В этом и следующем разделах будут изложены методы исследования устойчивости САУ по их частотным характеристикам.

Рис. 4.1 Принцип аргумента

Принцип аргумента. Рассмотрим плоскость комплексного переменного p, на которой выберем точки соответственно в левой и правой полуплоскости (Рис. 4.1). Выберем на мнимой оси точку и рассмотрим комплексные векторы . При изменении от до векторы поворачиваются соответственно на углы .

Рассмотрим САУ с передаточной функцией и исследуем устойчивость ее характеристического полинома

Построим годограф комплексного вектора при изменении частоты от до . Обозначим это приращение через

Согласно основной теореме алгебры, имеем:

,где корни уравнения ; поэтому

пусть l корней уравнения расположены в правой полуплоскости, а - в левой полуплоскости. Тогда из следует, что

Формула представляет собой принцип аргумента.

Назовем характеристической кривой или кривой Михайлова годограф комплексного вектора при изменении от до . Имеем

;

.

Поэтому , т.е. кривая Михайлова симметрична относительно оси абсцисс и ее достаточно построить для . В этом случае принцип аргумента принимает вид

Формулировка критерия Михайлова. САУ с передаточной функцией устойчива тогда и только тогда, когда

где n – степень характеристического полинома .

Рис. 4.2 Примеры кривых Михайлова для устойчивых (слева) и

неустойчивых (справа) САУ.

Замечание. Если САУ с передаточной функцией дополнительно охвачена отрицательной обратной связью, то ее передаточная функция . Поэтому кривая Михайлова в этом случае представляет собой годограф комплексного вектора и критерий Михайлова приобретает вид

.

4.3. Частотный критерий устойчивости Найквиста

Рассмотрим САУ с отрицательной обратной связью, для которой передаточные функции разомкнутого и замкнутого контуров равны соответственно

Приведенный ниже критерий устойчивости позволяет по АФЧХ разомкнутой САУ судить о устойчивости замкнутой САУ. В этом его практическая ценность, так как зачастую легче определить частотные характеристики именно разомкнутой системы.

Рассмотрим дробно-рациональную функцию

Нули этой функции совпадают с нулями характеристического полинома замкнутой САУ, а полюсы являются нулями характеристического полинома разомкнутой САУ.

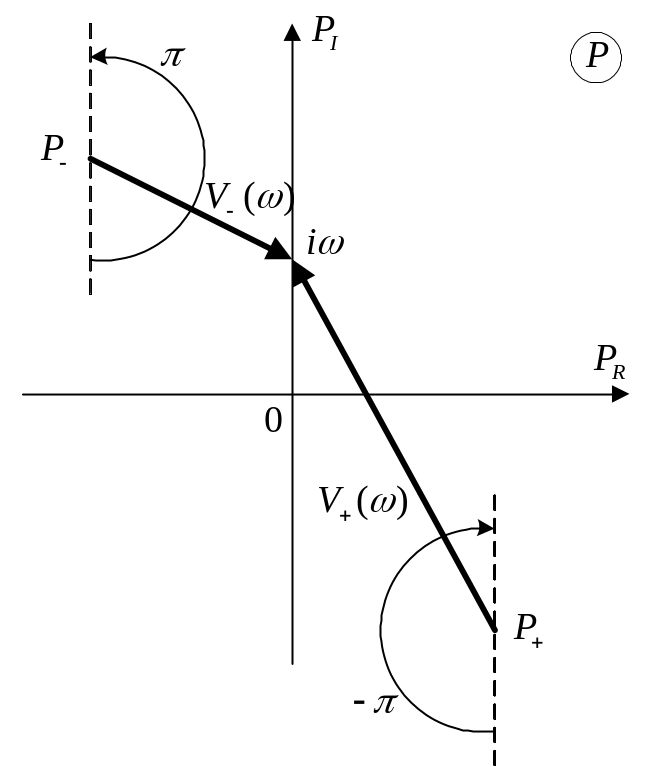
Рис 4.3 Нули и полюсы функции 1+f(p)

На плоскости комплексного переменного p (Рис. 4.3) рассмотрим область, ограниченную контуром G. Обозначим через число нулей и полюсов функции 1+ внутри G. Направление обхода контура G выберем по часовой стрелке. В связи с этим приводимые ниже формулы будут отличаться знаком от известных в литературе, т.к. при вычислении контурных интегралов положительным считается направление против часовой стрелки.

Запишем теорему Коши [2, c.33] для подсчета нулей и полюсов дробно- рациональной функции 1+ комплексного переменного внутри области G

где .

Выполним конформное отображение [7] плоскости p на плоскость по формуле . При этом контур G перейдет в контур Г, а интеграл примет вид

Заметим что направление обхода по контуру Г не задается, а определяется направлением обхода по контуру G и отображением

Рис 4.4 Конформное отображение f=f(p)

На рис. 4.4 приведен пример отображения контура G в плоскости p на контур Г в плоскости f. Контур G представляет собой полуокружность с радиусом R в правой полуплоскости, диаметром которой служит отрезок мнимой оси. Заметим, что при контур G охватывает всю правую полуплоскость, а контур стягивается в точку на оси абсцисс.

Свойства контура Г

1). Поскольку коэффициенты полиномов действительны, то действительным точкам контура G соответствуют действительные точки контура Г; например, точкам соответствуют точки на оси абсцисс. Заметим, что

.

На контуре G_R имеем ( - изменяется от до ).

2). Если сопряженные точки на контуре G, то ; поэтому им соответствуют сопряженные точки на контуре Г. Следовательно симметричному относительно оси абсцисс контуру G соответствует симметричный относительно оси абсцисс контур Г.

3). 1+f представляет собой комплексное число, которое характеризуется радиусом-вектором с началом в точке (-1,0) и концом на контуре Г; при этом контур Г называется годографом вектора 1+f при изменении от до

Посчитаем интеграл в , для этого комплексное число 1+f представим в форме:

,

поэтому

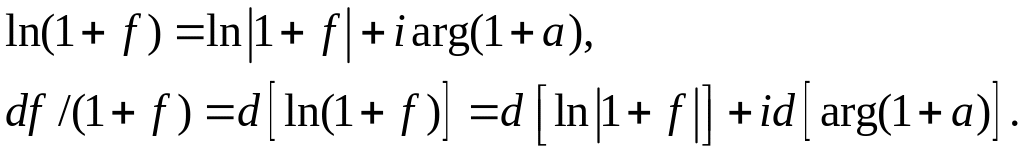
В результате находим

При выводе использован тот факт, что контурный интеграл от дифференциала по замкнутому контуру Г равен нулю, так как начальное и конечное значение модуля вектора совпадают.

Обозначим через число полных оборотов по часовой стрелке вектора , когда p пробегает контур G, а вектор - контур Г. Так как при вычислении контурных интегралов положительным считается направление против часовой стрелки, то

.

Таким образом, из – находим

.

Вывод. Число нулей характеристического полинома замкнутой САУ в правой полуплоскости равно сумме числа нулей характеристического полинома разомкнутой САУ в правой полуплоскости и числа полных оборотов по часовой стрелке годографа вокруг точки (-1,0) при изменении от до .