
- •Глава III. Линейные преобразования
- •3.1. Матрица линейного преобразования
- •3.2. Ядро и образ линейного преобразования
- •3.3. Собственные значения квадратной матрицы
- •1. Найти собственные значения матриц:
- •3.4. Собственные векторы квадратной матрицы
- •3.5. Свойства собственных векторов матрицы
- •3.6. Базис пространства , состоящий из собственных векторов матрицы
- •3.7. Норма линейного преобразования
- •Ортогональные матрицы
- •3.9. Симметрические преобразования и симметрические матрицы
- •Собственные значения симметрической матрицы
- •Собственные векторы симметрической матрицы
3.3. Собственные значения квадратной матрицы
Число
![]() называется собственным
значением
(или характерис-тическим
числом)
квадратной матрицы
порядка
,
если можно подобрать такой n-мерный
ненулевой
вектор
,
что
называется собственным
значением
(или характерис-тическим
числом)
квадратной матрицы
порядка
,
если можно подобрать такой n-мерный
ненулевой
вектор
,
что
![]()
Для того чтобы
найти собственные значения матрицы
,
рассмотрим матрицу
![]()
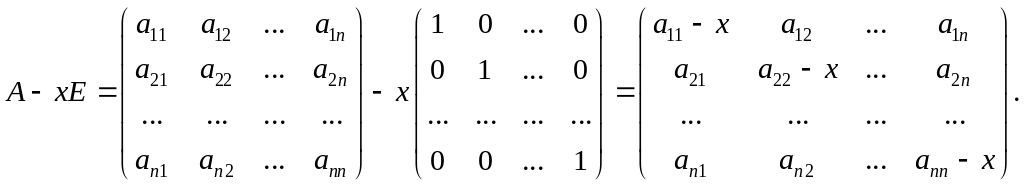
Особый интерес
представляет определитель матрицы
![]() .
Если раскрыть определитель
.
Если раскрыть определитель
![]() ,
то получится многочлен n-й
степени относительно х
,
то получится многочлен n-й
степени относительно х
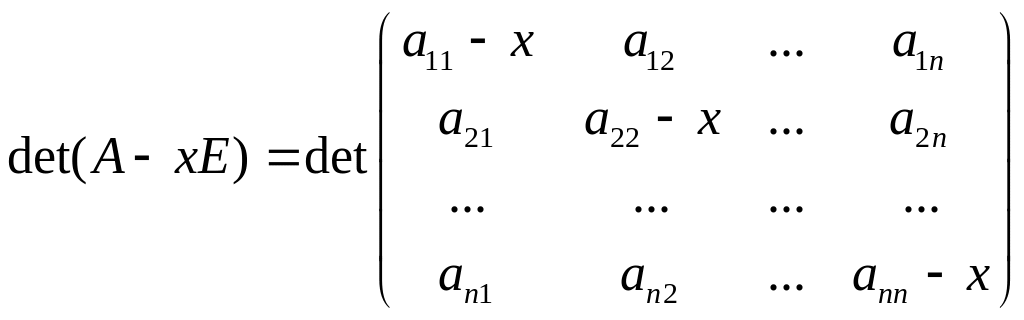
![]()
Этот многочлен
называется характеристическим
многочленом матрицы
.
Его коэффициенты
![]() зависят от элементов матрицы
.
Можно найти выражения для этих
коэффициентов через элементы матрицы
.
Заметим только, что
зависят от элементов матрицы
.
Можно найти выражения для этих
коэффициентов через элементы матрицы
.
Заметим только, что
![]() ,
,
![]() .
.
Уравнение
![]() называется характеристическим
уравнением матрицы
.
называется характеристическим
уравнением матрицы
.
□ Теорема 3.9.
Множество
![]() всех собственных значений матрицы
совпадает с множеством всех решений
характеристического уравнения
матрицы
.
всех собственных значений матрицы
совпадает с множеством всех решений
характеристического уравнения
матрицы
.
Доказательство. Рассмотрим следующую цепочку равносильных утверждений:
![]()
![]()
![]()
![]() уравнения
уравнения
![]() ■
■
Пример
Найти собственные значения матрицы
=
![]()
![]()
![]() .
.
Решение
Сначала найдем характеристический многочлен матрицы .
=![]()
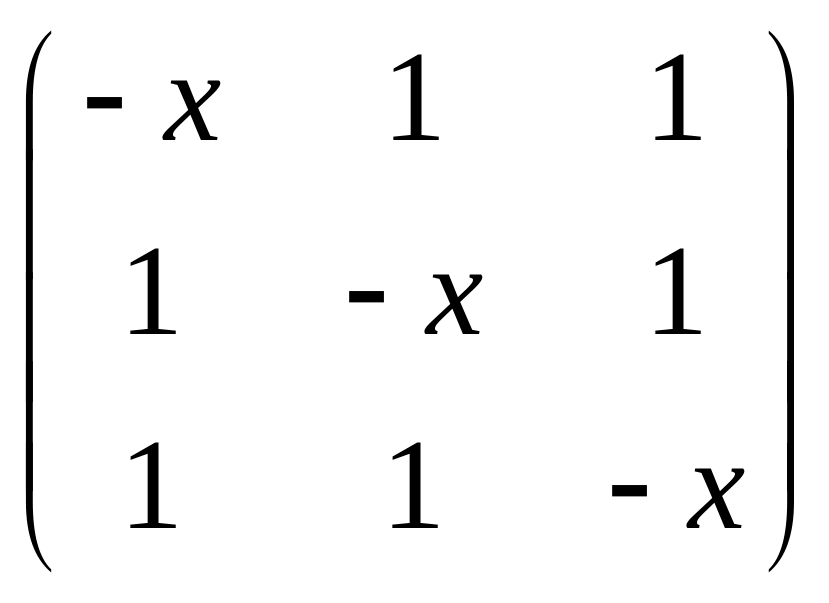
![]() .
.
Собственные
значения матрицы
являются корнями ее характеристического
уравнения
![]() .
Так как
.
Так как
![]()
![]() ,
,
то матрица
имеет два собственных значения:
![]() .
.
Задачи
1. Найти собственные значения матриц:
а)![]() ;
б)
;
б)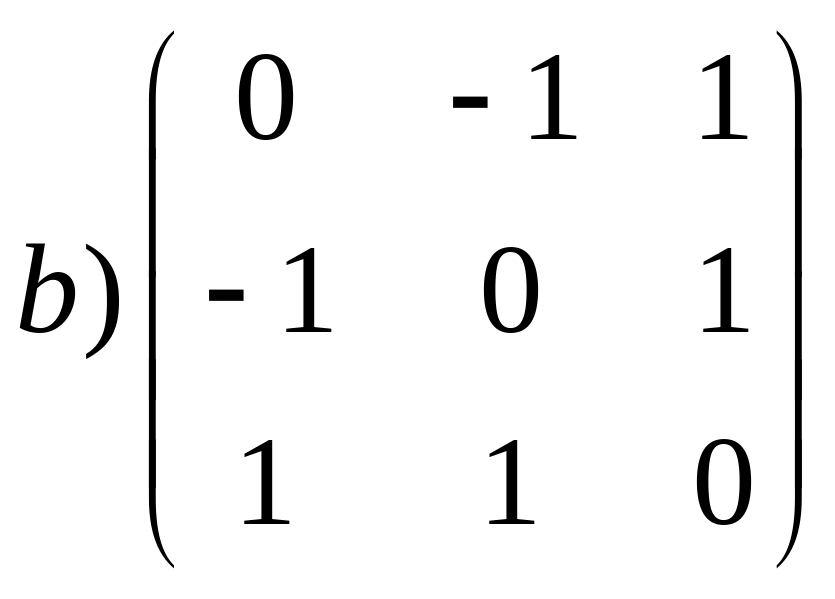 ;
в)
;
в)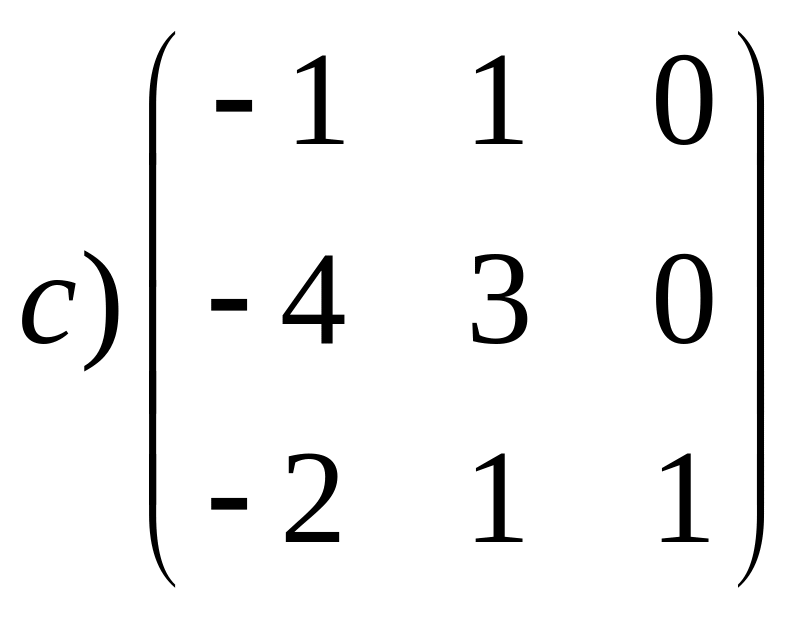 ;
г)
;
г)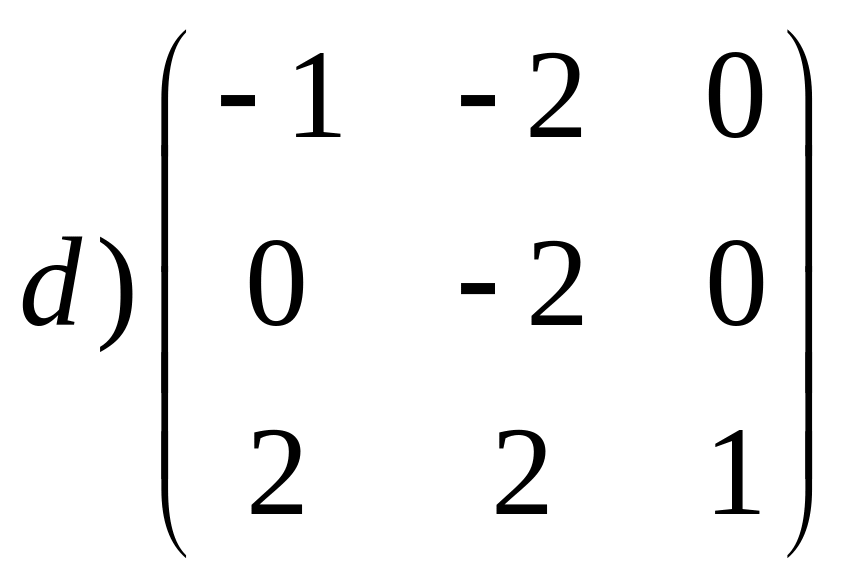 ;
;
д)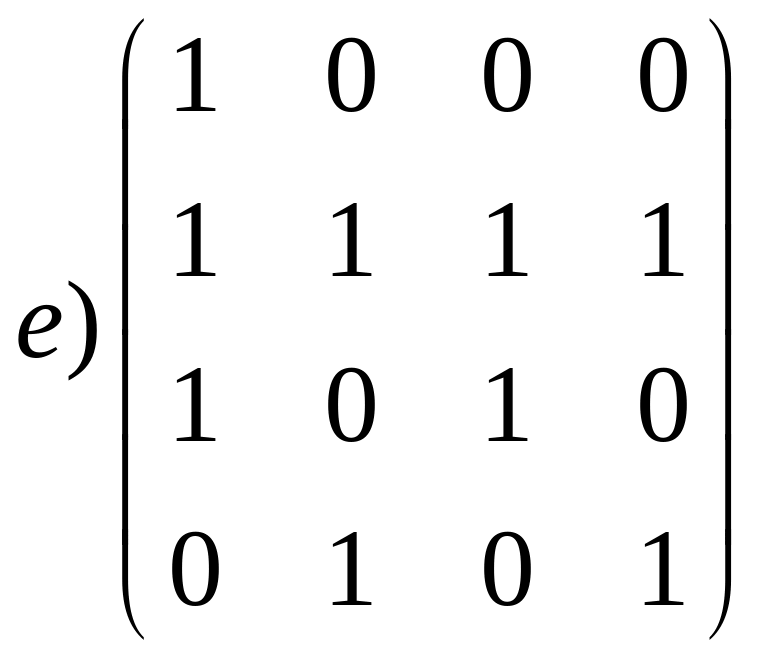 ;
е)f)
;
е)f)
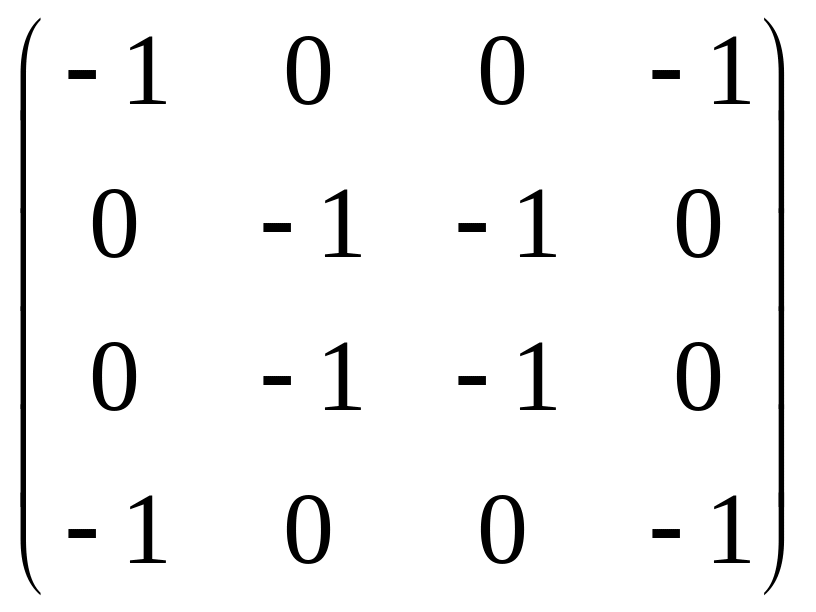 .
.
2. Доказать, что собственные значения диагональной матрицы равны ее диагональным элементам.
3. Найти собственные значения треугольной матрицы.
4. Доказать, что нуль является собственным значением матрицы тогда и только тогда, когда – вырожденная матрица.
5. Доказать, что
собственные значения матрицы
обратные собственным значениям матрицы
![]()
6. Все собственные
значения матрицы
равны
![]() .
Найти все собственные значения матриц:
а)
.
Найти все собственные значения матриц:
а)![]() ;
б)
;
б)
![]()
7. Доказать, что
собственные значения матрицы
и
![]() совпадают, если
– обратимая матрица.
совпадают, если
– обратимая матрица.
8.
Дана матрица
,
квадрат которой совпадает с матрицей
,
т. е.
![]() .
Доказать, что собственные значения
матрицы
равны
.
Доказать, что собственные значения
матрицы
равны
![]() или
или
![]() .
.
9.
Доказать, что собственные значения
матриц
и
![]() совпадают.
совпадают.
3.4. Собственные векторы квадратной матрицы
Собственным
вектором
квадратной матрицы
порядка
,
принадлежащим
ее собственному значению
,
называется n-мерный
вектор
,
для которого
![]() .
.
Множество всех
собственных векторов матрицы
,
принадлежащих ее собственному значению
,
обозначим символом
![]() .
В следующей теореме отыскание собственных
векторов сводится к решению однородной
системы линейных уравнений.
.
В следующей теореме отыскание собственных
векторов сводится к решению однородной
системы линейных уравнений.
□ Теорема 3.10.
Множество
всех собственных векторов матрицы
порядка
,
принадлежащих ее собственному значению
l,
совпадает
с множеством
всех решений однородной системы линейных
уравнений
![]() ,
где
,
где
![]()
Доказательство. Рассмотрим следующую цепочку равносильных утверждений:
![]()
![]()
![]()
![]()
![]() ■
■
Следствие. Множество является подпространством пространства
Так как множество решений однородной системы уравнений является подпространством пространства , то утверждение следствия вытекает из теоремы 3.10.
Теперь сформулируем алгоритм отыскания всех собственных векторов матрицы .
1. Найти все собственные значения матрицы , т. е. найти все корни уравнения =0.
2. Для каждого
![]() ,
,
![]() ,
найти базис подпространства
,
найти базис подпространства
![]() ,
т. е. найти фундаментальный набор решений
системы уравнений
.
,
т. е. найти фундаментальный набор решений
системы уравнений
.
Пример
Найти собственные значения матрицы
![]()
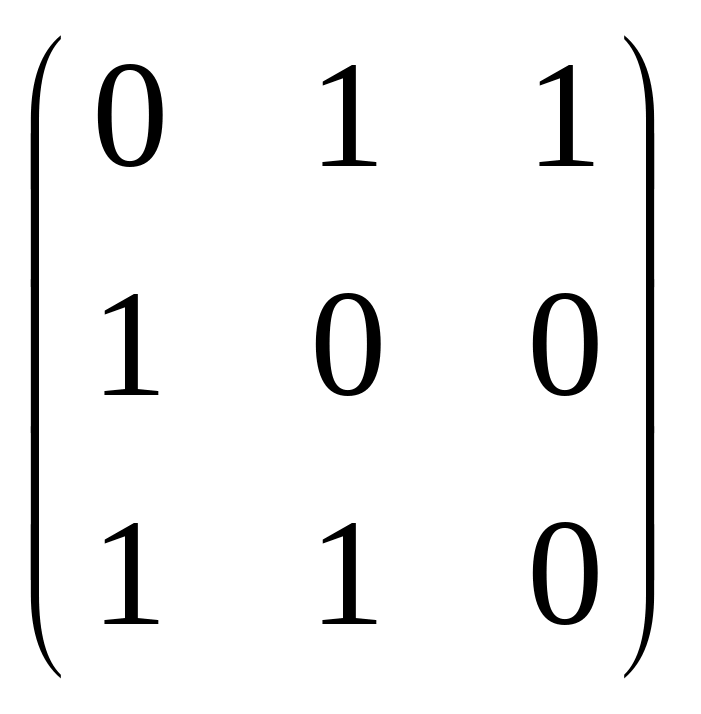 .
.
В примере из п. 3.3
были найдены собственные значения
матрицы
,
а именно
.
Теперь найдем подпространства собственных
векторов
![]() и
и
![]() .
Так как
.
Так как
![]() =
–
=
–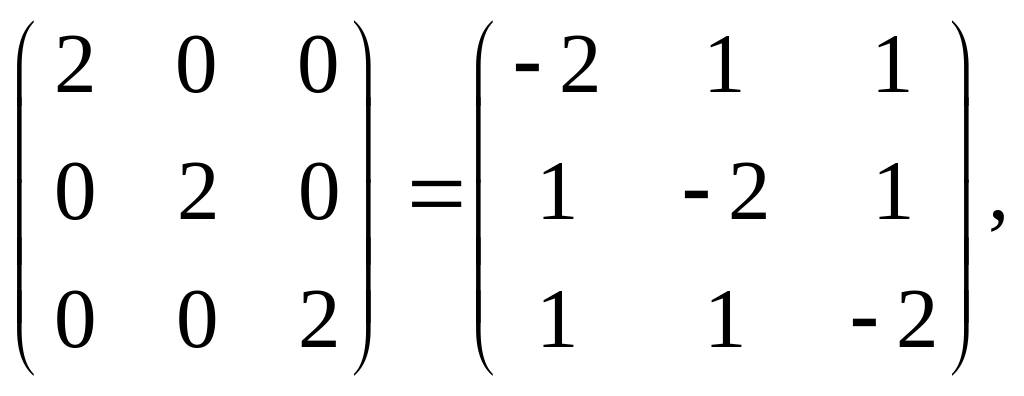
то система линейных
уравнений
![]() имеет следующий вид:
имеет следующий вид:
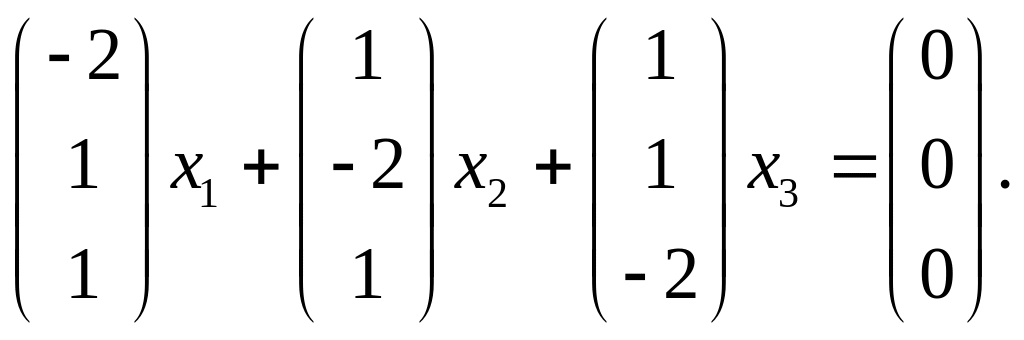
Фундаментальный
набор решений этой системы уравнений
содержит один вектор
![]() который является базисом подпространства
.
который является базисом подпространства
.
Теперь
найдем базис подпространства
.
Построим систему линейных уравнений
![]()

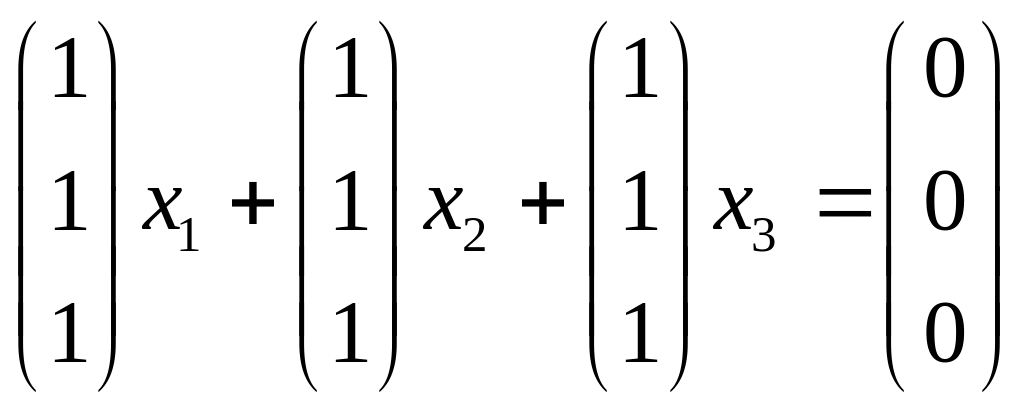 .
.
Фундаментальный
набор решений этой системы уравнений
состоит из векторов
![]() которые образуют базис подпространства
которые образуют базис подпространства
![]()
Задачи
1. Доказать, что матрица порядка имеет единственное собственное значение, если каждый n-мерный вектор является собственным вектором матрицы .
2. Доказать, что все n-мерные векторы тогда и только тогда являются cобственными векторами матрицы , когда матрица имеет вид
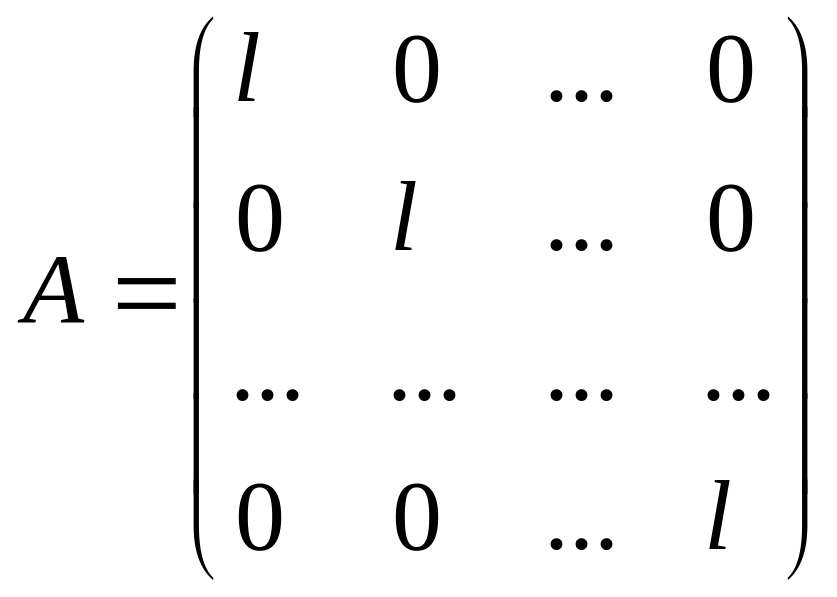
3.
Доказать, что собственные значения
матрицы
и
![]() совпадают. Найти связь между собственными
векторами этих матриц.
совпадают. Найти связь между собственными
векторами этих матриц.
4. Найти собственные векторы матриц
а)![]() ;
б)
;
б)
 ;
в)
;
в)
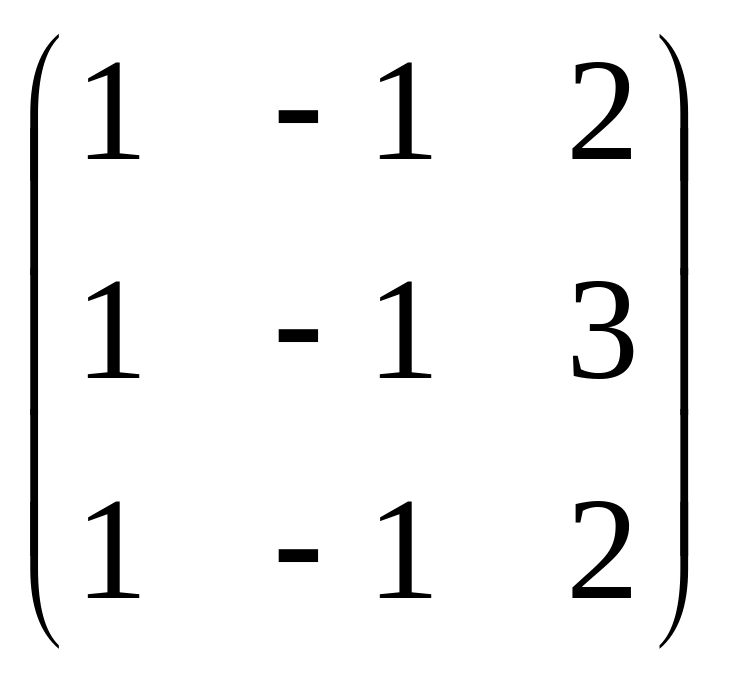 ;
г)
;
г) ;
;
д)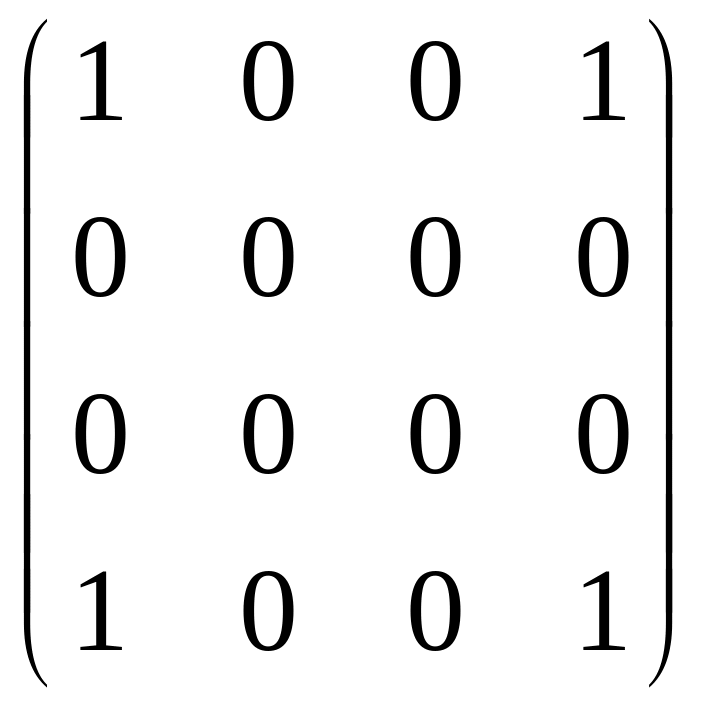 ;
е)
;
е)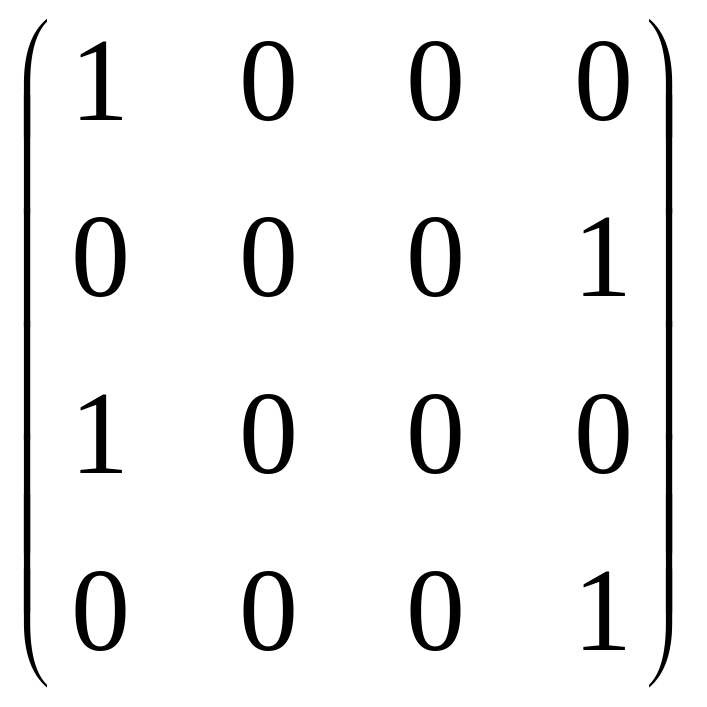 .
.
