
- •Глава III. Линейные преобразования
- •3.1. Матрица линейного преобразования
- •3.2. Ядро и образ линейного преобразования
- •3.3. Собственные значения квадратной матрицы
- •1. Найти собственные значения матриц:
- •3.4. Собственные векторы квадратной матрицы
- •3.5. Свойства собственных векторов матрицы
- •3.6. Базис пространства , состоящий из собственных векторов матрицы
- •3.7. Норма линейного преобразования
- •Ортогональные матрицы
- •3.9. Симметрические преобразования и симметрические матрицы
- •Собственные значения симметрической матрицы
- •Собственные векторы симметрической матрицы
3.7. Норма линейного преобразования
Линейное
преобразование
называется ограниченным
сверху, если
можно подобрать такое число
![]() ,
что для каждого нормированного вектора
,
что для каждого нормированного вектора
![]() из пространства Rn
выполняется неравенство
из пространства Rn
выполняется неравенство
![]()
□ Теорема 3.12. Каждое линейное преобразование пространства ограничено сверху.
Доказательство.
Пусть
![]() − произвольный нормирован-ный вектор
из пространства Rn.
Тогда квадрат длины этого вектора
− произвольный нормирован-ный вектор
из пространства Rn.
Тогда квадрат длины этого вектора
![]() .
.
Отсюда вытекает
![]()
![]() 1,…,
1,…,
![]() 1
+ … +
1
+ … +
![]() .
.
Теперь полагаем
![]() ,
где
,
где
![]() ,
,
и докажем, что
![]()
![]() Действительно,
Действительно,
![]()
![]() ■
■
Из доказанной теоремы следует, что множество
![]()
ограничено сверху.
Следовательно, это множество имеет
точную верхнюю грань, обозначаемую
символом
![]() .
Будем называть ее нормой линейного
преобразования
,
а также называть нормой матрицы
.
Итак,
.
Будем называть ее нормой линейного
преобразования
,
а также называть нормой матрицы
.
Итак,
= Sup{ }
на множестве нормированных векторов пространства Rn.
□ Лемма. Для каждого вектора из пространства Rn справедливо неравенство
![]()
Доказательство.
Если вектор
=
,
то вектор
![]() .
Отсюда
.
Отсюда
![]() и
и
![]() ,
значит утверждение теоремы справедливо.
,
значит утверждение теоремы справедливо.
Если же вектор
![]() ,
то отсюда и из определения нормы линейного
преобразования следует
,
то отсюда и из определения нормы линейного
преобразования следует
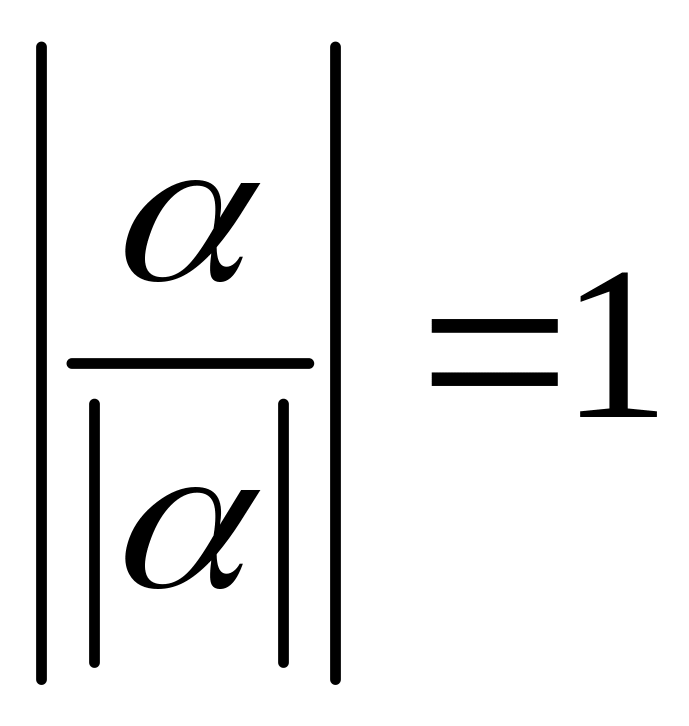
![]()
![]()
![]()
![]()
![]() ■
■
□ Теорема 3.13. Линейное преобразование обратимо тогда и только тогда, когда
![]() {
}
{
}![]()
на множестве нормированных векторов пространства Rn.
Необходимость.
Сначала установим, что норма каждой
обратимой матрицы больше нуля.
Действительно, если длина вектора
равна единице, т. е.
![]() = 1, то
и из обратимости матрицы
следует
= 1, то
и из обратимости матрицы
следует
![]() и, значит,
и, значит,
![]() Теперь, из определения нормы линейного
преобразования имеем
или
Теперь, из определения нормы линейного
преобразования имеем
или
![]()
По условию матрица
обратима, а поэтому обратима матрица
.
Из доказанного выше утверждения следует
![]() > 0. Наконец, если
– произвольный вектор длины единицы,
то, используя лемму, имеем
> 0. Наконец, если
– произвольный вектор длины единицы,
то, используя лемму, имеем
![]()
Отсюда
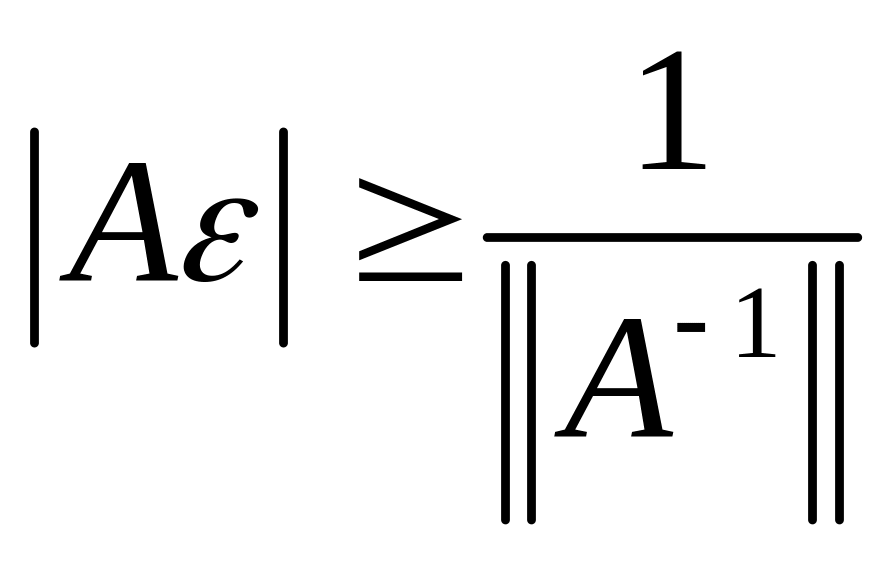 {
}
{
}
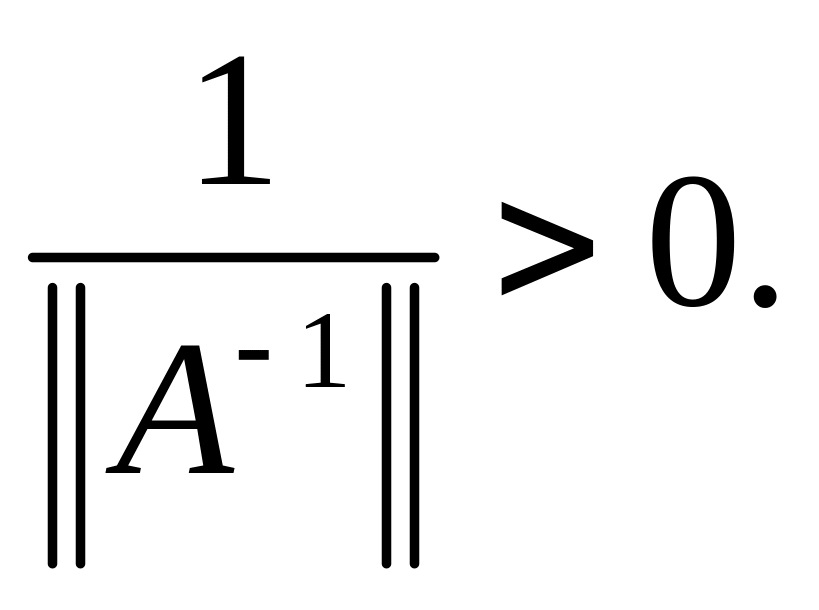
Достаточность.
Дано
{
}
.
Для доказательства обратимости
преобразования
достаточно установить, что
=![]() (теорема 3.6). Предположим противное, т.
е. пусть
.
Это означает, что в подпространстве
найдется ненулевой вектор
(теорема 3.6). Предположим противное, т.
е. пусть
.
Это означает, что в подпространстве
найдется ненулевой вектор
![]() и
.
Теперь рассмотрим следующую цепочку
равенств:
и
.
Теперь рассмотрим следующую цепочку
равенств:
![]() ,
,![]()
 =
=
![]() =
=
![]() =
.
=
.
Итак, нашелся такой нормированный вектор , что = 0. Отсюда вытекает, что
{ } = 0 (13)
на множестве нормированных векторов ε пространства Rn. Равенство (13) противоречит условию достаточности теоремы. ■
Задачи
1. Доказать, что
![]() на множестве нормированных векторов
пространства Rn.
на множестве нормированных векторов
пространства Rn.
2. Найти норму
линейного преобразования
![]() .
.
3. Доказать, что
норма линейного преобразования
равна наибольшему из чисел
![]() ,
,
![]() ,…,
,…,
![]() ,
где
,
где
 .
.
4. Доказать, что норма ненулевой матрицы больше нуля.
5. Доказать, что для любых квадратных матриц и справедливы неравенства:
а)
![]() ;
;
б)
![]() .
.
3.8. Ортогональные преобразования
и ортогональные матрицы
Ортогональные преобразования
Линейное
преобразование
называется ортогональным,
если для каждой пары векторов
![]() из пространства Rn
выполняется равенство
из пространства Rn
выполняется равенство
![]()
Следующая теорема иногда облегчает доказательство ортогональности линейного преобразования.
□ Теорема 3.14. Линейное преобразование будет ортогональным тогда и только тогда, когда выполняются следующие два условия:
1)
![]()
![]() ,
т. е.
преобразование
не изменяет длины векторов;
,
т. е.
преобразование
не изменяет длины векторов;
2)
![]() ,
т. е.
преобразование
не изменяет углы между векторами.
,
т. е.
преобразование
не изменяет углы между векторами.
Необходимость вытекает из следующих равенств:
![]()
![]()
Достаточность. Ортогональность преобразования следует из следующей цепочки равенств:
![]() .
■
.
■
В следующей теореме, характеризующей ортогональные преобразования, содержится, в частности, критерий, которому должны удовлетворять матрицы ортогональных преобразований.
□ Теорема 3.15. Рассмотрим линейное преобразование . Тогда следующие условия равносильны:
1) линейное преобразование ортогонально;
2) линейное
преобразование
переводит ортонормированный базис
пространств Rn
в ортонормированный базис, т. е. если
,…,
– ортонормированный базис, то![]() – ортонормированный базис пространства
Rn;
– ортонормированный базис пространства
Rn;
3) столбцы матрицы образуют ортонормированную систему векторов.
Доказательство
1) 2). Пусть ,…, − ортонормированный базис Rn, т. е.
![]() = 0, если
= 0, если
![]() ,
,
= 1,
![]()
Так как из условия
1) теоремы следует, что
![]() для каждой пары векторов
,
из пространства
Rn,
то
для каждой пары векторов
,
из пространства
Rn,
то
![]() если
,
если
,
![]()
Отсюда вытекает, что является ортонормированной системой векторов и, значит, она линейно независимая. Так как эта система содержит n векторов, то из теоремы 1.5 следует, что базис Rn.
2)
3).
Рассмотрим диагональную систему векторов
![]() ,
которая является ортонормированным
базисом Rn.
Из условия 2) теоремы получаем, что
,
которая является ортонормированным
базисом Rn.
Из условия 2) теоремы получаем, что
![]() ортонормированный базис
Rn.
Так как из определения матрицы линейного
преобразования следует
ортонормированный базис
Rn.
Так как из определения матрицы линейного
преобразования следует
![]() ,
,
![]() то
то
![]() – ортонормированная система векторов.
– ортонормированная система векторов.
3)
1).
Пусть
![]() и
и
![]() –
произвольная пара векторов пространства
Rn.
Тогда
–
произвольная пара векторов пространства
Rn.
Тогда
![]() ,
(14)
,
(14)
![]()
![]() ,
,
![]()
![]() .
.
По условию 3) теоремы, система векторов является ортонормированной. Теперь из свойства 3 [1. §7] ортогональных систем векторов получаем, что
![]() .
(15)
.
(15)
Из сопоставления соотношений (14) и (15) вытекает равенство
![]() ,
,
т. е. ортогональность
линейного преобразования
![]() ■
■
