2.10. Проверка нормальности распределения

При рассмотрении всех предыдущих статистических процедур предполагалось, что выходная величина подчиняется нормальному закону распределения. Это предположение можно проверить разными способами. Наиболее строгим из них является применение критерия Пирсона. Для этого необходимо иметь выборку достаточно большого объема: . Диапазон изменения выходной величины в этой выборке разбивается на интервалов так, чтобы эти интервалы покрывали всю ось от до и в каждый интервал при этом попало не менее пяти значений выходной величины. Подсчитывают количество , наблюдений, попавших в каждый интервал. Затем вычисляют теоретические вероятности попадания случайной величины в каждый интервал. Для этого используют формулу

где

(2.21)

где среднее арифметическое выборки; среднее квадратическое отклонение выборки; нижняя граница го интервала; верхняя граница го интервала; нормированная функция Лапласа:

Значения ее для и определяются из специальных таблиц, которые приведены во многих справочных и учебных пособиях по теории вероятностей и математической статистике. При отыскании значений этой функции для отрицательных аргументов следует иметь ввиду, что функция нечетная:

Для вычисления теоретических вероятностей попадания случайной величины в каждый интервал можно воспользоваться формулой

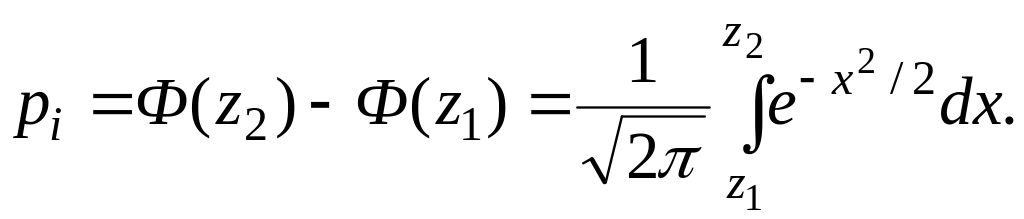
Значения легко получить на персональном компьютере с помощью математического пакета, например фирмы .

Следующим этапом является вычисление величины по формуле

(2.22)

По выбранному уровню значимости и числу степеней свободы из таблиц распределения выбирают величину . Гипотезу о нормальности распределения можно принять, если

Менее строгой и поэтому не часто применяемой является проверка нормальности распределения по критерию Колмогорова.

2.11. Коэффициент корреляции

Во многих случаях целью экспериментальных исследований является установление и изучение зависимости между некоторыми величинами. Если каждая из этих величин является случайной, то при этом используют методы корреляционного анализа. Так, методами корреляционного анализа можно оценить степень взаимосвязи между пределом прочности древесины при статическом изгибе и при сжатии вдоль волокон, выявить наличие статистической связи между уровнем специализации лесопильных предприятий по сечениям пиломатериалов и себестоимостью их производства и т. д.

Будем говорить, что между двумя случайными величинами имеется статистическая связь, если при изменении одной из них меняется распределение другой. Для оценки статистической связи по данным эксперимента широко используется выборочный коэффициент корреляции. Пусть проведено наблюдений и в каждом из них определялись значения двух параметров (признаков) и . Следовательно, имеются две одновременно получаемые выборки:

По каждой из них найдем среднее арифметическое , а также выборочный стандарт и . Выборочный коэффициент корреляции рассчитывается по формуле

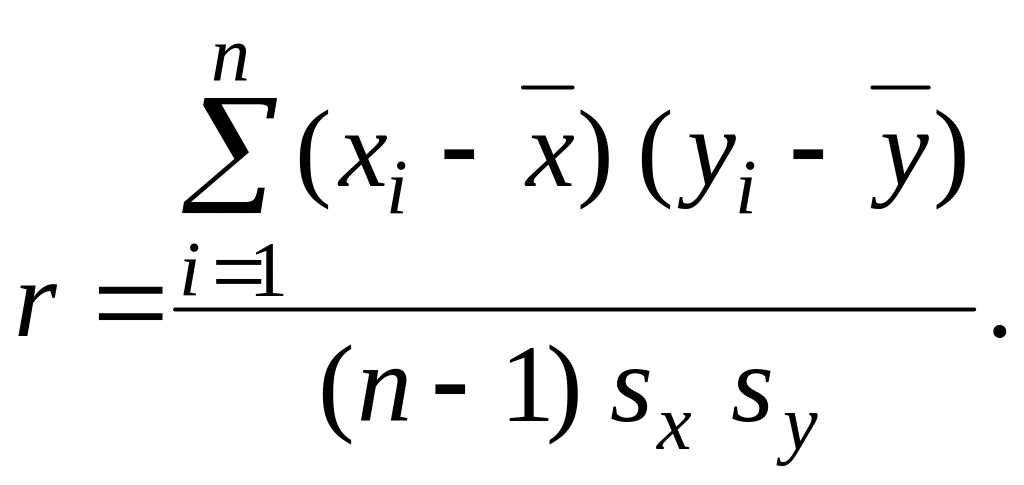(2.23)

или

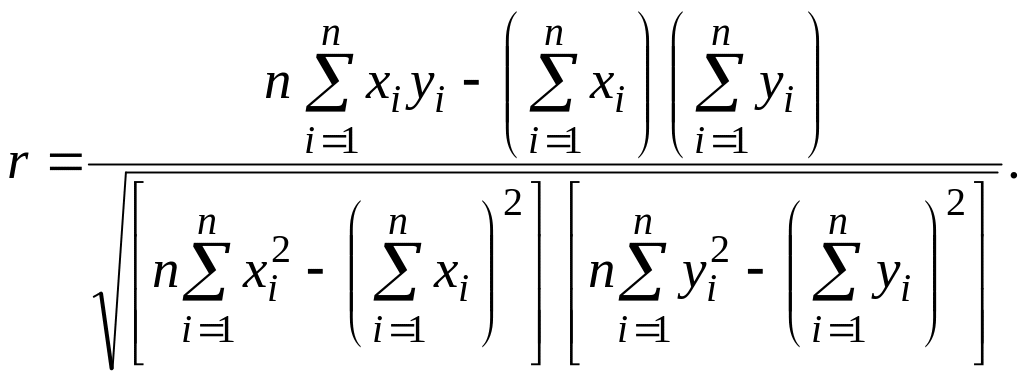(2.24)

При расчетах полезно иметь в виду, что выборочный коэффициент корреляции не изменяется при изменении начала отсчета и масштаба измерения, .

Коэффициент корреляции всегда лежит в пределах . Он характеризует не всякую, а только линейную зависимость между случайными величинами. При положительном можно предполагать, что с возрастанием одной из случайных величин, другая в среднем тоже возрастает. При отрицательном с ростом одной из них другая величина будет в среднем убывать. Чем ближе величина к (+ 1) или к (–1), тем больше степень линейной зависимости между рассматриваемыми случайными величинами. Значение , равное нулю, свидетельствует об отсутствии линейной статистической связи между ними. Такие случайные величины называются некоррелированными. Обычно величина оказывается не равной нулю. Для выяснения того, будут ли некоррелированными в этом случае признаки , вычисляют величину

(2.25)

Ее сравнивают с табличным значением критерия Стьюдента, найденным при выбранном уровне значимости и числе степеней свободы . Если , принимается гипотеза о некоррелированности величин . В противном случае коэффициент корреляции значимо отличается от нуля, т. е. между величинами существует линейная статистическая связь.

Если требуется исследовать статистическую связь между тремя случайными величинами, то пользуются коэффициентом множественной корреляции. Так, для оценки степени статистической связи случайной величины с величинами рассчитывают выборочный совокупный коэффициент корреляции по формуле

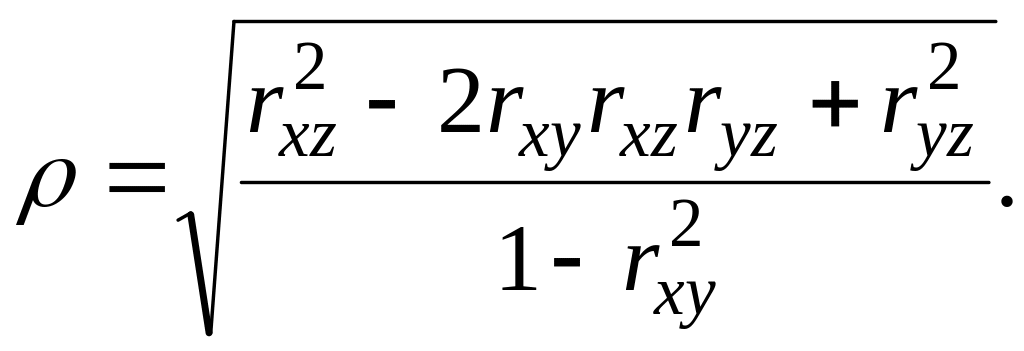(2.26)

где коэффициенты корреляции соответственно между величинами , , .

Величина лежит в пределах и, так же как и обычный коэффициент корреляции, служит для оценки линейной статистической связи.