14

Лекция 2 статистическая физика

9.Функции распределения

9.1. Микросостояние. Вероятность. Средние значения

9.2. Распределение Максвелла.

9.3. Распределение молекул по модулям скорости

9.4. Формула Максвелла в приведенном виде

9.5. Распределение по энергиям молекул

Статистическая физика— это раздел физики, в котором

1. изучают свойства макросистем, исходя из

• индивидуальных свойств составляющих макросистему частиц

• и взаимодействий между ними.

2. оперирует со средними значениями параметров очень большого числа частиц Т.к. описание движения каждой частицы макросистемы (а их порядка 10²² - 10²³) — задача совершенно немыслимая.

3. Колоссальное число частиц в макросистеме приводит, несмотря на очевидный хаос, к появлению новых, статистических закономерностей. Их изучение и делает возможным описание макросистем на основе сведений о свойствах отдельных частиц.

4. Основу статистической физики составляет теория вероятностей

9.1. Микросостояние. Вероятность. Средние значения

О вероятности.. Исходные понятия этой теории — событие и вероятность.

Событие — это, например,

- выпадение одного из шести номеров при бросании игрального кубика.

- Или при измерении скорости молекул газа: разбив возможные значения скоростей на отдельные интервалы (i = 1, 2,...) и обнаружив, что скорость молекулы попала в i-й интервал, мы говорим об i-м событии.

В дальнейшем нас будут интересовать лишь такие события, которые являются:

1) случайными, т. е. событиями, условия наступления которых по тем или иным причинам неизвестны и которые поэтому нельзя заранее с уверенностью предсказать;

2) равновозможными или равновероятными — для которых нет никаких оснований ожидать, что при испытаниях они будут вести себя по-разному (например, при бросании игрального кубика или монеты, но никак не бутерброда с маслом).

Вероятность данного случайного события характеризуется кратностью его повторения. Если в N случаях i-e событие происходит N_t раз, то

вероятностью Pi этого события называют величину

Так как на практике N всегда конечно, то для вычисления вероятности стараются, чтобы N и N_i были достаточно большими. Тогда можно считать, что

Ясно, что сумма вероятностей всех возможных результатов измерений равна единице:

Вычисление вероятностей сложных событий.

Рассмотрим две основные теоремы: о сложении и умножении вероятностей на примере игрального кубика.

1. Теорема сложения вероятностей.

Если в результате N бросаний кубика в N_i случаях выпадет число i, а в N_k случаях — k, то вероятность выпадения i или k равна

Это значит, что при бросании кубика вероятность выпадения, скажем, 2 или 5 равна Р = ¹/₆ + ¹/₆ = ¹/₃.

В общем случае эта теорема утверждает: вероятности несовместимых событий складываются. Пример. При бросании игрального кубика вероятность:

а) выпадения четной цифры равна ¹/₆ + ¹/₆ + ¹/₆ = ¹/₂

б) того, что не выпадет 2, равна ⁵/₆

2. Теорема умножения вероятностей.

Найдем вероятность того, что при двух бросаниях кубика выпадет последовательно i и k. Рассмотрим N двойных бросаний.

Пусть первый из каждой пары бросков дал i в N_t случаях (так что .

Теперь выделим из этих N_i случаев те N_k событий, когда второй бросок кубика давал k (так что ).

Тогда искомая вероятность

Значит, вероятность того, что при двух бросаниях кубика выпадут, допустим, сначала 2, а затем 5, равна ¹/₆ • ¹/₆ = ¹/₃₆-

В общем случае теорема умножения вероятностей утвержда­ет: вероятность совмещения двух или нескольких событий равна произведению вероятностей каждого их них в отдельно­сти.

Пример. Вероятность того, что при двух бросаниях кубика:

а) выпадут две 5, равна ¹/₆ • ¹/₆ = ¹/₃₆

б) не выпадет ни одной 5, равна ⁵/₆ • ⁵/₆ = ²⁵/₃₆;

в) выпадет одна 5, равна (¹/₆ • ⁵/₆) + (¹/₆ • ⁵/₆) = ¹⁰/₃₆

Заметим, что Р_а + Р₆ + Р_в = 1, как и должно быть.

Для исследования и количественного описания статистических закономерностей вводят, в статистической физике, многомерное пространство, которое называется фазовым пространством.

Это такое пространство, в котором в качестве координатных осей выбираются координаты X_i и импульсы p_i частиц, входящих в макроскопическую систему А.

• Если в систему входит N частиц, то размерность фазового пространства 3N+3N=6N

(3N координатных осей - проекции координат всех частиц системы А,

3N координатных осей - проекции импульсов).

• Р

  P

  dP

  a

  dx

  х Рис.1.

  Рис.1 x

  ис.1. Если система характеризуется одной степенью свободы, то фазовое пространство двухмерно

- Точка а фазового пространства характеризует микросостояние системы А (т.е. совокупность всех координат X_i и импульсов p_i всех частиц системы А) в некоторый момент времени и называется фазовой точкой.

- кривая на рис.1 .Из-за взаимодействия частиц между собой и с окружающим пространством положение фазовой точки а в следующий момент времени изменится, т.е. фазовая точка сместится по фазовой траектории

Если через каждые измерять X_i и p_i частиц системы А и наносить точку в фазовом пространстве, то спустя большие время Т в фазовом пространстве получается облако точек.

Эти точки изображают возможные микросостояния системы А, совместимые с данным макросостоянием. За время Т система А побывает во всех возможных микросостояниях, которые совместимы с данным макросостоянием.

Функция распределения.

1. Рассмотрим некоторый объем фазового пространства dV:

dV соответствует значениям координат и импульсов частиц, лежащих в интервале

Если dt - время, в течение которого микросостояние системы А изображается фазовыми точками, находящимися в объеме dV,

то величину можно рассматривать, как частоту события (точнее - как вероятность) того, что при наблюдении за системой А , эта система в произвольный момент времени находится в одном из микросостояний с координатами x; х+dx и импульсом p; p+dp.

Ясно, что чем больше выбран объем dV, тем больше вероятность застать в нем фазовую точку, т.е. ,

где - функция статистического распределения.

2. Рассмотрим случай, когда случайная величина х имеет непрерывный характер (например, скорости молекул).

Для этого

• разобьем всю область изменения х на отдельные интервалы

• и будем считать число попаданий случайной величины в тот или иной интервал.

Интервалы должны быть

1. во избежание заметных флуктуаций достаточно большими,

• чтобы в каждом интервале число попаданий было 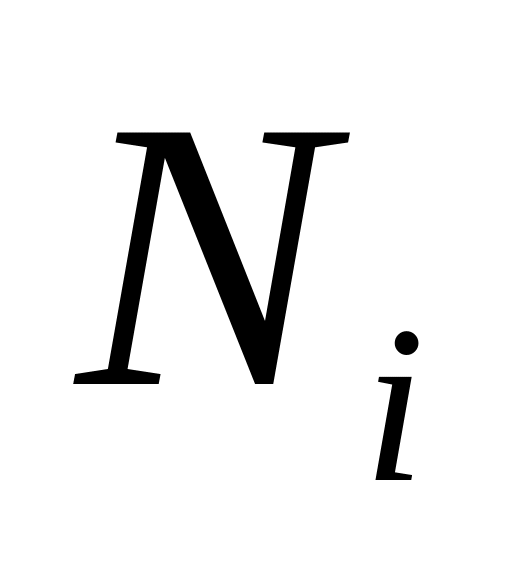>>1

• и чтобы можно было определить вероятность попадания случайной величины в данный интервал.

2. Вместе с тем, интервалы должны быть достаточно небольшими, чтобы более детально характеризовать распределение величины х.

Итак, мы имеем достаточно большое число достаточно небольших интервалов и,

допустим, нам известна вероятность попадания в тот или иной интервал ∆x.

Сама величина ∆ весьма мала, поэтому в качестве характеристики случайной величины берут отношение ∆ /∆x, которое для достаточно малых ∆х не зависит от величины самого интервала ∆x. Это отношение при ∆х —> 0 называют функцией распределения f(х) случайной величины х: .

В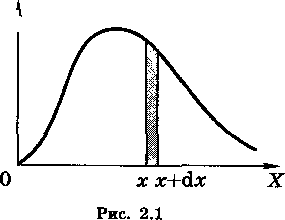 идно, что функции распределения f(х) можно приписать смысл плотности вероятности, т.е. вероятности интересующей нас величины оказаться в единичном интервале вблизи значения х.

В разных случаях функция распределения имеет совершенно различный вид, один из которых в качестве примера приведен на рис. 2.

В соответствии с (1) площадь полоски шириной dx на этом рисунке равна вероятности того, что случайная величина х окажется в пределах интервала (x, x + dx):

.

Вероятность того, что величина х попадает в интервал (a,b):

Ясно, что вероятность того, что величина х может принять хотя бы какое-нибудь значение (достоверное событие), равна единице. Это называют условием нормировки:

,

где интегрирование производится по всему интервалу возможных значений величины х.

Из этого условия следует, что вся площадь под кривой f(x) равна единице (см. рис. 1).

Среднее значение величины x можно найти, зная ее нормированную на единицу функцию распределения f(x):

,

интегрирование проводится по интересующему нас интервалу значений х.

Аналогичные формулы справедливы для любой функции φ(x), например,

.

Флуктуации. Вероятность случайного события и экспериментально наблюдаемая доля результатов, когда событие осуществляется, — это не одно и то же. Последняя (доля результатов) испытывает случайные отклонения от предсказываемой вероятности. Именно такого рода отклонения происходят в любых макросистемах. Эти отклонения и обусловливают флуктуации.

Согласно теории вероятности, с увеличением числа N испытаний относительная флуктуация любой величины уменьшается по закону 1/4N. Именно грандиозность числа N молекул и объясняет, почему макроскопические законы, получаемые на основе статистических представлений о движении частиц макросистемы, оказываются точными.

Понятие бесконечно малого объема dV макросистемы - такой объем, размеры которого ничтожны по сравнению с размерами самой макросистемы, но все же намного превосходящие характерный размер ее микростроения.

Каждая бесконечно малая область, предполагается, содержит число частиц dN настолько большое, что относительной флуктуацией их можно пренебречь.

Д емонстрация статистического распределения. Великолепная демонстрация статистического характера распределения может быть показана на так называемой доске Гальтона. Она представляет собой

• вертикальную панель, в которую равномерно и достаточно густо вмонтированы горизонтальные стержни — точки на рис. .

• Внизу под решеткой из стержней расположены узкие одинаковые вертикальные ячейки.

• Вверху над стержнями помещена воронка, в которую можно сыпать, например, зерна пшена.

• И все это (воронка, стержни и ячейки) прикрыто с передней стороны стеклом.

Если бросить в воронку одно зернышко, то при падении оно испытает много столкновений со стержнями, после чего попадет в одну из ячеек. В какую именно — предсказать совершенно невозможно из-за множества случайных факторов, влияющих на его движение. Можно говорить лишь о вероятности попадания зернышка в ту или иную ячейку. Естественно ожидать, что попадание в центральные ячейки более вероятно, чем в крайние. Опыт это подтверждает: если сыпать пшено в воронку непрерывно, то в центральные ячейки действительно попадает больше всего зернышек.

При очень большом числе зернышек возникает вполне определенная статистическая закономерность распределения их по ячейкам, как показано на рис.

Повторив опыт, обнаружим то же распределение, ту же закономерность (это распределение называют нормальным законом Гаусса).

Таким образом, мы имеем наглядную, убедительную демонстрацию того, как проявляют себя статистические законы через большое число случайных событий