
- •Лекция 2 статистическая физика
- •9.Функции распределения
- •Основу статистической физики составляет теория вероятностей
- •9.1. Микросостояние. Вероятность. Средние значения
- •9.2. Распределение Максвелла
- •9.3. Распределение молекул по модулям скорости
- •Наиболее вероятной скорости
- •9.4. Формула Максвелла в приведенном виде
- •5.3.5. Распределение по энергиям молекул
- •9.6. Опытная проверка распределения Максвелла
- •9.7. Распределение Больцмана
- •9.8. Барометрическая формула
- •9.9. Распределение Больцмана при дискретных уровнях
- •10.10. Закон распределения Максвелла—Больцмана
9.2. Распределение Максвелла
Закон распределения по скоростям молекул газа, находящегося в термодинамическом равновесии, был найден Максвеллом (1859).
Рассмотрим физический смысл закона Максвелла и некоторых его следствий.
Представим себе
- пространство
скоростей с прямоугольными координатными
осями, по которым будем откладывать
значения проекций
![]() отдельных молекул.
отдельных молекул.
-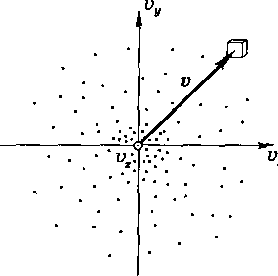 Тогда скорости каждой молекулы
будет соответствовать точка в этом
пространстве — конец вектора
Тогда скорости каждой молекулы
будет соответствовать точка в этом
пространстве — конец вектора
![]() .
.
- Из-за столкновений молекул положения точек будут стремительно меняться, но их распределение в целом будет оставаться неизменным, поскольку макросистема находится в термодинамическом равновесии.
В
Рис.3.![]() (но не от
).
(но не от
).
Пусть макросистема (газ) содержит N молекул.
Выделим в некоторой точке — конце вектора — малый объем
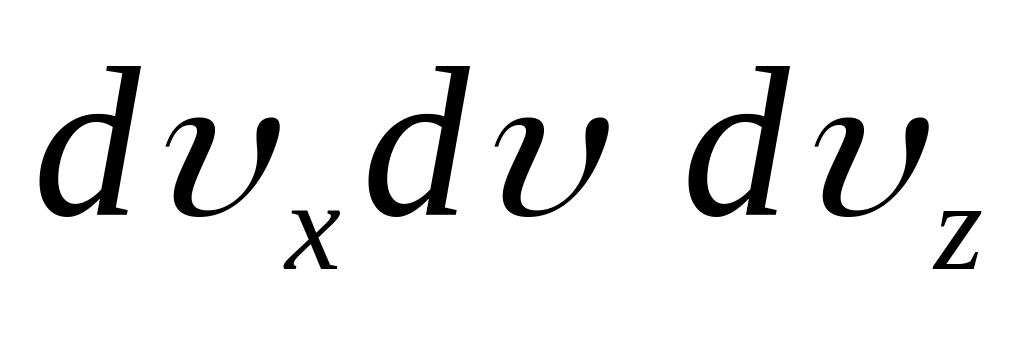
(рис. 3, где ось
![]() направлена на нас).
направлена на нас).
Относительное число точек (молекул) в этом объеме, или другими словами,
1. вероятность dP того, что скорость молекулы, т.е. конец вектора , попадет в этот объем, можно записать так:
![]() ,
(2)
,
(2)
где
![]() имеет
смысл объемной
плотности вероятности.
имеет
смысл объемной
плотности вероятности.
Вероятность же того, что молекула (точка) будет иметь проекции скорости в интервале (
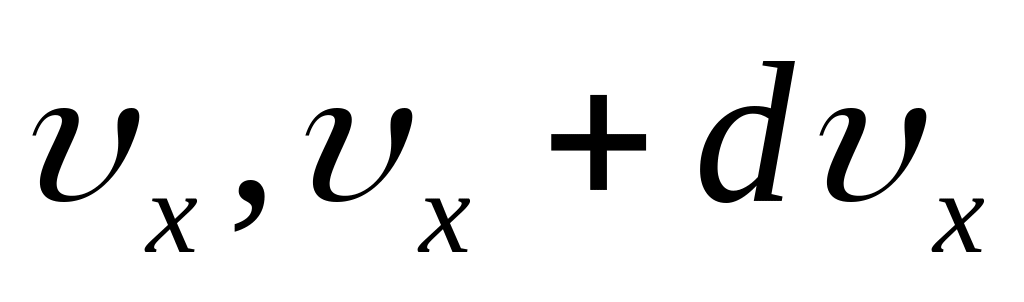 ),
),
есть
![]() , (3)
, (3)
где
![]() —
функция распределения по
—
функция распределения по
![]() .
.
Выражение (3) — это по существу
интеграл (2) по
![]() и
,
т.е. относительное число молекул
(точек) в тонком плоском слое от
до
+ d
.
и
,
т.е. относительное число молекул
(точек) в тонком плоском слое от
до
+ d
.
3. Вероятности того, что молекула
имеет проекции скорости в интервалах
(
,
+d
),
(![]() и
(
и
(![]() )
являются независимыми, поэтому в
соответствии с теоремой об умножения
вероятностей независимых событий можно
записать
)
являются независимыми, поэтому в
соответствии с теоремой об умножения
вероятностей независимых событий можно
записать
![]() (4)
(4)
Из соображения равноправия осей , и ясно, что функции φ должны одинаковым образом зависеть от соответствующих проекций скоростей. Сопоставив (4) с (2), находим
![]() .
(5)
.
(5)
После преобразований (с учетом условия нормировки) получаем
![]() ,
,
аналогичный вид имеют функции
![]() и
и
![]() .
.
И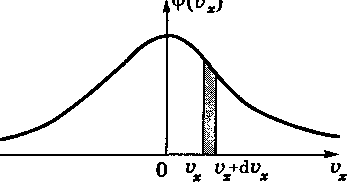 тогда согласно (5)
тогда согласно (5)
![]() .
(6)
.
(6)
рис. 4. График
функции
![]()
Он совпадает с гауссовой кривой погрешностей. Площадь тонированной полоски на рис. 4 — это вероятность того, что проекция скорости молекулы лежит в интервале ( , +d ).
Функция (6) нормирована на единицу,
т.е. площадь под кривой
![]()
Интегрирование в пределах от -∞ до +∞ не означает, что в газе есть молекулы с такими большими скоростями. Это следует рассматривать только как вычислительный прием. Молекул с весьма большими скоростями очень мало, и они практически не вносят никакого вклада в нормировочный интеграл. Это и позволяет записывать такие пределы.
9.3. Распределение молекул по модулям скорости
Найдем вероятность или относительное
число молекул, модуль скорости которых
заключен в интервале (![]() ).
).
р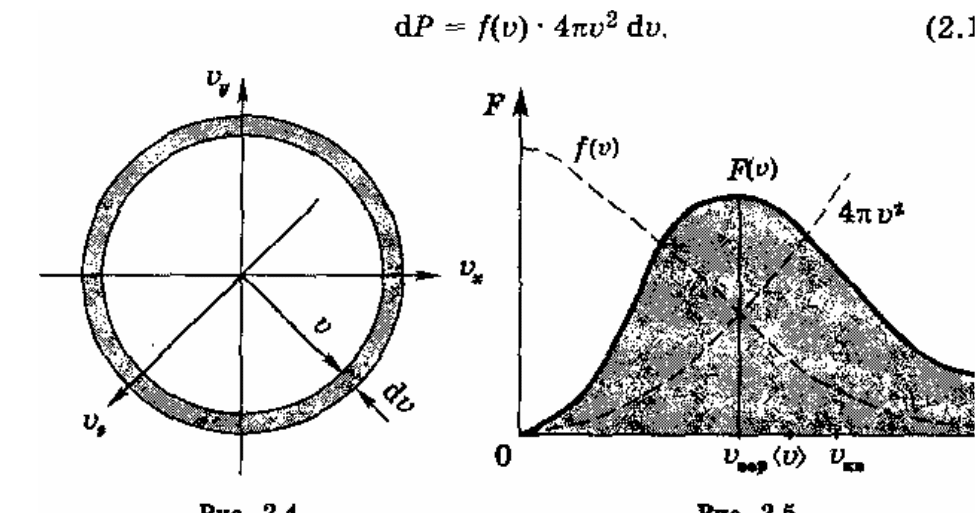 ис.
5. Таким молекулам
ис.
5. Таким молекулам
соответствуют все точки, попадающие в шаровой слой с радиусами и
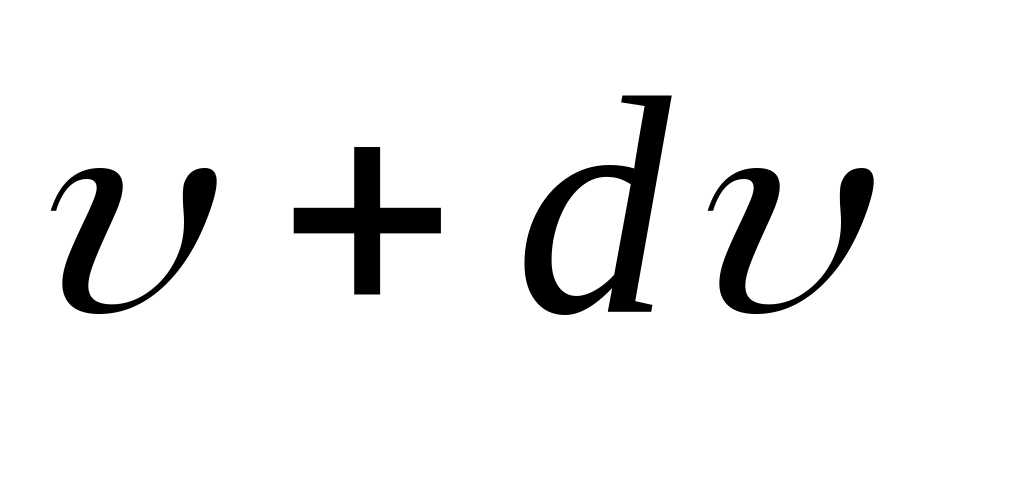 .
.Объем этого слоя равен произведению поверхности слоя на его толщину, т.е.
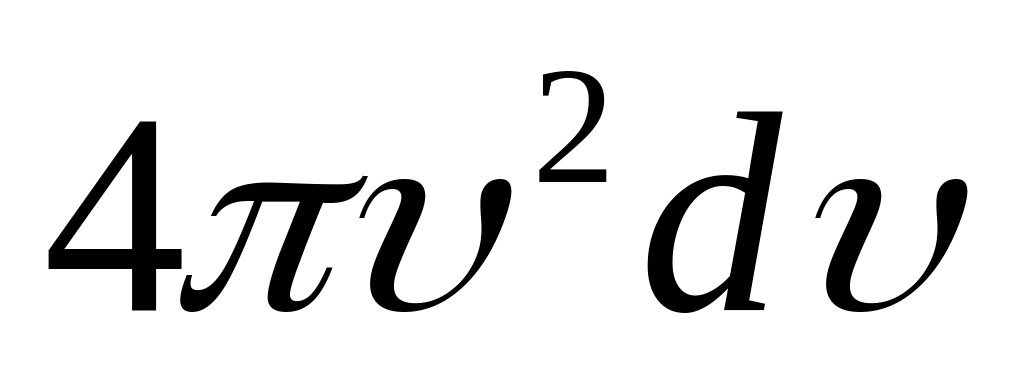
объемная же плотность вероятности
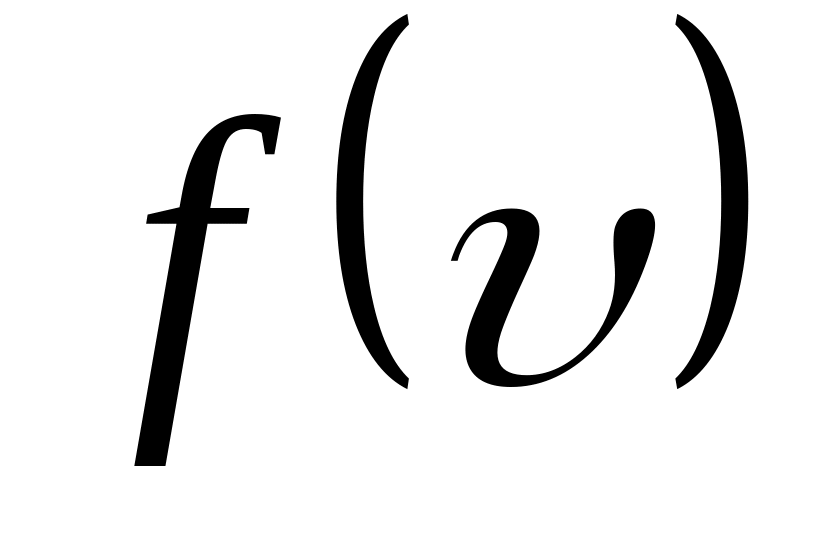 во всех точках слоя одинакова.
Рис 5 рис.
6
во всех точках слоя одинакова.
Рис 5 рис.
6вероятность попадания в этот слой согласно теореме сложения вероятностей,
![]()
Величина
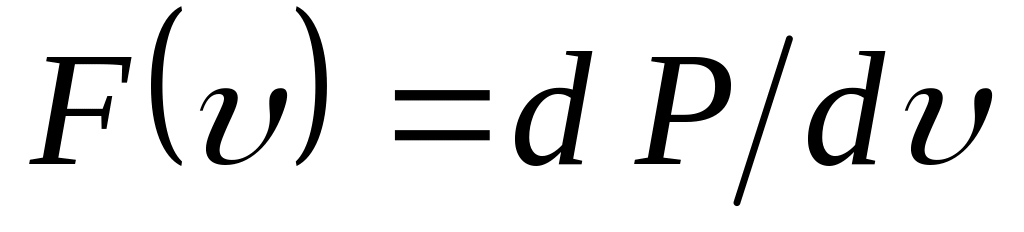 характеризует искомую вероятность,
т.е
характеризует искомую вероятность,
т.е
![]() .
.
Учитывая (6), получим:![]() .
(7)
.
(7)
Эта формула представляет собой закон распределения Максвелла по модулю скорости.
Вид
функции
![]() показан на рис. 6.
показан на рис. 6.
Эта
функция тоже нормирована на единицу;
![]() .
.
На рис.6 пунктиром представлена “конструкция” (сомножители) функции , один из сомножителей которой .
Заметим, что в отличие от площадь под кривой физического смысла не имеет.
Полученные Максвеллом распределения по скоростям не зависят
ни от структуры молекул,
ни от того, как они взаимодействуют друг с другом.
Поэтому они применимы не только к газам, но и к другим агрегатным состояниям вещества.
Рассмотрим характерные скорости. К ним относятся три скорости:
наиболее вероятная
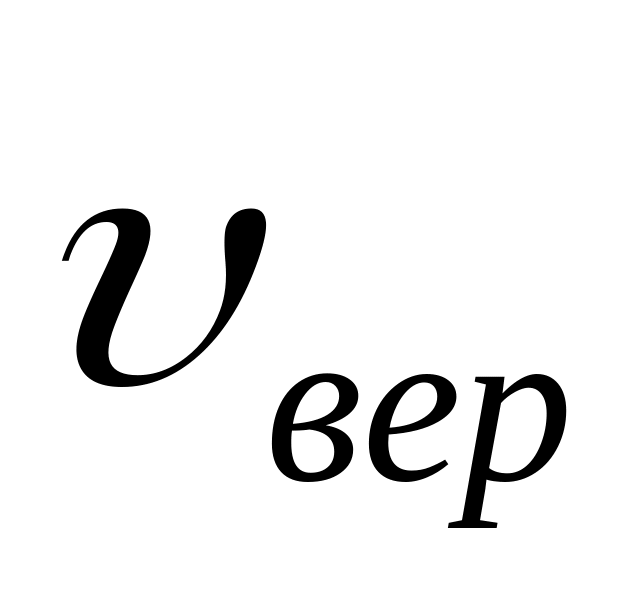 ,
,
средняя
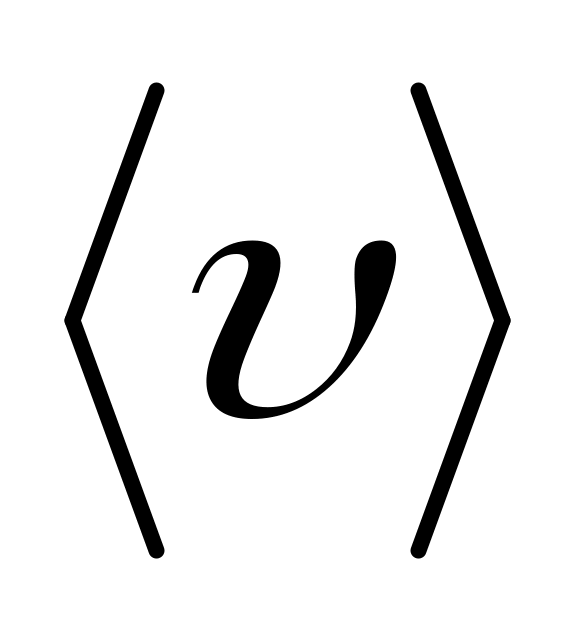 ,
,среднеквадратичная
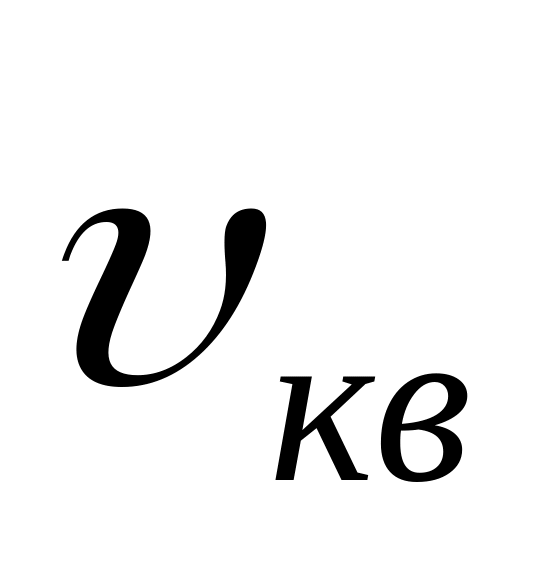 .
.
