Глава 2. Электрические фильтры

2.1. Общие понятия и классификация

Электрическим фильтром называется четырехполюсник, предназначенный для пропускания сигналов одних частот и подавления (задержки) сигналов других частот.

Для оценки частотных свойств фильтра используется понятие полосы пропускания. Полосой пропускания фильтра называется интервал частот, на котором величина собственного затухания фильтра не превышает заданного уровня.

Фильтры классифицируются по следующим признакам:

1.По пропускаемым частотам:

- фильтры низких частот (низкочастотные) пропускают сигналы, начиная с нулевой частоты и до некоторой граничной частоты;

- фильтры высокой частоты (высокочастотные) пропускают сигналы, начиная с некоторой граничной частоты до сколь угодно большого их значения;

- фильтры полосовые пропускают сигналы, лежащие в определенной полосе частот, ограниченной нижним и верхним значениями;

- режекторные фильтры не пропускают сигналы только в определенной полосе частот и по частотным свойствам являются противоположностью полосовым фильтрам.

2. По схемам простейших звеньев:

- Г-образные;

- Т-образные;

- П-образные.

3. По числу простейших звеньев, используемых в фильтре:

- однозвенные;

- многозвенные (двухзвенные, трехзвенные и т. д.).

4. По виду характеристик:

- фильтры типа – k;

- фильтры типа – m.

5. По типам элементов схемы.

5.1. Пассивные фильтры - без усилительных элементов:

- реактивные (из L-С элементов);

- безиндуктивные (из R-C элементов);

- пьезоэлектрические.

5.2. Активные фильтры:

- фильтры, выполненные с применением транзисторов;

- фильтры, выполненные с применением электронных ламп.

В этой главе основное внимание будет уделено изучению реактивных фильтров, то есть фильтров, которые состоят только из конденсаторов и катушек индуктивности, соединённых определённым образом. В конце главы в разделе 2.5 будут рассмотрены безиндуктивные фильтры.

2.2. Основные схемы фильтров. Характеристические параметры и условия пропускания фильтров

2.2.1Основные схемы фильтров. Характеристические параметры фильтров

Электрический фильтр представляет собой четырёхполюсник, поэтому при анализе фильтров широко используется теория четырёхполюсников. Основные схемы фильтров совпадают со схемами замещения четырёхполюсников, рассмотренных выше (Глава 1, раздел 1.9). Элементами фильтров могут быть как единичные элементы – резистор, конденсатор, катушка индуктивности, так и некоторые схемные решения из этих элементов – последовательные или параллельные контура. Элементы, из которых состоят фильтры, принято обозначать через Z₁ и Z₂. Из сказанного следует, что элементы фильтров являются комплексными величинами, однако точки над этими обозначениями принято не ставить.

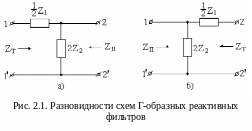Простейшая схема фильтра состоит из двух элементов, соединённых по Г - образной схеме (рис. 2.1). При этом, как видно из рисунка, возможны два варианта соединения элементов. Это приводит к изменению входных и выходных сопротивлений данного типа фильтров. Такие фильтры являются однозвенными.

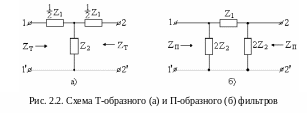
Более сложным схемным решением фильтров являются Т – образные и П – образные фильтры (рис. 2.22). Эти фильтры могут быть получены путём каскадного соединения Г – образных фильтров, меняя последовательность их соединения. Подробно этот вопрос рассмотрен выше, в разделе 1.9 (рис. 1.21).

При анализе свойств фильтров интерес представляют его характеристические параметры – характеристические сопротивления и мера затухания. Характеристические сопротивления фильтров принято обозначать через Z_Т и Z_П. Это связано с понятиями Т – образного и П – образного фильтров.

Определим характеристические сопротивления для Г – образного фильтра схема рис. 2.1,а. Так как характеристические сопротивления определяются по формулам (1.9), то необходимо найти параметры холостого хода и короткого замыкания для схемы рис. 2.1,а :

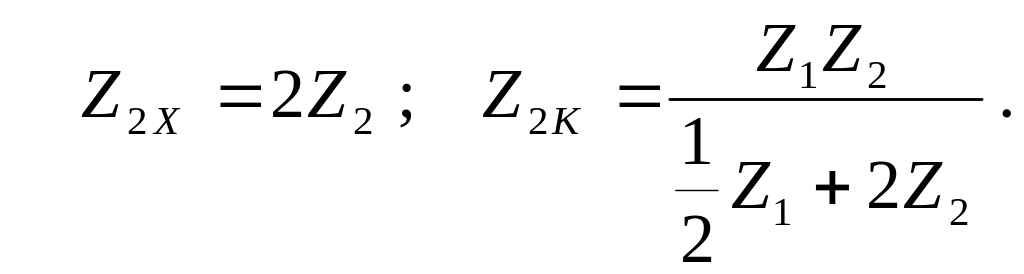(2.1)

Для фильтра рис. 2.1,а входное характеристическое сопротивление обозначим через Z_Т, а выходное через Z_П. По формуле (1.9) находим эти характеристические сопротивления:

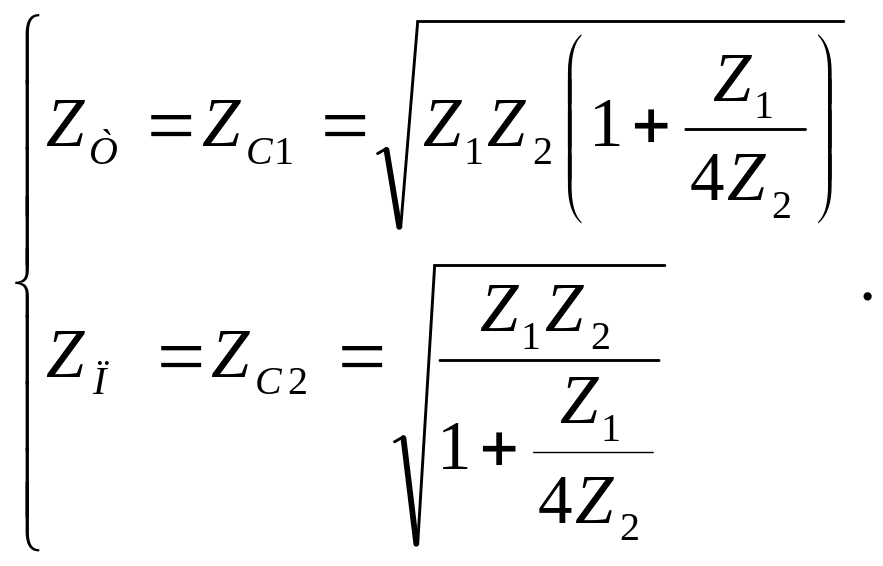(2.2)

Найдём характеристические сопротивления для второго Г – образного фильтра (рис. 2.1,б). Для этого определим параметры холостого хода и короткого замыкания для этой схемы:

.

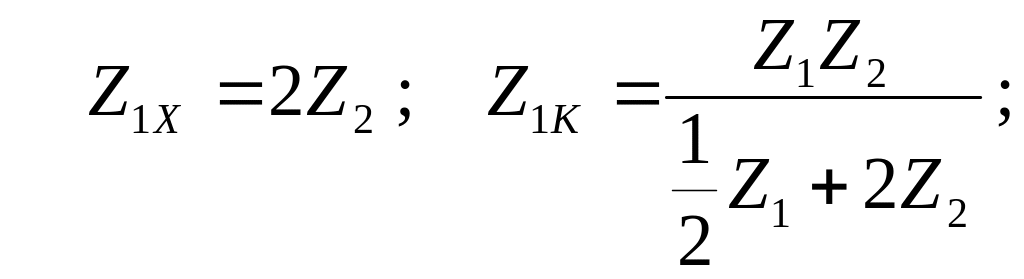
Подставляем полученные параметры холостого хода и короткого замыкания в формулу (1.9) и находим характеристические сопротивления для этой схемы Г – образного фильтра:

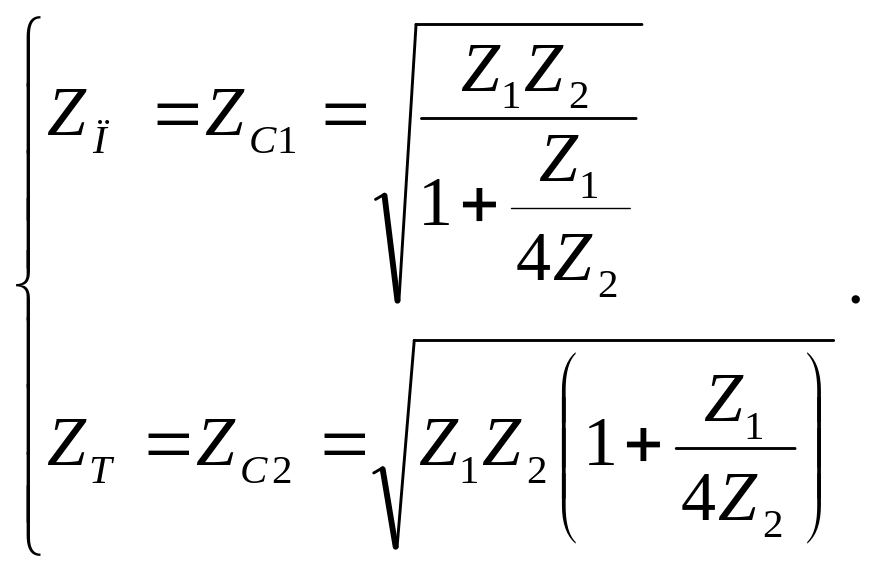
Сравнивая эти сопротивления с сопротивлениями фильтра на рисунке 2.1,а (2.2), видим, что их сопротивления Z_Т равны и их сопротивления Z_П также равны.

Определим затухание для Г – образного фильтра. Величина затухания Г – образного фильтра, как будет показано, в два раза меньше затухания Т – образного и П – образного фильтров, с чем не трудно согласиться исходя из их схемного решения. Поэтому затухание Г – образного фильтра обозначают через g/2. Определяя затухание Г – образного фильтра с помощью формул (1.12) для каждой из схем, обнаруживается, что для каждой схемы затухание определятся одинаково по следующим формулам:

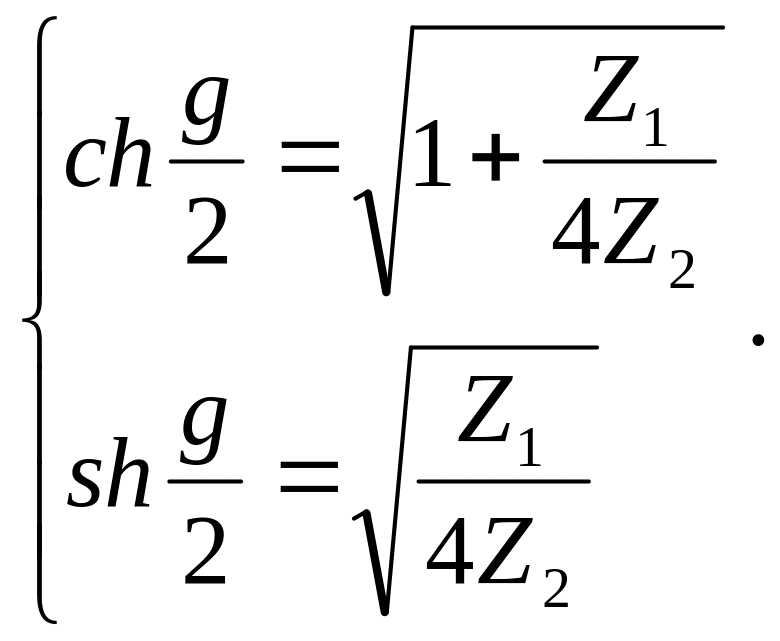(2.3)

Справедливость последнего утверждения предлагается проверить.

Определим характеристические параметры для Т - образной схемы фильтра (рис. 2.2,а). Вначале находим параметры холостого хода и короткого замыкания. Так как, с точки зрения теории четырехполюсников, схема Т - образного фильтра являются симметричной, что видно из схемы, то очевидно выполнение следующих равенств:

С учетом этого находим параметры холостого хода и короткого замыкания для Т – образного фильтра:

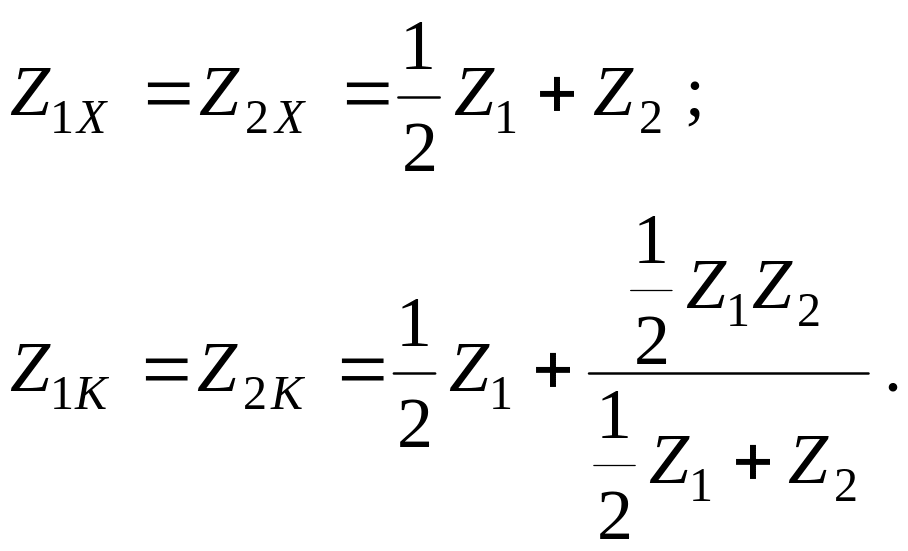(2.4)

Подставляя (2.4) в (1.9), находим характеристические сопротивления Т – образного фильтра:

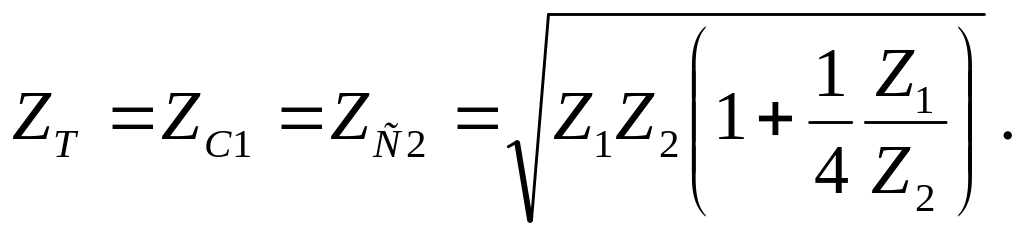(2.5)

Сравнивая (2.5) с (2.2), видим, что Z_T для Т-образной схемы фильтра полностью совпадает с Z_T для Г-образной схемы фильтра.

Определим характеристические сопротивления для П – образного фильтра (рис. 2.2,б). Вначале находим параметры холостого хода и короткого замыкания. Так как, с точки зрения теории четырехполюсников, схема П - образного фильтра являются симметричной, то очевидно выполнение следующих равенств:

С учетом этого находим параметры холостого хода и короткого замыкания для П – образного фильтра:

; .

Найденные параметры холостого хода и короткого замыкания подставляем в формулы (1.9) и находим характеристические сопротивления для П – образного фильтра:

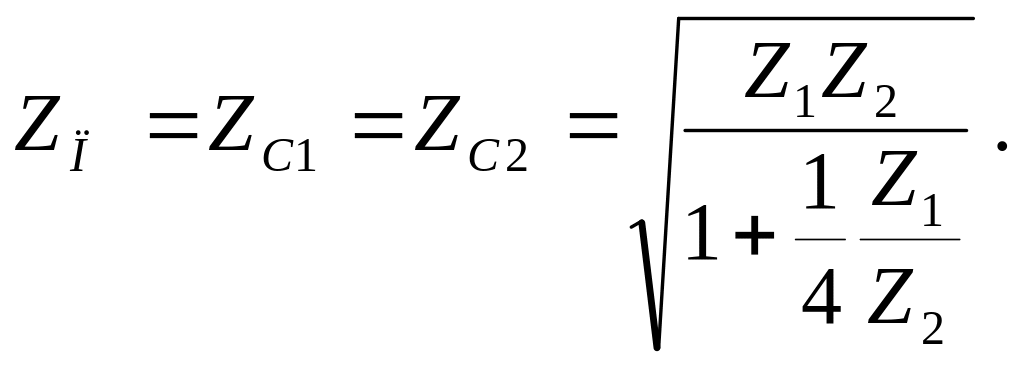(2.6)

Сравнивая (2.6) и (2.2), видим, что Z_П для П - образной схемы совпадает с Z_П для Г - образной схемы.

Определим затухание Т - образного фильтра. Подставляя найденные выше параметры холостого хода и короткого замыкания для этого фильтра в (1.12) находим:

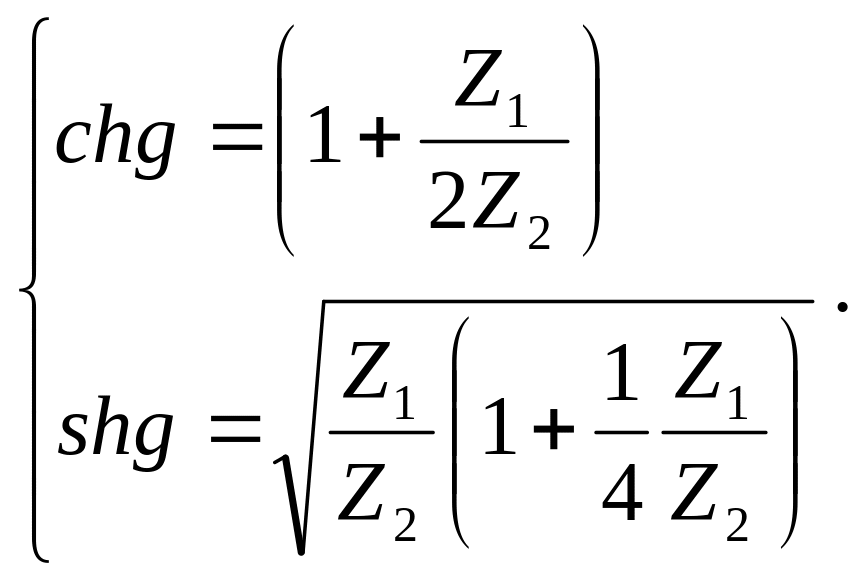(2.7)

Поступая аналогично для П - образной схемы фильтров, находим, что его затухание определяется также выражениями (2.7). Предлагается это утверждение проверить самостоятельно.

Справедливость утверждения, что затухание Г-образного фильтра равно половине затухания Т - образного и П - образного фильтров, можно доказать с помощью гиперболической функции половинного аргумента:

(2.8)

Подставляя в (2.8) соответствующие выражения из (2.3) и (2.7), получаем тождество. Предлагается проверить это самостоятельно.

Подводя итоги проведённого анализа можно сказать, что характеристические сопротивления имеющие одинаковые индексы (Z_Т или Z_П ) у всех рассмотренных фильтров определяются по одним и тем же формулам. Меры затухания Т – образного и П – образного фильтров определяются с помощью одних и тех же формул, а мера затухания у Г- образного фильтра в два раза меньше меры затухания Т – образного и П – образного фильтров. Это легко понять, если вспомнить, что они получены путём каскадного соединения Г – образных фильтров. Тогда процесс подавления сигнала в Т – образном и П – образном фильтрах можно представить как покаскадное подавление сигнала. Вначале происходит подавление сигнала первым каскадом Г – образного фильтра (рис. 1.21), а затем этот, уменьшенный сигнал, проходит через второй каскад, который обладает такими же подавляющими свойствами. Здесь происходит последующее подавление сигнала на такой же уровень, так как меры подавления каждого каскада равны.

2.2.2 Условия пропускания фильтров

Как было сказано выше, электрические фильтры обладают свойством пропускать сигналы в некотором диапазоне частот и не пропускать (ослаблять, подавлять) их на других частотах. Интервал пропускаемых частот, как отмечалось, характеризуется полосой пропускания. Расположение полосы пропускания на всём интервале частот (низкие частоты, высокие частоты и так далее) определяется схемным решения фильтра, то есть типами элементов и видом их соединения. Величина интервала полосы пропускания определяется величинами параметров элементов. Очевидно, что свойства фильтров пропускать или подавлять сигнал оценивается с помощью меры затухания (1.10):

,

где a – величина собственного затухания четырехполюсника, отображающая изменение сигнала по модулю;

b – коэффициент фазы затухания четырёхполюсника, отображающий изменение фазы сигнала.

При определении условий пропускания фильтром сигналов принято считать, что в интервале пропускаемых частот величина собственного затухания фильтра равна нулю:

(2.9)

Тогда мера затухания фильтра в интервале пропускаемых частот будет мнимой величиной:

(2.10)

Из всех найденных гиперболических функций от меры затухания (2.7) при мнимом значении аргумента только гиперболический косинус от мнимого аргумента имеет вещественное значение. Это наиболее удобно в решении поставленной задачи. Из свойств гиперболических функций комплексного аргумента известно:

Тогда с учётом первого выражения (2.7) получаем:

(2.11)

Как известно:

. (2.12)

Тогда из (2.12) и (2.11) получаем неравенство:

(2.13)

Неравенство (2.13) позволяет рассмотреть следующих два неравенства. Первое имеет вид:

Отсюда находим:

Граничное условие этого неравенства имеет вид:

(2.14)

Это выражение является одним из условий пропускания фильтра, из которого, как увидим, легко определяется одна из граничных частот полосы пропускания.

Второе неравенство из (2.13) имеет вид:

Отсюда находим:

Второе граничное условие имеет вид:

(2.15)

С помощью (2.15) определяется вторая граничная частота полосы пропускания. Граничные условия (2.14) и (2.15) получены для симметричных схем фильтров, которые нагружены на согласованную нагрузку. При построении реактивных фильтров в качестве сопротивлений Z₁ и Z₂ должны использоваться сопротивления с разными знаками:

(2.16)

Следует подчеркнуть, что здесь X₁ и X₂ являются положительными величинами. Из (2.16) следует, что если одно из сопротивлений индуктивность, то другое сопротивление должно быть конденсатором и на оборот. Справедливость этого требования можно проверить на выполнении одного из граничных условий пропускания фильтра. Из (2.14) можно записать:

.

Подставим в это выражение (2.16):

.

Действительно, первое граничное условие (2.14) буде выполняться, если Z₁ и Z₂ будут удовлетворять требованиям (2.16). При использовании сопротивлений Z₁ и Z₂ одного знака (только конденсаторов или только индуктивностей) рассмотренные схемы не обладают фильтрующими свойствами. Они становятся только индуктивными или емкостными делителями напряжения.

При анализе частотных свойств фильтров интерес представляет не только полоса пропускания, но характер изменения собственного затухания фильтра за пределами полосы пропускания. В идеальном фильтре в пределах полосы пропускания подавление должно равняться нулю, а за пределами полосы пропускания собственное затухание фильтра должно равняться бесконечности (сразу же на границе полосы пропускания). В реальных фильтрах это далеко не так. Очень важно знать на сколько круто (резко) возрастает затухание за пределами полосы пропускания, так как незначительное его возрастание приведёт к незначительному подавлению, а значит к частичному пропусканию сигналов, лежащих за границе полосы пропускания.

Для рассмотрения этого вопроса необходимо найти зависимость подавления фильтра от частоты. Воспользуемся любым из полученных соотношений для меры затухания (2.3) или (2.7). Как показала практика, для анализа этого вопроса наиболее удобным является выражение затухания через гиперболический синус из системы (2.3):

(2.17)

Уже отмечалось, что фильтр будет обладать фильтрующими свойствами, если сопротивления имеют противоположные знаки (2.16). Подставляя (2.16) в (2.17), получим:

(2.18)

Выражение (2.18) является чисто мнимым, то есть его вещественная составляющая равна нулю. Гиперболический синус от комплексного аргумента имеет вид:

Тогда, учитывая, что , выражение (2.18) принимает вид:

(2.19)

Левые части (2.18) и (2.19) равны. Напомним, что два комплексных числа равны, если равны их вещественные и мнимые части. Сравнивая вещественные составляющие правых частей (2.18) и (2.19), получаем следующее уравнение:

(2.20)

Сравнивая мнимые составляющие правых частей (2.18) и (2.19), получаем ещё одно уравнение:

(2.21)

Уравнение (2.20) имеет место при двух возможных условиях.

Первое условие:

При этом условии а=0, что соответствует требованию пропускания фильтра. Как известно, гиперболический косинус от нуля равен единице, тогда из (2.21) следует:

Из последнего соотношения можно получить зависимость коэффициента фазы (b) от частоты:

.

Второе условие выполнения равенства (2.20) состоит в следующем:

Косинус будет равен нулю, если . Тогда для соотношения (2.21) должно выполняться:

.

В (2.21) значение синуса может быть только положительным, так как правая часть (2.21), состоящая из положительных величин, как было отмечено выше, является положительной величиной. С учётом рассмотренного, выражение (2.21) принимает вид:

(2.22)

Обозначим:

, , (2.23)

где - собственное затухание Г – образного фильтра.

Учитывая, что собственное затухание является положительной величиной, а , воспользуемся формулой для обратной гиперболической функции от (2.22), с учётом введённых обозначений (2.23):

(2.24)

При анализе собственного затухания Т - образного и П - образного фильтров результаты вычислений по (2.24) необходимо удваивать.

В заключении необходимо отметить два важных момента. Первый состоит в том, что при определении граничных частот используются следующие граничные условия:

;

Здесь сопротивления Z – комплексные величины и при вычислении должны учитываться знаки сопротивлений.

Второй состоит в том, что при вычислении затухания по формуле:

,

где ,

необходимо учитывать следующее:

- эта формула используется только для определения затухания в Г – образных фильтрах, так как соотношение (2.17), из которого получена формула для затухания, взята из системы (2.3) для Г – образных фильтров;

- сопротивления X₁ и X₂ имеют положительные значения, так как знаки этих сопротивлений были учтены в (2.16) и при переходе от (2.17) к (2.18).

2.3. Фильтры типа – k

Фильтры типа – k состоят из соединённых определённым образом взаимообратимых двухполюсников.

Два двухполюсника являются взаимообратимыми, если произведение их сопротивлений не зависит от частоты. Простейшими такими двухполюсниками являются конденсатор и индуктивность. Произведение их сопротивлений равно:

Такие двухполюсники, как последовательный и параллельный резонансные контура, также являются взаимообратимыми. Найдем произведение их сопротивлений:

Результат таких произведений обозначается через k². Фильтры, состоящие из взаимообратимых двухполюсников, называются фильтрами типа – k.

Низкочастотные фильтры.

На рисунке 2.3 представлены варианты схем низкочастотных фильтров типа – k.

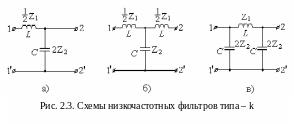По схемным решениям на рисунке 2.3 представлены Г – образный фильтр (рис. 2.3,а), Т- образный фильтр (рис. 2.3,б) и П – образный фильтр (рис. 2.3,в). Обратим внимание на то, что в этих фильтрах используются элементы, имеющие разные знаки сопротивлений и удовлетворяющие требованию (2.16).

Рассмотрим частотные свойства этих фильтров. Для этого необходимо найти граничные частоты, определяющие полосу пропускания. Расположение полосы пропускания на оси частот покажет действительно ли эти фильтры являются низкочастотными.

Как отмечалось, граничные условия пропускания (2.14) и (2.15) позволяют определить граничные частоты, определяющие границы полосы пропускания фильтра. Определить граничные частоты можно аналитически и графически. Вначале найдём аналитически граничные частоты для схемы, например, рисунок 2.3,б. Находим для этой схемы Z₁ и Z₂:

.

Из условия (2.15) находим первое значение граничной частоты:

;

Из условия (2.14) находим второе значение граничной частоты:

Итак, полоса пропускания этого фильтра лежит в интервале от нулевой частоты ω₁ до некоторой найденной частоты ω₂. Следовательно, этот фильтр пропускает низкие частоты. Граничные частоты полосы пропускания часто называют частотами среза и обозначаются как ω_с.

Э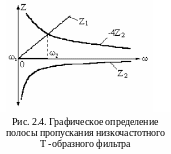 ту же задачу можно решить графически. Для этого необходимо построить графики зависимости сопротивлений Z₁ и Z₂ от частоты. На рис.2.4 построены графики сопротивлений Z₁ и Z₂ и для сопротивления со значением -4Z₂. Теперь начинаем применять граничные условия. С помощью граничного условия (2.15) находим, что сопротивление Z₁ равно нулю на нулевой частоте. Это одна граничная частота. Вторую граничную частоту находим из условия (2.14), которая соответствует точке пересечения графика сопротивления Z₁ и графика сопротивления -4Z₂. Это частота . На рисунке 2.4 сплошной чертой по оси частот показана полоса пропускания этого фильтра.

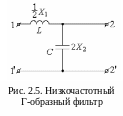О пределим поведение затухания в низкочастотном фильтре. Учитывая, что затухание в Т- образном и в П – образном фильтрах в два раза больше затухания в Г – образном фильтре, то рассмотрим затухание в низкочастотном Г - образном фильтре. На рисунке 2.5 представлена схема Г – образного фильтра с обозначением элементов так, как это принято было в формулах (2.16) – (2.24).

Для определения граничных частот понадобятся Z₁ и Z₂. Для этого используем обозначения рисунка 2.3,а:

.

Из условия (2.15) находим первую граничную частоту:

,

Из условия (2.14) находим вторую граничную частоту, она же частота среза:

, .

Перейдём к определению затухания фильтра. Для этого необходимо определить X₁ и X₂:

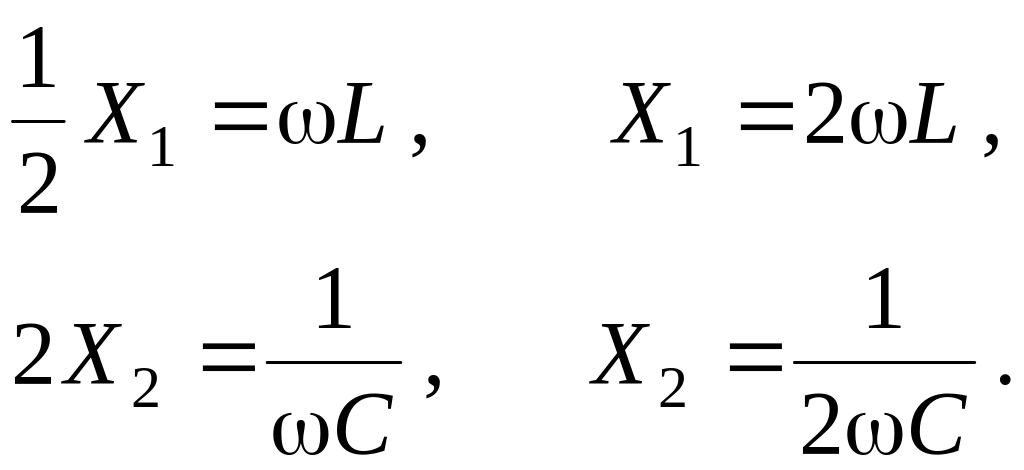(2.25)

Здесь в сопротивлении конденсатора опущен минус, т. к. он был учтен в (2.16).

С учетом (2.25) выражение (2.23) принимает в

. (2.26)

Из (2.24) с учетом (2.26) находим:

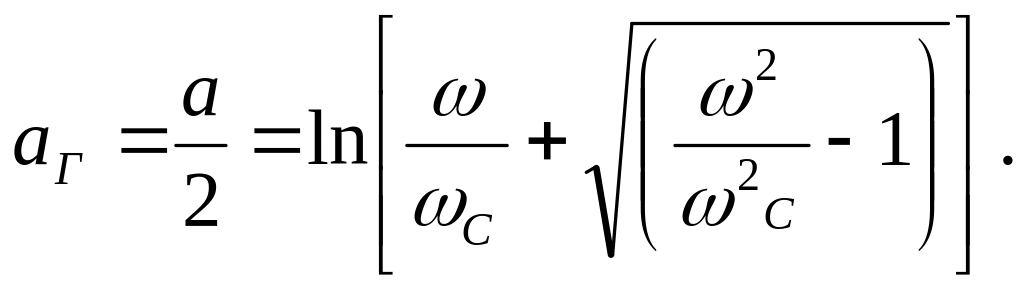(2.27)

На рис. 2.6 представлен вид зависимости (2.27) собственного затухания низкочастотного Г - образного фильтра.

Проанализируем (2.27). При ω=ω_C собственное затухание равно нулю. Слева от ω_C аргумент логарифма будет комплексным с модулем меньше единицы, что дает отрицательное значение затуханию. В этой области частот затухание считается равным нулю. Справа от ω_C собственное затухание возрастает по логарифмическому закону.

В заключении ещё раз отметим, что при вычислении затухания по (2.24) выражения для сопротивлений X₁ и X₂ берутся по модулю, так как знаки этих сопротивлений были учтены в (2.16), так же при переходе от (2.17) к (2.18).

Рассмотрим зависимость Z_T и Z_П от частоты для Г-образного низкочастотного фильтра (рис.2.3,а). Выразим Z₁ и Z₂ через параметры фильтра:

Подставляя найденные выражения для Z₁ и Z₂ в формулы Z_T и Z_П (2.3), находим:

. (2.28)

На рис. 2.7 показаны зависимости Z_Т и Z_П от частоты в области пропускания.

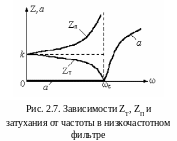
Видно, что в области пропускания входное и выходное сопротивления фильтра не постоянны при изменении частоты. Это не позволяет обеспечить согласованный режим его с нагрузкой во всем интервале пропускаемых частот и является одним из недостатков фильтров типа – k.

Высокочастотные фильтры.

На рис. 2.8 представлены схемы высокочастотных фильтров типа – k.

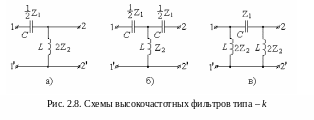
По схемным решениям на рисунке 2.8 представлены Г – образный фильтр (рис. 2.8,а), Т- образный фильтр (рис. 2.8,б) и П – образный фильтр (рис. 2.8,в).

Рассмотрим частотные свойства этих фильтров. Для этого необходимо, как и в низкочастотных фильтрах найти граничные частоты, определяющие полосу пропускания. Расположение полосы пропускания на оси частот покажет действительно ли эти фильтры являются высокочастотными.

Выполним частотный анализ для схемы рисунок 2.8,б. Находим для этой схемы сопротивления Z₁ и Z₂:

Из условия (2.14) находим одно граничное значение частоты полосы пропускания, она же частота среза:

.

Из условия (2.15) находим второе граничное значение частоты полосы пропускания:

Итак, полоса пропускания рассмотренного фильтра ограничивается некоторой частотой ω₁ и частотой ω₂, равной бесконечности. Значит, рассмотренная схема пропускает высокие частоты и является высокочастотным фильтром.

Н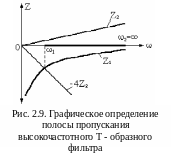 а рис. 2.9 показано графическое определение границ полосы пропускания рассмотренного высокочастотного фильтра. Вначале строим графики следующих сопротивлений: Z₁, Z₂, -4Z₂. Затем, используя граничное условие (2.14), находим частоту, соответствующую точке пересечения графиков сопротивлений Z₁ и -4Z₂. Это частота ω₁. Далее обращаемся к второму граничному условию (2.15) и находим, что Z₁ равняется нулю при частоте равной бесконечности. На рисунке 2.9 сплошной чертой по оси частот показана полоса пропускания этого фильтра, которая расположена в интервале от частоты ω₁ до частоты, равной бесконечности.

Определим затухания в высокочастотном фильтре. Учитывая, что затухание в Т- образном и в П – образном фильтрах в два раза больше затухания в Г – образном фильтре, то рассмотрим затухание в высокочастотном Г - образном фильтре (рис. 2.8,а). Последовательность анализа будет аналогична той, как при анализе низкочастотного фильтра.

Для определения граничных частот понадобятся Z₁ и Z₂. Из схемы рисунка 2.8,а находим:

; ; ; .

Из условия (2.14) находим первую граничную частоту, она же частота среза:

; ; .

Из условия (2.15) находим вторую граничную частоту:

,

Перейдём к определению затухания фильтра. Для этого необходимо определить X₁ и X₂:

; ; ; . (2.29)

Здесь в сопротивлении конденсатора опущен минус, т. к. он был учтен в (2.16).

С учетом (2.29) выражение (2.23) принимает вид:

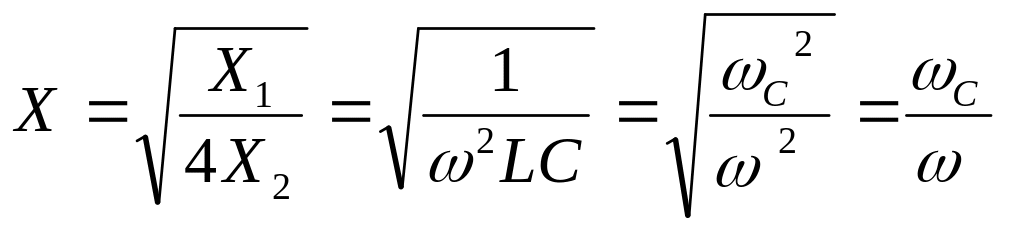. (2.30)

Из (2.24) с учетом (2.30) находим:

(2.31)

На рисунке 2.10,а представлена зависимость подавления высокочастотного фильтра от частоты. Проанализируем (2.31). При ω=ω_C собственное затухание равно нулю. Справа от ω_C (рис. 2.10,а), то есть когда частота сигнала больше частоты среза аргумент логарифма будет комплексным с модулем меньше единицы, что дает отрицательное значение затуханию. В этой области частот затухание считается равным нулю. Слева от ω_C (рис. 2.10,а), то есть когда частота сигнала меньше частоты среза собственное затухание возрастает по логарифмическому закону и стремится к бесконечности.

Зависимость характеристических сопротивлений Z_T и Z_П от частоты высокочастотного фильтра определяется подстановкой Z₁ и Z₂ в (2.3):

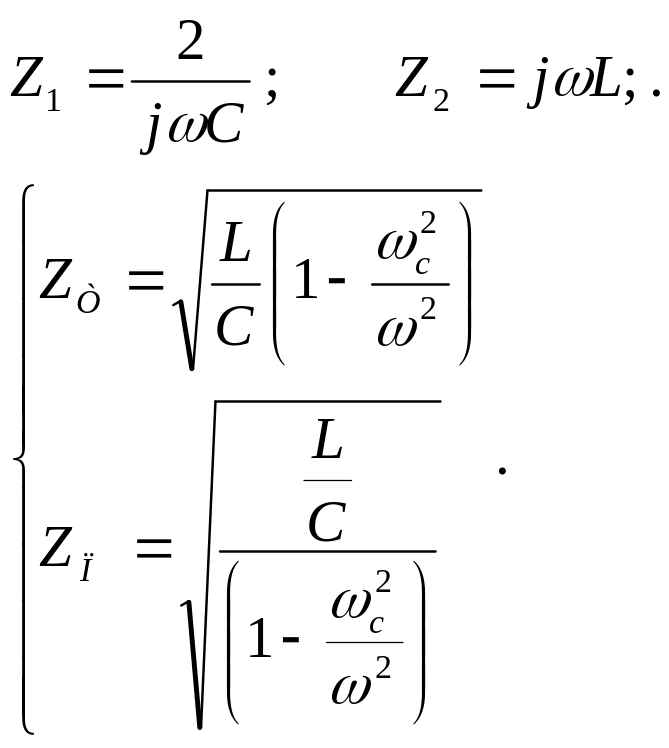(2.32)

На рис. 2.10,б показаны зависимости Z_T и Z_П (2.32) от частоты.

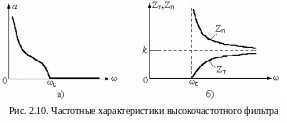
Видно, что в области пропускаемых частот входное и выходное сопротивления существенно зависят от частоты. Это значит, что согласованный режим может быть осуществлен только в узком интервале частот.

Полосовые фильтры

Рассмотрим полосовой фильтр типа – k, схемы которого представлены на рисунке 2.11. Как видно из схем, полосовые фильтры строятся на основе последовательных и параллельных резонансных контуров.

По схемным решениям на рисунке 2.11 представлены Г – образный фильтр (рис. 2.11,а), Т- образный фильтр (рис. 2.11,б) и П – образный фильтр (рис. 2.11,в).

Ч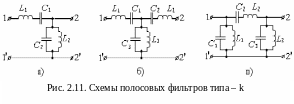 астотные свойства полосовых фильтров определяются частотными свойствами резонансных контуров. Как известно, последовательный контур на резонансной частоте имеет нулевое сопротивление, а параллельный контур на резонансной частоте имеет бесконечное сопротивление.

Оба контура в фильтре настроены на одну частоту, и на этой частоте последовательный контур представляет собой коротко замкнутую цепь, а параллельный контур представляет собой разрыв.

Н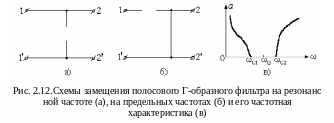 а рисунке 2.12,а показана эквивалентная схема Г-образного фильтра для этого режима. Из схемы видно, что выходное напряжение равно входному и, следовательно, подавление в этом случае равно нулю и выходной сигнал равен входному. Полоса пропускания фильтра определяется полосой пропускания резонансных контуров. Как известно из теории резонансных контуров , если последовательный и параллельный контура фильтра настроены на одну резонансную частоту и имеют одинаковую добротность, то полосы пропускания у них равны и будут определяться по известной формуле:

.

Эта же полоса пропускания может быть найдена с помощью экспериментально снятых амплитудночастотных характеристик для каждого контура. Частоты среза определяются, как граничные частоты полосы пропускания по известным формулам :

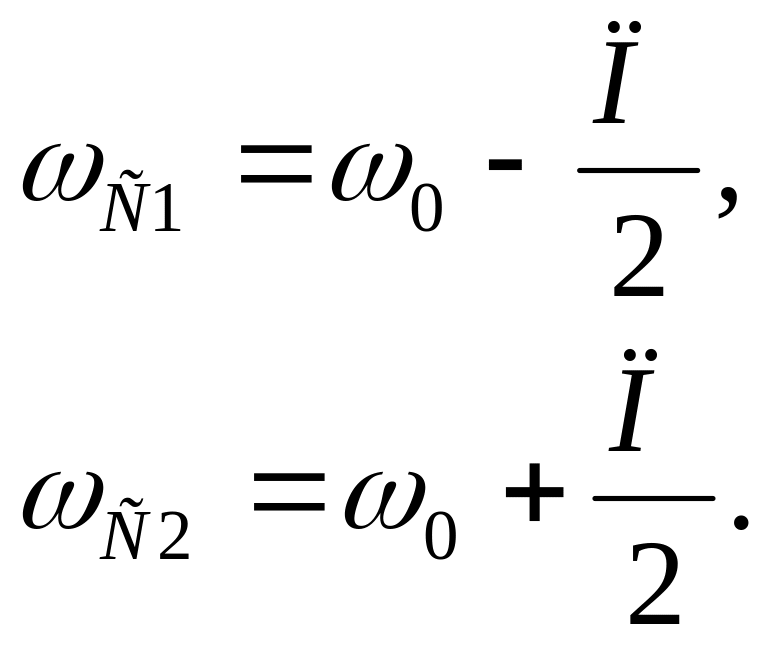
В области низких частот сопротивление последовательного контура высоко из-за наличия в нём последовательно включённого конденсатора, а в области высоких частот сопротивление последовательного контура так же высоко из-за наличия в нём последовательно включённой индуктивности. При ω=0 и ω= сопротивление последовательного контура равно бесконечности, что эквивалентно разрыву цепи. Сопротивление параллельного контура на низких частотах мало из-за наличия индуктивности, которая включена параллельно выходным выводам фильтра, что приводит к уменьшению выходного сигнала. На высоких частотах происходит так же подавление выходного сигнала за счёт малого сопротивления конденсатора параллельно включённого по отношению к выходным выводам фильтра. На предельных частотах (ω=0, ω=) сопротивление параллельного контура равно нулю, что соответствует короткому замыканию. Это отображено на рис. 2.12,б, где показана схема замещения Г-образного фильтра на предельных частотах. Видно, что в этих режимах выходное напряжение будет равно нулю. Это означает, что в этих режимах подавление схемы стремится к бесконечности. На рис. 2.12,в показана зависимость подавления от частоты полосового фильтра.

Режекторные фильтры.

Противоположностью полосового фильтра является режекторный фильтр. Он не пропускает сигналы в некотором интервале средних частот и пропускает сигналы на низких и высоких частотах.

Схемы режекторного фильтра типа – k представлены на рис. 2.13:

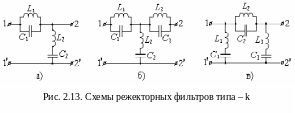
Как видно, режекторные фильтры отличаются от полосовых тем, что последовательные и параллельные контура поменялись местами. По схемным решениям на рисунке 2.13 представлены Г – образный фильтр (рис. 2.13,а), Т- образный фильтр (рис. 2.13,б) и П – образный фильтр (рис. 2.13,в).

Частотные свойства режекторных фильтров определяются так же частотными свойствами резонансных контуров. Как рассматривалось 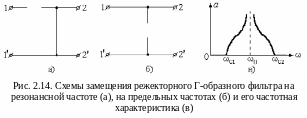раньше, на резонансной частоте параллельный контур имеет высокое сопротивление и теоретически, при отсутствии потерь в катушке индуктивности и конденсаторе, стремится к бесконечности . Сопротивление последовательного контура на резонансной частоте мало и, при отсутствии потерь в катушке индуктивности и конденсаторе, стремится к нулю . На рис.2.14,а показана эквивалентная схема Г-образного режекторного фильтра для резонансного режима. Видно, что в этом случае выходное напряжение равно нулю. Следовательно, в этом режиме подавление фильтра равно бесконечности.

Область подавления определяется частотами среза (ω_С1 и ω_С2), которые равны граничным частотам полосы пропускания параллельного контура. Как известно из теории резонансных контуров, при резонансе в параллельном контуре падение напряжения на контуре имеет максимальное значение . В нашем случае, в соответствии со вторым законом Кирхгофа, это приводит к уменьшению напряжения на выходных выводах, то есть подавлению сигнала. Сами частоты среза определяются аналогично тому, как это делается в полосовых фильтрах.

На низких и высоких частотах (за пределами полосы подавления) сопротивление параллельного контура уменьшается, а сопротивление последовательного контура растет. На предельных частотах (ω=0 и ω=) параллельный контур превращается в короткозамкнутый участок цепи, а последовательному контуру эквивалентен разрыв. На рисунке 2.14,б показана эквивалентная схема режекторного Г-образного фильтра на предельных частотах. Видно, что выходное напряжение будет равно входному, что соответствует нулевому подавлению входного сигнала. На (рис.2.14,в) показана зависимость подавления режекторного фильтра от частоты.

Положительные и отрицательные свойства фильтров типа – k.

Рассмотренные фильтры типа – k обладают как положительными, так и отрицательными свойствами. К положительным свойствам следует отнести их простоту схемного решения и возрастающий характер изменения подавления при удалении от частоты среза. Значительным недостатком этих фильтров является малая крутизна возрастания подавления за частотой среза. Это не обеспечивает достаточно глубокого подавления частот, находящихся вблизи от частоты среза в области подавления. Другим заметным недостатком фильтров типа – k является зависимость их характеристических сопротивлений от частоты. Это не позволяет обеспечить согласование фильтра с нагрузкой в значительной части полосы пропускания.

2.4. Фильтры типа – m

Фильтры типа – m свободны от основных недостатков фильтров типа – k. Это достигается усложнением схемного решения фильтров. Характер усложнения можно сформулировать так. В тех фильтрах типа – k, где в ветвях используются одиночные элементы, в фильтрах типа – m используется хотя бы один резонансный контур. В тех фильтрах типа – k, где используются одиночные контура, в фильтрах типа – m используются сложные контура.

Низкочастотные фильтры.

Н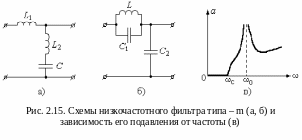 а рис. 2.15 представлены два варианта низкочастотных фильтров типа – m. Сравнивая их со схемой Г - образного низкочастотного фильтра типа – k (рис. 2.3,а), видим, что возможны два варианта построения Г - образного низкочастотного фильтра типа – m. Один вариант состоит в замене конденсатора последовательным резонансным контуром, резонансная частота которого больше частоты среза ( ). Как известно, на резонансной частоте последовательный контур имеет нулевое сопротивление, что эквивалентно появлению перемычки между выходными выводами фильтра. Это приводит к отсутствию сигнала на выходе, то есть полному подавлению входного сигнала. В свою очередь это значит, что подавление на этой частоте равно бесконечности.

На рисунке 2.15,в представлена зависимость подавления этого фильтра от частоты. Видно, что за счёт того, что подавление на резонансной частоте равно бесконечности крутизна нарастания подавления в интервале от частоты среза до резонансной частоты резко возросла. Очевидно, что чем ближе резонансная частота к частоте среза, тем круче нарастание подавления в этом интервале. Следует обратить внимание и на то, что за резонансной частотой на некотором интервале частот имеет место большое подавление, но, в то же время, подавление имеет ниспадающий характер при увеличении частоты. Последнее является не желательным явлением для фильтра. Частота среза определяется аналогично тому, как это делалось выше и равна:

где П – полоса пропускания последовательного резонансного контура.

Второй вариант построения Г - образного низкочастотного фильтра типа – m состоит, как видно из рисунка 2.15,б, в замене индуктивности в схеме Г - образного низкочастотного фильтра типа – k (Рис. 2.8,а) на параллельный резонансный контур. Резонансная частота этого контура больше частоты среза ( ). Как известно, на резонансной частоте сопротивление параллельного контура равно бесконечности, что эквивалентно появлению разрыва между входом и выходом фильтра. Это приводит к отсутствию сигнала на выходе на этой частоте, то есть полному подавлению входного сигнала. В свою очередь это означает, что подавление на этой частоте равно бесконечности. Рассмотренная выше зависимость подавления от частоты на рисунке 2.15,в так же отображает частотные свойства фильтра на рисунке 2.15,б. Всё сказанное выше относительно первого варианта низкочастотного типа – m (рис. 2.15,а) полностью соответствует второму варианту низкочастотного типа – m (рис. 2.15,б).

Высокочастотные фильтры.

На рисунке 2.16 представлены два варианта высокочастотных фильтров типа – m. Сравнивая их со схемой Г - образного высокочастотного фильтра типа – k (рис. 2.8,а), видим, что возможны два варианта построения Г - образного высокочастотного фильтра типа – m. Один вариант состоит в замене индуктивности последовательным резонансным контуром, резонансная частота которого меньше частоты среза ( ). Как известно, на резонансной частоте последовательный контур имеет нулевое сопротивление, что эквивалентно появлению перемычки между выходными выводами фильтра. Это приводит к отсутствию сигнала на выходе, то есть полному подавлению входного сигнала. В свою очередь это значит, что подавление на этой частоте равно бесконечности.

На рисунке 2.16,в представлена зависимость подавления этого фильтра от частоты. Видно, что за счёт того, что подавление на резонансной частоте равно бесконечности крутизна нарастания подавления в интервале от частоты среза до резонансной частоты резко возросла.

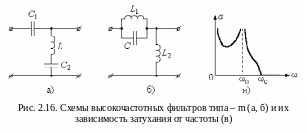
Очевидно, что чем ближе резонансная частота к частоте среза, тем круче нарастание подавления в этом интервале. Следует обратить внимание и на то, что за резонансной частотой на некотором интервале частот имеет место большое подавление, но, в то же время, подавление имеет ниспадающий характер на некотором интервале при уменьшении частоты. Последнее является не желательным явлением для фильтра. Частота среза определяется аналогично тому, как это делалось выше и равна:

где П – полоса пропускания последовательного резонансного контура.

Второй вариант построения Г - образного высокочастотного фильтра типа – m состоит, как видно из рисунка 2.16,б, в замене конденсатора в схеме Г - образного низкочастотного фильтра типа – k (Рис. 2.8,а) на параллельный резонансный контур. Резонансная частота этого контура меньше частоты среза ( ). Как известно, на резонансной частоте сопротивление параллельного контура равно бесконечности, что эквивалентно появлению разрыва между входом и выходом фильтра. Это приводит к отсутствию сигнала на выходе на этой частоте, то есть полному подавлению входного сигнала. В свою очередь это означает, что подавление на этой частоте равно бесконечности. Рассмотренная выше зависимость подавления от частоты на рисунке 2.16,в так же отображает частотные свойства фильтра на рисунке 2.16,б. Всё сказанное выше относительно первого варианта низкочастотного типа – m (рис. 2.16,а) полностью соответствует второму варианту низкочастотного типа – m (рис. 2.16,б).

Полосовые фильтры.

Выше было сказано, что фильтры типа – m получаются в результате усложнения схем фильтров типа – k и там, где используются одиночные контура, в фильтрах типа – m используются сложные контура. В фильтрах типа – k резонансные контура используются в полосовых и режекторных фильтрах.

Рассмотрим как строится полосовой фильтр типа – m. При построении полосового фильтра типа – m в схему полосового фильтра типа – k вводится дополнительный резонансный контур. На рис. 2.17а представлен вариант схемного решения Г – образного полосового фильтра типа – m. Здесь последовательно с параллельным контуром (рис. 2.11,а) включён последовательный резонансный контур. В полосовом фильтре ветвь из последовательно соединенных параллельного контура и последовательного контура создаёт два последовательных контура с различными резонансными частотами.

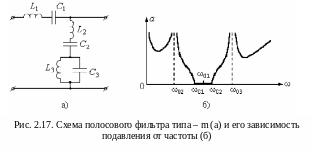
Один последовательный резонансный контур состоит из L₂-C₂-L₃ и имеет резонансную частоту ω₀₂:

Второй резонансный контур состоит из L₂-C₂-С₃ и имеет резонансную частоту ω₀₃:

где

На этих частотах ω₀₂ и ω₀₃ затухание фильтра стремится к бесконечности. Резонансная частота ω₀₁ последовательного контура L₁C₁ находится в полосе пропускания между частотами среза ω_C1 и ω_C2 и определяется по формуле:

.

Частоты среза определяются по выше приводимым формулам:

,

где П – полоса пропускания последовательного контура L₁-C₁.

При выборе элементов сложного контура необходимо обеспечить следующие условия:

, .

На рисунке 2.17,б показана зависимость подавления от частоты полосового фильтра типа – m. Из рисунка видно, что появление новой системы контуров с резонансными частотами и , удовлетворяющие выше указанным требованиям, увеличивают крутизну возрастания подавления за границами среза. Очевидно, что крутизна возрастания подавления тем больше, чем больше приближаются резонансные частоты сложной системы контуров к частотам среза.

Построение Т – образного и П – образного фильтров типа – m при известной схеме Г – образного фильтра не представляет труда и предлагается выполнить это самостоятельно.

Режекторные фильтры.

Режекторный фильтр типа – m строится на основе режекторного фильтра типа – k (рис.2.13,а). При этом параллельный контур сохраняется без изменения, а последовательный контур заменяется сложным контуром. Сложный контур состоит из последовательно соединённых параллельного контура и последовательного контура, аналогично тому, как это было сделано в схеме полосового фильтра (рис.2.17,а). Схема режекторного Г - образного фильтра типа – m представлена на рис. 2.18,а, а на рис. 2.18,б представлена зависимость его подавления от частоты.

Параллельный контур L₁ – C₁ имеет резонансную частоту :

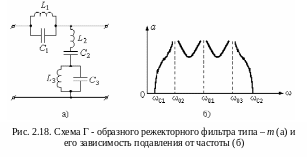
На резонансной частоте сопротивление параллельного контура стремится к бесконечности, что создаёт подавление, стремящееся к бесконечности.

Частоты среза определяются через резонансную частоту и полосу пропускания параллельного контура:

,

где П – полоса пропускания параллельного контура L₁-C₁.

Как и в полосовом фильтре, из двух последовательно включённых контура можно выделить два последовательных контура со своими резонансными частотами. Рассмотрим их ещё раз.

Один последовательный резонансный контур состоит из L₂-C₂-L₃ и имеет резонансную частоту ω₀₂:

Второй резонансный контур состоит из L₂-C₂-С₃ и имеет резонансную частоту ω₀₃:

где

На этих частотах ω₀₂ и ω₀₃ затухание фильтра стремится к бесконечности.

При выборе элементов сложного контура для режекторного фильтра необходимо обеспечить условия, отличающиеся от условий для полосового фильтра и которые состоят в следующих неравенствах:

, .

Из рисунка 2.18,б видно, что появление новой системы контуров с резонансными частотами и , удовлетворяющие выше указанным требованиям, увеличивают крутизну возрастания подавления за границами среза. Очевидно, что крутизна возрастания подавления тем больше, чем больше приближаются резонансные частоты сложной системы контуров к частотам среза.

Построение Т – образного и П – образного фильтров типа – m при известной схеме Г – образного фильтра не представляет труда и предлагается выполнить это самостоятельно.

Подводя итог рассмотрения фильтров типа – m можно сказать, что они имеют высокую крутизну изменения затухания от частоты в окрестности частоты среза. Следует отметить, что в этих фильтрах характеристические сопротивления в области полосы пропускания слабо зависят от частоты, что обеспечивает хорошее их согласование с входной цепью и выходной цепью в диапазоне пропускаемых частот.

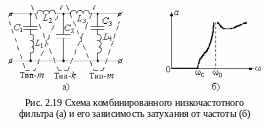Недостатком фильтров типа – m является уменьшение (провал) затухания в области подавления. Для устранения этого недостатка осуществляют каскадное включение фильтров типа – m и типа – k. На рисунке 2.19,а показана схема комбинированного низкочастотного фильтра, а на рисунке 2.19,б показана зависимость его подавления от частоты.

2.5. Безиндуктивные фильтры

Рассмотренные ранее фильтры состоят из реактивных элементов. На низких частотах (10 ÷ 30 кГц) размеры элементов фильтров становятся значительными, особенно у катушки индуктивности. Это затрудняет их применение в радиоаппаратуре по конструктивным соображениям, так как их размеры становятся соизмеримыми с размерами всего радиоустройства. В этих случаях применяются безиндуктивные фильтры. Они представляют собой в основе фильтр типа – k, в котором индуктивность заменена резистором. В этом случае фильтры содержат резистор и конденсатор, поэтому такие фильтры еще называют RC-фильтрами.

Низкочастотный фильтр.

Н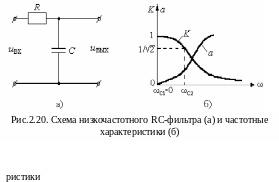 а рис. 2.20,а представлена схема низкочастотного Г - образного RC-фильтра. Рассмотрим частотные свойства этой схемы и выясним обладает ли она свойствами низкочастотного фильтра.

Определим амплитудно-частотную характеристику этого фильтра. Напомним, что под АЧХ четырёхполюсника понимается (5.26) модуль его комплексного коэффициента передачи по напряжению.

(2.33)

На рисунке 2.20,б представлена зависимость коэффициента передачи этого фильтра от частоты. Видим, что на нулевой частоте он равен единице, а с увеличением частоты уменьшается и стремится к нулю.

Определим затухание фильтра. В соответствии с (1.19) и пользуясь результатами (2.33), находим:

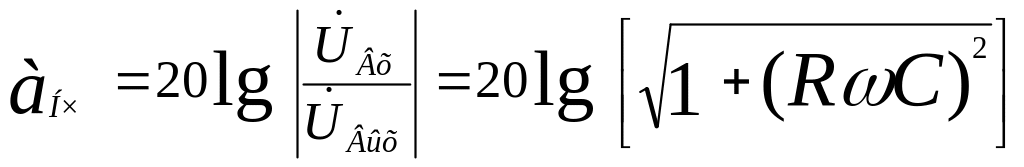(2.34)

На рисунке 2.20,б представлена зависимость подавления фильтра от частоты. Из графика видно, что на низких частотах подавление имеет малое значение, то есть на низких частотах сигнал будет пропускаться этим фильтром. На высоких частотах подавление фильтра растёт и стремится к бесконечности. Из сказанного следует, что рассматриваемая схема (рис.2.20,а) обладает свойствами низкочастотного фильтра.

Определим полосу пропускания этого фильтра. Одно значение граничной частоты полосы пропускания равно нулю (ω_C1=0). Второе значение граничной частоты полосы пропускания можно найти из понятия полосы пропускания, взяв уровень коэффициента неравномерности :

(2.35)

Из последнего соотношения следует, что на границе полосы пропускания сопротивления конденсатора и резистора равны:

(2.36)

С учетом (2.35) из (2.34) находим величину подавления на частоте, равной частоте :

Итак, низкочастотный фильтр пропускает сигнал в интервале от нулевой частоты до частоты (рис.2.20,б).

Высокочастотный фильтр.

На рисунке 2.21,а представлена схема высокочастотного RC-фильтра. Рассмотрим частотные свойства этой схемы и выясним обладает ли она свойствами высокочастотного фильтра.

Определим амплитудно-частотную характеристику этого фильтра. Она имеет вид:

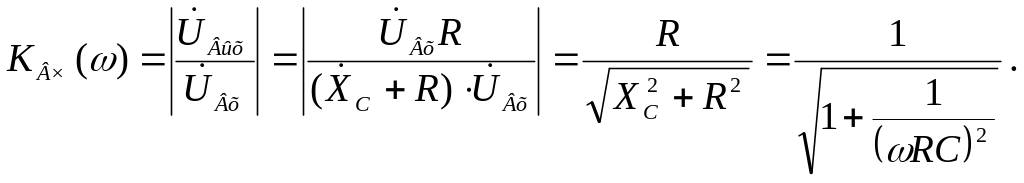(2.37)

На рисунке 2.21,б представлена зависимость коэффициента передачи этого фильтра от частоты. Видим, что на нулевой частоте он равен нулю, а с увеличением частоты увеличивается и стремится к единице.

Определим затухание фильтра. В соответствии с (1.19) и пользуясь результатами (2.37), находим:

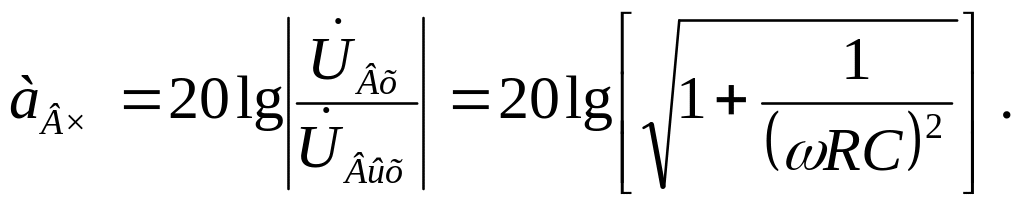(2.38)

Н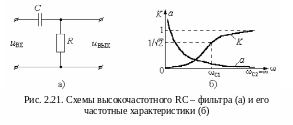 а рисунке 2.21,б представлена зависимость подавления фильтра от частоты. Из графика видно, что на низких частотах подавление имеет максимальное значение, то есть на низких частотах сигнал будет подавляться этим фильтром. На высоких частотах подавление фильтра мало и стремится к нулю. Из сказанного следует, что рассматриваемая схема (рис.2.21,а) обладает свойствами высокочастотного фильтра.

Определим полосу пропускания этого фильтра. Одно значение граничной частоты полосы пропускания равно бесконечности ( ). Второе значение граничной частоты полосы пропускания можно найти из понятия полосы пропускания, взяв уровень коэффициента неравномерности :

(2.39)

Из (2.39) видно, что на границе полосы пропускания ω_C1 сопротивление конденсатора равно сопротивлению резистора:

(2.40)

С учетом (2.39) из (2.38) находим величину подавления на частоте среза ω_C1:

.

Итак, высокочастотный фильтр пропускает сигнал от частоты до частоты, стремящейся к бесконечности (рис.2.21,б).

Полосовой фильтр.

Схема полосового RC-фильтра представлена на рис. 2.22,а. Как видно, он состоит из каскадного соединения высокочастотного и низкочастотного RC-фильтров.

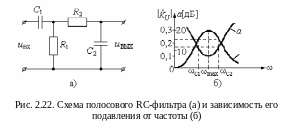
Принцип работы фильтра можно представить так. На нулевой частоте и на низких частотах сопротивление конденсатора С₁ высокое. Это приводит к большому падению напряжения на нём, что, в соответствии со вторым законом Кирхгофа, вызывает малое напряжения на выходных выводах фильтра. С увеличением частоты его сопротивление падает. При этом сопротивление конденсатора С₂ еще достаточно высоко, что создает на нем значительное падение напряжения, а значит приводит к наличию заметного напряжения на выходных выводах фильтра. Это соответствует режиму малого подавления входного сигнала. При дальнейшем увеличении частоты падает сопротивление конденсатора С₁, что уменьшает падение напряжения на нём. Однако, одновременно с этим уменьшается сопротивление конденсатора С₂, что ведёт к уменьшению падения напряжения на нём, а значит уменьшается напряжения на выходе фильтра. Дальнейшее увеличение частоты усиливает названный процесс, что ведёт к дальнейшему уменьшению выходного напряжения, а значит к увеличению подавляющего действия фильтра. На рисунке 2.22,б представлена зависимость подавления полосового RC-фильтра от частоты.

Проведём анализ полосового RC-фильтра. Входное сопротивление фильтра равно:

.

Найдём падение напряжения на резисторе R₁:

.

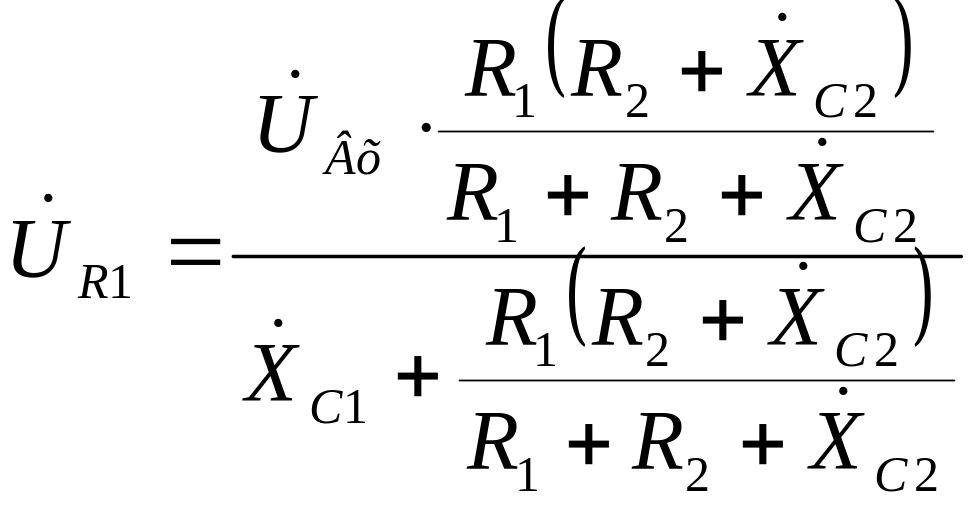Выходное напряжение определяется по формуле:

.

При построении полосовых фильтров часто выбираются элементы из следующих условий:

; .

С учётом последнего и выше полученных результатов, напряжение на выходе фильтра определяется по формуле:

.

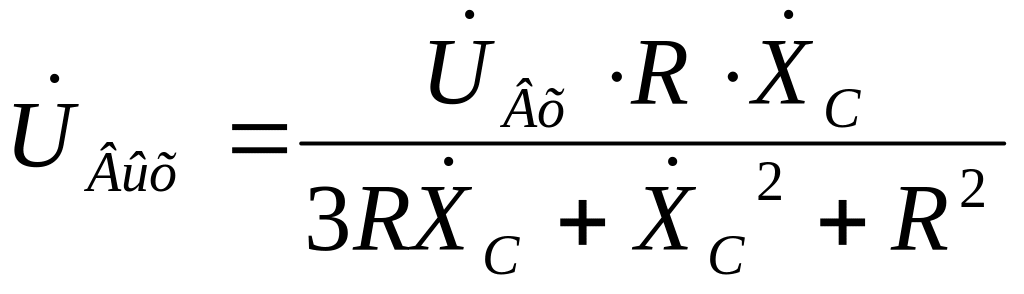Из последнего выражения находим коэффициент передача по напряжению в комплексной форме. После подстановки выражения для и очевидных преобразований, коэффициент передачи по напряжению полосового фильтра принимает вид:

.

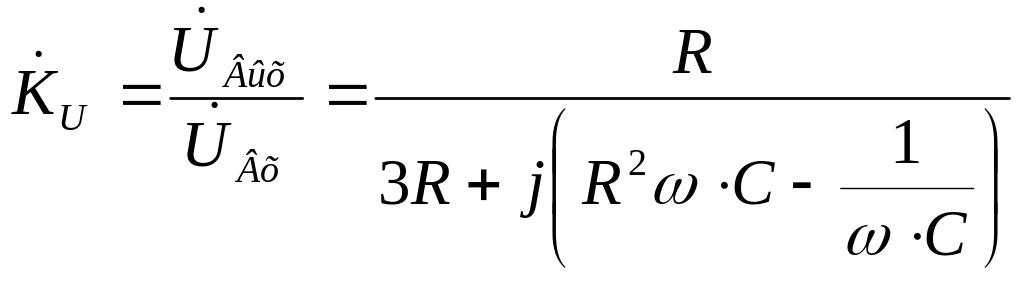Из коэффициента передача по напряжению в комплексной форме находим его модуль:

.

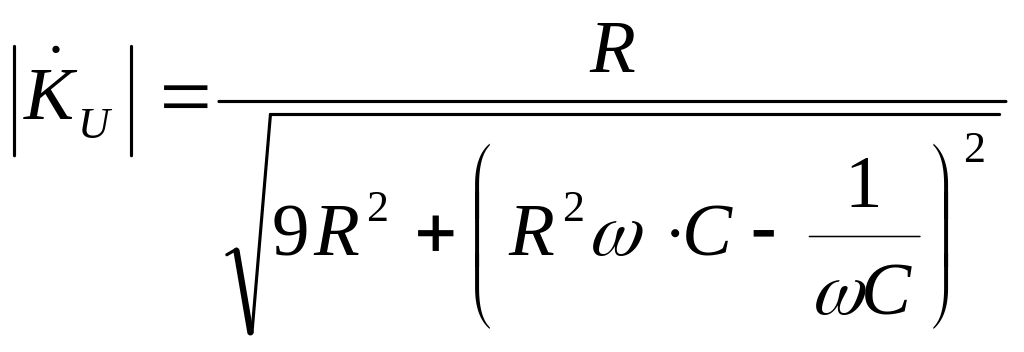Из полученного выражения видно, что на нулевой частоте и на частоте стремящейся к бесконечности коэффициент передачи по напряжению равен нулю. Очевидно, что внутри частотного интервала коэффициент передачи имеет некоторое максимальное значение. Можно исследовать это выражение на экстремум. Однако из формулы видно, что коэффициент передачи будет иметь максимальное значение, когда круглая скобка в знаменателе будет равна нулю:

.

Решая это уравнение относительно , находим частоту, на которой коэффициент передачи по напряжению имеет максимальное значение и которую обозначим, как :

.

Найдём чему равно максимальное значение коэффициента передачи на этой частоте, для чего подставим значение этой частоты в выражение для модуля коэффициента передачи по напряжению:

.

На рисунке 2.22,б показана зависимость модуля коэффициента передачи по напряжению фильтра от частоты.

Величина подавления на частоте равна:

.

Найдём частоты среза полосы пропускания полосового фильтра. Поступим аналогично тому, как это делалось раньше. Потребуем, чтобы на частотах среза выполнялось следующее условие:

.

Приравняем выражение для модуля коэффициента передачи по напряжению к полученному значению:

.

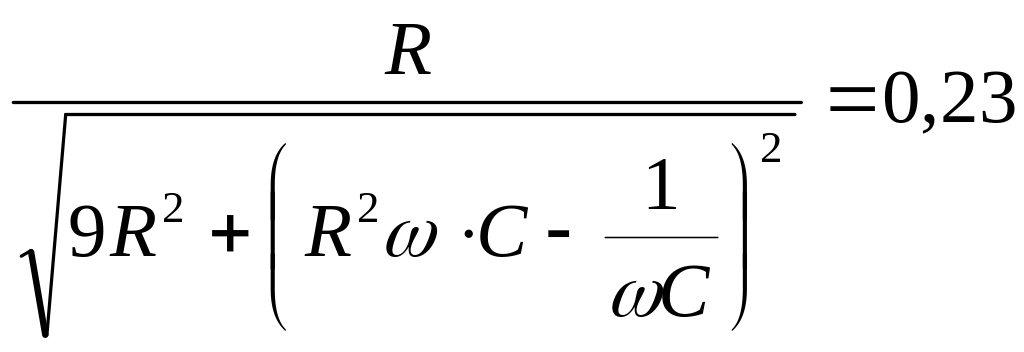В процессе решения этого уравнения относительно частоты получаем биквадратное уравнение и при извлечении квадратного корня берём только положительные значения. В результате находим следующие значения частот среза:

; .

Зная частоты среза, легко находим полосу пропускания полосового фильтра:

.

Подавление на частотах среза будет равно:

.

Итак, полосовой фильтр пропускает сигнал в интервале от частоты до частоты (рис.2.22,б).

Режекторные фильтры.

На рисунке 2.23,а представлена схема режекторного RC-фильтра. Как видно он состоит из параллельно соединённых Т - образного RC-фильтра низкой частоты (R₁, C₂, R₃) и Т – образного RC-фильтра высокой частоты (C₁, R₂, C₃).

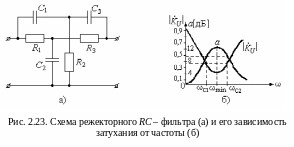
Проведём анализ режектороного фильтра. Элементы каждого из фильтров соединены звездой. Для проведения электрического анализа фильтра необходимо элементы соединённые звездой заменить на элементы соединённые треугольником . При построении режекторных фильтров, как правило, выполняются следующие условия:

R₁=R₂=R₃=R; C_1`=C₂=C₃=C.

В результате расчёта преобразованной схемы методом эквивалентного преобразования не трудно получить выражение для коэффициента передачи по напряжению в комплексной форме:

.

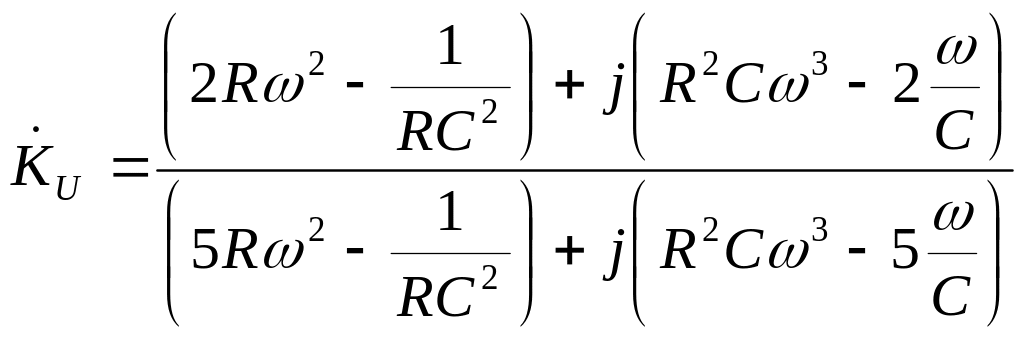Находим модуль комплексного коэффициента передачи, как модуль числителя делённого на модуль знаменателя. После раскрытия скобок и некоторых очевидных преобразований, получим:

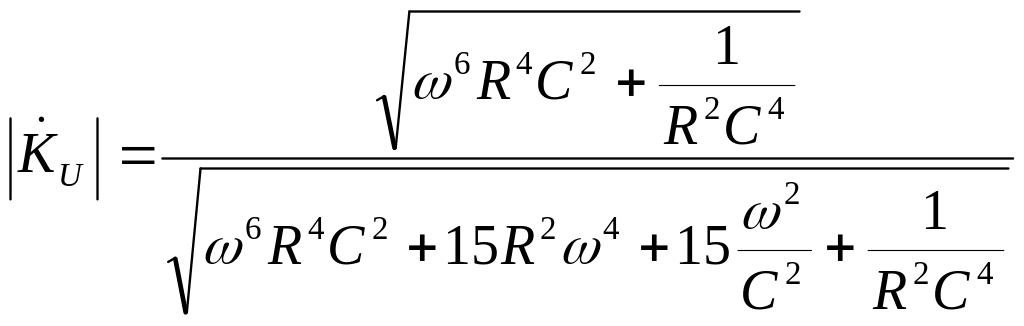. (2.41)

Из этого выражения видно, что при нулевой частоте коэффициент передачи равен единице:

.

Разделим числитель и знаменатель выражения (2.41) на :

.

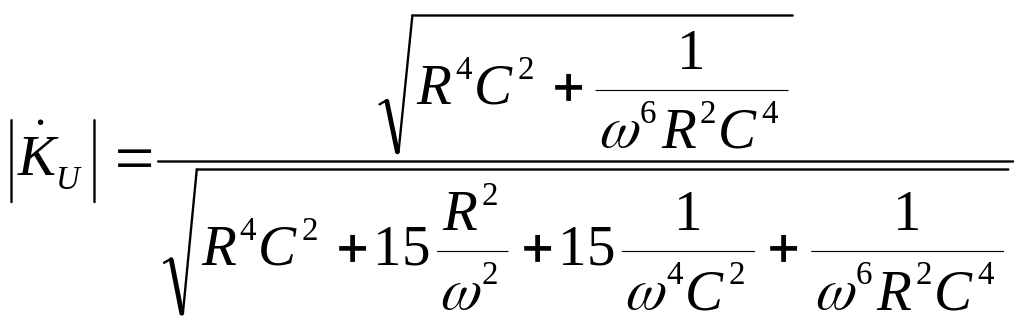Из этого выражения видно, что при стремлении частоты к бесконечности коэффициент передачи будет стремится к единице:

.

К таким же результатам можно прийти, если выполнить схемы замещения режекторного фильтра для этих крайних частот (0 и ). Предлагается это выполнить самостоятельно.

Рассмотрим физические процессы в режекторном фильтре. На нулевой частоте сопротивление конденсаторов равно бесконечности и всё входное напряжение передаётся на выходные выводы без потерь, так как на рисунке 2.23,а представлен фильтр в режиме холостого хода. На частоте близкой к бесконечности сопротивление конденсаторов практически равно нулю и входной вывод через перемычку, создаваемую конденсаторами С₁ и С₃, соединяется с выходным выводом. В этих случаях коэффициент передачи равен единице, подавление равно нулю. На промежуточных частотах по элементам фильтра протекает ток, что создаёт падение напряжения на его элементах. Это приводит к тому, что напряжение на выходе будет меньше входного, то есть будут проявляться подавляющие свойства фильтра. На некоторой частоте коэффициент передачи будет иметь минимальное значение. Выполняя исследование на экстремум выражение (2.41) и осуществляя некоторые упрощения в вычислениях, эта частота, которую обозначим как , имеет значение:

.

Найдём значение коэффициента передачи на этой частоте, для чего подставим её значение в (2.41):

.

Подавление на этой частоте будет равно:

.

На рисунке 2.23,б представлены графики коэффициента передачи и затухания. Для определения частот среза и полосы пропускания необходимо знать значение коэффициента передачи на границах полосы пропускания. В соответствии с трактовкой понятия полосы пропускания значение коэффициента передачи на границах полосы пропускания будет больше в раз значения коэффициента передачи на :

.

Откладывая это значение на оси коэффициента передачи, находим графически частоты среза (рис.2.23,б).

Подавление на частотах среза равно:

.

Итак, режекторный фильтр пропускает сигнал в следующих интервалах частот – от нулевой частоты до частоты и от частоты до частоты, стремящейся к бесконечности (рис.2.23,б).

2.6. Контрольные вопросы

Для проверки степени усвоения материалов главы 2 рекомендуется ответить на ниже предлагаемые вопросы. Свои ответы сравните с ответами, приведёнными в конце этих вопросов.

1. Два двухполюсника являются взаимообратимыми, если произведение их сопротивлений ……… от частоты.

А. Зависит. Б. Не зависит.

2. Для фильтров типа – k характерна ………. крутизна возрастания подавления за частотой среза.

А. Малая. Б. Большая.

3. Для фильтров типа – k характерна ……. характеристического сопротивления от частоты.

А. Зависимость. Б. Не зависимость.

4. Для фильтров типа – m характерна ………. крутизна возрастания подавления за частотой среза.

А. Малая. Б. Большая.

5. Для фильтров типа – m характерна ……… характеристического сопротивления от частоты.

А. Зависимость. Б. Не зависимость.

6. У фильтра типа – m проявляется ……… затухания в области подавления.

А. Не зависимость. Б. Уменьшение. В. Повышение.

7. Какое из названных свойств характерно для RC-фильтра.

А. Высокая крутизна подавления. Б. Не зависимость входного сопротивления от частоты. В. Малые размеры и вес.

Правильные ответы:

1. Б. 2.А. 3. А. 4. Б. 5.Б. 6. Б. 7. В.