методички / 4037

Кроме того, так как

2 = = 0

12 ,

где T0 = QH – энергия ударяющего тела к моменту начала удара, то выражение для динамического коэффициента может быть представлено еще и в таком виде:

Kд = 1 + √1 +	0	.	(12)

Если мы в формулах (8) и (9) положим H=0, т.е. просто сразу приложим груз Q, то δд = 2δ и Pд = 2P ; при внезапном приложении силы Q деформации и напряжения вдвое больше, чем при статическом действии той же силы.

Наоборот, если высота падения груза Н (или скоростьV) велика по сравнению с деформацией δ , то в подкоренном выражении формул (8)–(14) можно пренебречь единицей по сравнению с величиной отношения 2 /δ . Тогда для δд и Pд получаются следующие выражения:

δд = δ (1 + √1 +	2		) и Рд		= Р (1 + √1 +			2	) .	(13)
	δ							δ
При очень большой величине отношения 2 /δ можно пренебречь и единицей,
стоящей перед корнем, т.е. написать:
δд = δ √		2		и	Рд = Р √	2	.			(14)
		δ				δ

Динамический коэффициент в этом случае определяется по формуле

К	= √	2		= √	0	.	(15)
д		δ
Необходимо отметить, что в то время как пренебрежение единицей 2Н в
подкоренном выражении допустимо уже	при 2 /δ				≥ 10 (неточность приближенных

формул будет не больше 5 %). Пренебрежение единицей, стоящей перед корнем, допустимо лишь при очень большой величине отношения 2 /δ .

Так, например, для того чтобы приближенные формулы (14) и (15) давали погрешность не более 10%, отношение 2 /δ должно быть больше 110.

11

Формулы δд = Кдδ и Рд = КдР , в которых Кд выражается через Т0/Uc, могут быть использованы также для решения задачи о встречном ударе тел, двигающихся с некоторой скоростью. На этом основании их можно считать общими формулами для расчета на удар.

Обобщая сказанное выше, можем наметить следующий общий прием решения задач на определение напряжений при ударе. Применяя закон сохранения энергии, надо:

1)вычислить кинетическую энергию ударяющего тела Т;

2)вычислить потенциальную энергию Uд тел, воспринимающих удар, под нагрузкой их силами инерции при ударе; потенциальная энергия должна быть выражена через напряжение (σд, τд ) в каком-либо сечении, через деформацию (удлинение, прогиб) или через силу инерции Pд ударяющего тела;

3)приравнять величины Uд и Т и из полученного уравнения найти или непосредственно динамическое напряжение, или деформацию, а по ней, пользуясь законом Гука, напряжение или силу Pд и соответствующие ей динамические напряжения

идеформации.

Практическая работа № 3

РАСЧЕТ КРУГОВОЙ И ТЕХНИЧЕСКОЙ ЧАСТОТЫ, ПЕРИОДА ДЛЯ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ РАМЫ ЧЕРЕЗ КОЭФФИЦИЕНТ

ПОДАТЛИВОСТИ

Расчет балок и рам с сосредоточенными массами, имеющих несколько динамических степеней свободы на вибрационную нагрузку P = Psinθt (или P = Psinθt) обычно состоит из решения трех задач динамики.

1. Расчет на собственные колебания (1-я задача динамики) состоит из определения частот и форм собственных колебаний динамической системы. Для этого необходимо:

–выбрать расчетную схему и массовую модель сооружения;

–определить степени свободы сосредоточенных масс и их число n;

–определить величины масс, участвующих в колебаниях по каждой степени свободы

ипостроить диагональную матрицу масс m; для системы с двумя степенями свободы она имеет вид:

	= | 1	0 ];	(1)
(2х2)	0	2

–рассмотреть единичные загружения от воздействия единичных сил;

–во всех единичных загружениях построить эпюры моментов;

–вычислить податливости δij =Mi х Mj (i, j = 1, n) и построить квадратную матрицу податливости δ; для системы с двумя степенями свободы она имеет вид:

	δ	=	δ11	δ12	;	(2)
	(2х2)		δ21	δ22

12

– решить вековое уравнение − = 0 (где d=δm – динамическая матрица, E − единичная матрица) и вычислить собственные значения li, затем круговые частоты собственных колебаний ω; при необходимости можно определить формы собственных колебаний.

Для системы с одной динамической степенью свободы круговую (циклическую) частоту собственных колебаний можно определять по одной из формул:

ω=√	1	= √		= √		,	(3)
					ст

где m − величина сосредоточенной массы, δ, r − податливость и жесткость в направлении степени свободы, g − ускорение свободного падения, yст − статический прогиб точки от действия веса сосредоточенной массы.

2. Проверка на резонанс (2-я задача динамики) состоит из проверки условий

− 1 ≥ 0,3. Если во всех случаях результат ≥0,3, то резонанса нет и можно ограничиться

1

расчетом на статическое воздействие нагрузки; если хотя бы в одном случае результат <0,3, то динамический расчет надо продолжить.

3. Проверка динамической прочности (3-я задача динамики) состоит из проверки

условия прочности доп = доп < [ доп]. При длительном воздействии вибрационной нагрузки (более 110 циклов) за допустимое динамическое напряжение принимается доля допустимого статического напряжения: [ доп] = 14 ÷ 13 [ ст].

Для построения динамической эпюры моментов Мдоп необходимо:

–построить вектор амплитуд действующей на массы нагрузки Р;

–пользуясь единичными эпюрами от единичных загружений, построить грузовую эпюру MP от вектора нагрузки Р;

–вычислить все коэффициенты δ11 = δ11 − 1/ 2;

–вычислить вектор статического прогиба yст=δР;

–решить систему канонических уравнений расчета на вибрационную нагрузку; для системы с двумя степенями свободы эта система уравнений имеет вид:

δ11 1 + δ12 2 = 1,ст	;
{δ21 1 + δ22 2 = 2,ст		(4)

из которой определяются максимальные инерционные силы J1, J2;

–определить обобщенные силы Qi=Pi–Ji;

–построить эпюру динамических моментов от действия обобщенных сил Qi по формуле

Мдоп=Σ MiQi ,

(5)

13

из которой определить значение максимального момента доп и затем проверить условие прочности.

Для системы с одной динамической степенью свободы эпюру динамических моментов можно строить по формуле

Мдоп = μ·Mст ,

(6)

1

где μ=( / )2−1 – динамический коэффициент.

4. Проверка динамической жесткости (4-я задача динамики) решается при необходимости. Она состоит в проверке условия удоп ≤ [удоп]. Максимальные перемещения по направлениям степеней свободы масс при их колебаниях вычисляются по формуле

	= –		.	(7)
		2

В данной работе динамическая жесткость проверяется по табл. 1, где даны предельные значения допустимых амплитуд вибраций a (в зависимости от частоты вибраций f), действующих на человека в течение восьмичасовой рабочей смены в производственных условиях.

						Таблица 1
	Предельные значения допустимых амплитуд
f, Гц	2	5	10	20	40	80
a, мм	1,28	0,16	0,045	0,0225	0,0113	0,0056

Пример. На стальной балке находится работающий двигатель весом G = 200 кг (рис. 1, а), создающий при N = 2000 об/мин вибрационную нагрузку с амплитудой P0 = 10 кг. Решить четыре задачи динамики при следующих данных: балка двутавр № 60 с моментом инерции I = 76806 см4 и моментом сопротивления изгибу W = 2560 см3, модуль упругости стали E = 2×106 кг/см2, допустимое напряжение [ϭ] = 1600 кг/см2.

Решение. Вначале представим исходные данные в системе СИ:

P0 = 98 Н; G = 1960 Н; E = 19,6×1010 Н/м2; I = 7,68×10–4 м4; W = 2,56×10–3 м3;

[s]= 1,57×108 Н/м2.

1.Решаем 1-ю задачу динамики − находим частоту собственных колебаний.

Пренебрежение размерами двигателя, массой балки и ее продольными колебаниями позволяет определять положение груза (двигателя) при ее малых вертикальных колебаниях только одним вертикальным перемещением. Поэтому принимаем, что данная система является динамической системой с одной степенью свободы.

14

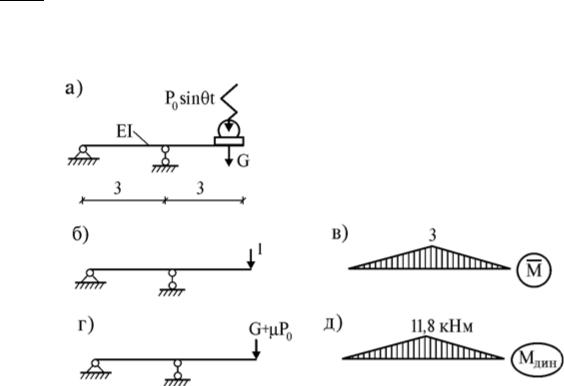
Тогда круговую частоту собственных колебаний можно вычислять по формуле ω = √ / ст, где статический прогиб yст находится из рассмотрения единичного загружения (рис. 1, б) и построения в нем единичной эпюры M (рис. 1, в). Имеем:

Рис. 1. Расчетные схемы и эпюры моментов

Тогда δ=Σ ∫

2

=

1

· 3 · 3 ·

2

· 3 ·

1

· 2 =

18

=

18

= 1,19 · 10−7.

2

3

10

−4

19,6·10

·7,68·10

ω=√

= √

=√

9.8

=204,5 (c–1).

·

1960·1,19·10−7

ст

2. Для решения 2-й задачи динамики (проверки системы на резонанс) вычислим круговую частоту вращения двигателя:

		=			=		3,14·2000	= 209,4 (c–1).
				30			30
Тогда	|	−	| = |			209,4−204,5			| = 0,024 < 0,3.
						204,5

Следовательно, колебания системы происходят в резонансно-опасной зоне. В этом случае необходимо решать следующие две задачи динамики, т. к. возможны большие напряжения и амплитуды колебаний.

3. Решаем 3-ю задачи динамики − проверяем систему на прочность. Для этого вычислим динамический коэффициент:

μ=	1	=	1	= 20,58.
	( / )2−1		1,0242−1

15

Максимальная сила, действующая на балку, будет равна сумме веса двигателя G и вибрационной силы Р0, сведенной к статической силе с использованием динамического коэффициента (рис. 1, г). Поэтому эпюру изгибающих моментов (рис. 1, д) можно построить по формуле

Мдоп = (G + μP0)M .

(8)

Максимальное напряжение в балке будет:

=

(G+μ )

(1960+20,58·98)·3

= 4,66 · 106

0

=

(Н/м2).

2,56·10−3

доп

Если принять [

] =

1

[

] =

1

· 1,57 · 108 = 5,23 · 107 (Н/м2),

доп

3

ст

3

то условие прочности выполняется:

< [ ].

доп

доп

4. Решим 4-ю задачу динамики − проверим систему на жесткость. Предполагая, что максимальная амплитуда колебаний будет в конце консоли при действии силы Р0, получим:

вибр = уст = 0 =20,58·98·1,19·10–7=2,4·10–4 (м)=0,24 (мм).

Так как частота вращения двигателя f = N/60 = 2000/60 = 33,3 (Гц), то из табл. 1 следует, что при данной частоте амплитуда колебаний превышает допустимую:вибр > [ доп] = 0,0113 . Значит, присутствие человека рядом с работающим двигателем недопустимо.

Практическая работа № 4

РАСЧЕТ ДВИЖЕНИЯ СИСТЕМЫ ПРИ ЗАДАННОМ НАЧАЛЬНОМ ВОЗМУЩЕНИИ

Вынужденные колебания рамного каркаса: метод разложения по формам собственных колебаний

Вынужденные колебания зависят от параметров колеблющейся системы и характеристик возмущающего воздействия.

Когда для упрощения задач отказываются от учета затухания колебаний, системы рассматривают как идеализированные и называют консервативными в отличие от реальных диссипативных систем. Сначала рассмотрим формальный расчет системы с конечным числом степеней свободы на действие сейсмических инерционных сил, с

16

использованием метода разложения по формам собственных колебаний. Уравнение движения системы можно записать как:

							̈		̇							(1)
					[M] { }+[C]{ }+[K]{U}= –[M]{1} ̈(t),
где
							11	12		1			1
											1
							21	22		2		0	2
											2
									0
					[K]=							0		,
							1	2	0
												0
						[	1	2						]
	1 + 2			− 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
	−	2	2 + 3		− 3			0			0 0 0 0 0
				− 3	+			−			0 0 0 0 0
	0
[K]=					3		4	4
	0			0		0		0	−		+		− + 1 0			0
				0
[ 0				0		0		0		0	0		0		0 ]

матрица жесткости системы, а матрица масс и матрица демпфирования имеет следующий вид:

		1	0	0	0		0	0				1 0		0	0	0	0
		0	2 0 0 0					0				0	2 0 0 0 0
[M] =		0	0	0			0	0			, [C] =	0	0	0		0	0
		0	0	0			0	0				0	0	0		0	0
		0	0	0	0		0					0	0	0	0	0
	[	0	0	0	0		0			]	[	0	0	0	0	0	]

Векторы перемещений, скорости и ускорений:

			1̇		1̈		1
	1		2̇		2̈
	2						1
{U} =		̇		̈		{1} =
		{ } =	̇	{ } =	̈		1
	{ }						{1}
			{ ̇}		{ ̈}

Здесь учтем, что для любых форм колебаний {ф}m и {ф}n (m≠n) справедливы условия ортогональности собственных форм колебаний:

{фm}T [M] {фn}= 0;

{фm}T [K] {фn}= 0 (m≠n).

(2)

17

Для m = n, получаем

{фm}T [M] {фn}= Mn;

	{фm}T [K] {фn}= Kn		(m = n).			(3)
	Модальная матрица:
		ф11		ф1		ф1
	[Ф] = [{ф1}{ф2} {ф } {фn}]=	ф21		ф2		ф2
			ф21		ф21
	[ф1			ф		ф ]

Допустим, что существует такое линейное преобразование:

{U} = [Ф] {Y}.

(4)

Подставляя уравнение (3) в уравнение (1) получим:

[М ][Ф]{ ̈} +[C] [Ф]{ ̇} + [ ][Ф]{ } = −[M]{1} ̈(t).

Умножая это уравнение слева на матрицу [Ф]T , получим:

[Ф]	T	̈	T	̇			[M]{1} ̈(t) .	(5)
		[М ][Ф]{ } +[Ф]		[C] [Ф]{ } + [Ф]		[ ][Ф]{ } = −[Ф]

Матричное уравнение (5) представляет собой систему несвязанных уравнений относительно обобщенной координате Yn. Используя условия ортогональности (5), получаем:

Мn ̈+Cn ̇+ = −[Ф] [M]{1} ̈(t)

или

̈+2ξnωn ̇+ 2			= −Г		̈(t),	(6)

где

{ф} [ ]{1}

Гn = {ф} [ ]{ф} n = 1,2…n (7)

– фактор влияния форм колебаний.

Пример. Для расчета динамической реакции нашей модели будем пользоваться спектральной теорией сейсмостойкости. Предположим, что спектр ускорений основания задаётся следующим графиком (ξ = 0,05).

18

Специально для нашей системы с тремя степенями свободы при затухании ξ = 0,05 имеем следующие спектральные данные:

SA1(0,05; 1,061) = 0,942 м/с2; SA2(0,05; 0,495) =2 м/с2; SA3(0,05; 0,334) = 2 м/с2.

Максимальные горизонтальные перемещения каркаса по формам колебаний:

			{ф} [ ]{1}													1		0,942			0,0115
{U}
	= {ф}			1					∙			1			= {2,15} ∙ 0,429 ∙					{Г={0,0246} [м],
														2					2
1	1		{ф}		[ ]{ф}													5,92
				1										1
							1									3,31					0,0379
			{ф}2				[ ]{1}						2			1				2	0,0044
{U}	= {ф}									∙						= { 0,89 }	∙ 0,353 ∙					{Г={ 0,0039 } [м],
		2 {ф}											22
2						[ ]{ф}										−1,46			12,692			−0,0064
				2			2
			{ф}3				[ ]{1}						3			1				2	0,0013
{U}	= {ф}	3								∙						= {−1,04}	∙ 0,224 ∙				{Г={−0,0013} [м].
															2					2
3						[ ]{ф}
			{ф}										3			0,41			18,81		0,0005
				3			3

Максимальное перемещение каркаса, считая влияние всех трех форм колебаний:

0,01152	0,00442	0,00132	0,0124
{U}max =√[{0,02462	} + { 0,00392	} + {−0,00132}] ={0,0249} [м].
0,03792	−0,00642	0,00052	0,0384

Инерционные сейсмические усилия на уровне этажей получаются с использованием следующих формул:

{F}			200		0	0	1	80,8
	= [ ]{ф} Г		= [	0	150	0 ] {2,15} ∙ 0,429 ∙ 0,942 = {130,3} [кН],
1	1 1 1
				0	0	100	3,31	133,8
{F}				200	0	0	1	141,2
	= [ ]{ф}	Г	= [	0	150	0	] { 0,89 } ∙ 0,353 ∙ 2 = {	94,3 } [кН],
2		2 2 2
				0	0	100	−1,46	−103,1
{F}				200	0	0	1	89,6
	= [ ]{ф}	Г	= [	0	150	0	] {−1,04} ∙ 0,224 ∙ 2 = {−69,9} [кН].
3		3 3 3
				0	0	100	0,41	18,4

Усилия на основание здания по формам колебаний:

1 = 80,8 +130,3 +133,8 = 349,9 кН,2 = 141,2 + 94,3 –103,1 = 132,4 кН,3 = 89,6 – 69,9 +18,4 = 38,1 кН.

19

Результатный вектор усилий по этажам:

185,7

{F}S = √({F}1)2 + ({F}2)2 + ({F}3)2 = {175,4} [кН]. 169,9

Результатное усилие основания:

TS =√(344,9)2 + (132,4)2 + (38,1)2 = 371,4 [кН].

Таким образом, метод разложения по собственным формам колебаний в комбинации с использованием спектральной теории сейсмостойкого строительства имеет большое прикладное значение для динамического расчета конструкций.

Практическая работа № 5

ДИНАМИЧЕСКИЙ РАСЧЕТ РАМЫ НА СИЛОВОЕ ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ С ПРОВЕРКОЙ ПРОЧНОСТИ

На раме с размерами, указанными на рис. 1, в точках 1 и 2 установлены два одинаковых вибратора весом G = 20 кН каждый и весом неуравновешенных частей Р0 = 1,2 кН, размещенные на оси вращения с эксцентриситетом е = 0,015 м. Вибраторы вращаются синфазно с частотой n = 600 об/мин.

Рама выполнена из двух двутавров № 50 (ГОСТ 8239 72), т.е. Jx = 3.29·10-4 м4; Wx = 0,157 10–2 м3. Рама изготовлена из стали с характеристиками Е = 2,1·105 МПа,

R = 190 МПа.

Пренебрегая собственным весом рамы и внутренним трением материала, требуется:

1.Составить канонические уравнения по методу сил, определяющие свободные колебания рамы, и получить значения частот и периодов собственных колебаний рамы;

2.Вычислить отношения амплитуд и графически изобразить возможные формы собственных колебаний рамы;

3.Проверить ортогональность собственных форм колебаний системы;

4.Определить круговую частоту вынужденных колебаний и изобразить примерный вид графика коэффициента динамичности;

5.Составить канонические уравнения по методу сил, определяющие вынужденные колебания системы, и определить амплитудные значения инерционных сил;

6.Построить статическую эпюру изгибающих моментов от всех вибраторов и эпюру амплитудных значений изгибающих моментов при вынужденном режиме колебания рамы;

7.Построить эпюру моментов при одновременном действии статических и динамических сил и определить положение опасного сечения конструкции;

20