2. Характеристики импульсного элемента. Гребенка δ-функции. Ее частотный спектр. Временная характеристика.

Характеристики импульсов и импульсной модуляции:

Длительность импульса τ – сигнал, который описывается функцией, не обращающейся в нуль только на некотором конечном интервале(ширина импульса).

Амплитуда импульса – высота импульса.

Период следования Т – ширина импульса + пробел.

По форме различают:

прямоугольные (а),

трапецеидальные (б),

треугольные (в), и другие импульсы.

Реакцию элемента на δ-импульс называют импульсной характеристикой W(t), или весовой функцией, Спектр δ-импульса равномерный, поэтому спектр импульсной характеристики совпадает по форме с комплексным коэффициентом передачи элемента. Комплексный коэффициент передачи элемента является спектром импульсной характеристики.

3. Характеристики формирующей цепи (звена).

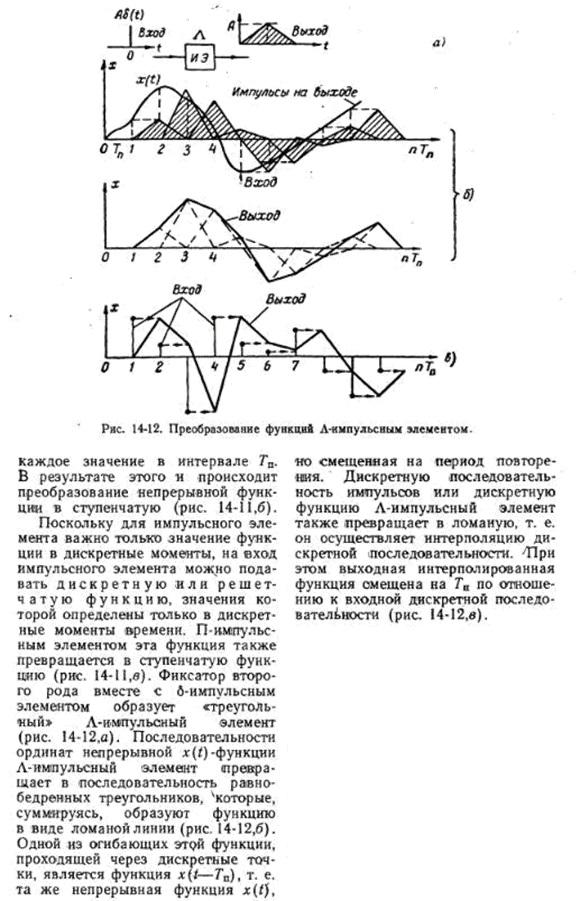
4. Решётчатые функции временных переменных. Разностные уравнения.

Решетчатая функция времени x[nT], или в сокращенной записи x[n] - это математическая функция, значения которой определены в дискретные равноотстоящие друг от друга моменты времени t = nT, где n - целое положительное число 0, 1, 2 ..., а Т - период дискретности. То есть решетчатая функция представляет собой числовую последовательность:

x[0], x[1T], x[2T], x[3T], ... , x[kT], ... .

Если период дискретности T задан, то решетчатая функция однозначно формируется из исходной непрерывной. Операция замены непрерывной функции решетчатой показана на рис. 1.3.

Обратная задача - формирование непрерывной функции из решетчатой - не может быть решена однозначно без дополнительных сведений о поведении функции в интервале между точками t = nT, так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций.

Возникает вопрос, при каких условиях возможно точное восстановление квантованной функции. Ответ на него дает теорема Котельникова-Шеннона: непрерывный сигнал x(t), частотный спектр которого ограничен полосой

0 < f < fп, полностью определяется последовательностью своих дискретных значений, если период повторения Т этих значений удовлетворяет условию

где fп[Гц], п [с^-1] - частота пропускания.

(Рис. 1.3).Временные диаграммы изменения непрерывной функции x(t) и решетчатой функции x[nT]

Разностные уравнения (уравнения в конечных разностях) связывают между собой решетчатые функции и их конечные разности. При использовании прямых разностей неоднородные линейные разностные уравнения m-го порядка имеют вид:

b0^my[n,] + b1^m1y[n,] + ... + bm 1y[n,] +bmy[n,] = f[n,], (1.16)

где f[n,] - заданная, а y[n,] - искомая решетчатые функции. При f[n,]  0 уравнение (1.16) становится однородным разностным уравнением, решением которого будет y[n,].

При использовании (1.9) разностное уравнение (1.16) можно записать в другом виде:

a0y[n+m,] + a1y[n+m1,] + ... + amy[n,] = f[n,].

(1.17)

Коэффициенты этого уравнения определяются:

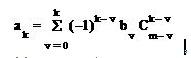
где биноминальные коэффициенты (число сочетаний)

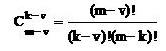
При использовании обратных разностей неоднородные линейные разностные уравнения m-го порядка будут:

b0^my[n,] + b1^m1y[n,] + ... + bm1y[n,] +bmy[n,] = f[n,]. (1.20)

Последнее выражение приобретает вид:

a0y[n,] + a1y[n1,] + ... + amy[nm,] = f[n,].

(1.21)

Коэффициенты этого уравнения определяются:

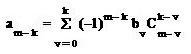(1.22)

где биноминальные коэффициенты (число сочетаний):

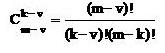(1.23)

Разностные уравнения можно рассматривать как рекуррентные соотношения, позволяющие вычислять значения y[n+m,] при n = 0, 1, 2, ... для уравнения (1.17) и заданных начальных значений y[0,], y[1,], ..., y[m-1,] или значения y[n,] при n = 0, 1, 2, ... для уравнения (1.21) и заданных начальных значений y[n-m,], y[n-m+1,], ..., y[n-1,].

Решение уравнения (1.21) при σ = 0 представляет собой рекуррентную формулу:

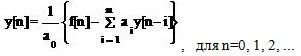(1.24)

при нулевых начальных условиях y[n] ≡0 при n < 0. Структурная схема решения приведена на рис. 1.4.

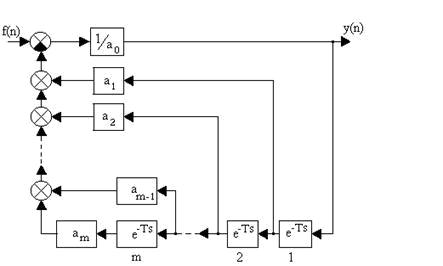
Рис. 1.4.Структурная схема решения разностного уравнения

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

(1.25)

где zi - корни характеристического уравнения

a0 z^m + a1z^m-1 + ... + am = 0,

(1.26)

Ci - постоянные коэффициенты.

Для получения возможности исследования решений разностных уравнений в общем виде широко используются дискретное преобразование Лапласа, z-преобразование, w-преобразование, а также частотные методы.