17. Метод гармонического баланса.

Идея метода состоит в отыскании такой системы, свойства которой были бы близки к некоторым свойствам изучаемой нелинейной системы. Применение метода гармонического баланса сводится к гармонической линеаризации нелинейного элемента, построению частотных характеристик, с последующим их анализом.

Метод гармонической линеаризации заключается в отыскании периодического решения на входе нелинейного элемента, разложении сигнала на выходе нелинейного элемента в ряд Фурье и его замене первой гармоникой. Такая замена справедлива, если система автоматического управления является фильтром низких частот, хорошо гасящим колебания высших гармоник.

Пусть рассматривается нелинейный элемент, заданный функцией вида

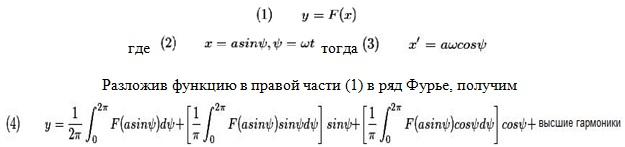
Положим что означает отсутствие постоянной составляющей в данном разложении.

Если принять во внимание, что из (2) и (3) тогда формулу (4) при условии (5) можно записать в виде

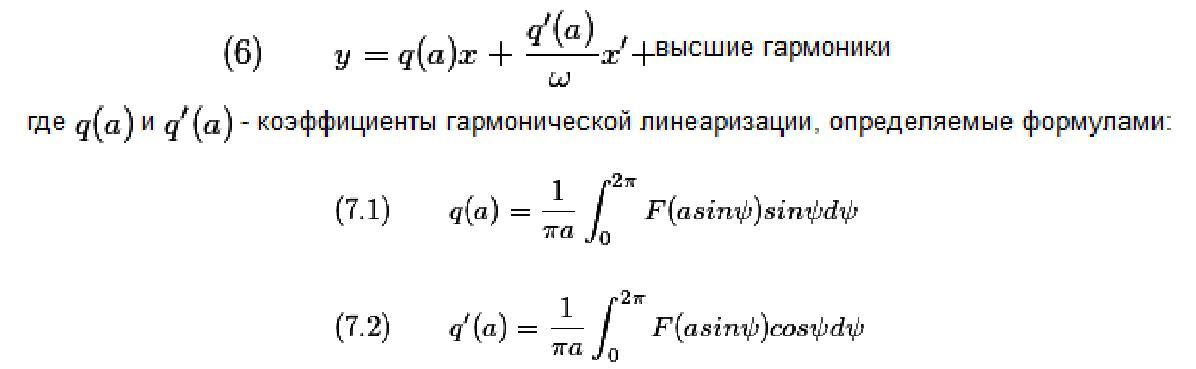
18. Общее определение и геометрическое понятие устойчивости нелинейных систем.

19. Исследование устойчивости первым методом Ляпунова.

Первый метод Ляпунова основан на линеаризации нелинейного уравнения движения системы с разложением нелинейных функций в ряд Тейлора и учетом только членов первого порядка.

Представим уравнения движения системы в виде:

где

Линейные уравнения первого приближения из будут

Для этих случаев А.М. Ляпунов доказал следующие теоремы:

Теорема 1. Если все корни характеристического уравнения системы первого приближения имеют отрицательные вещественные части, то невозмущенное движение нелинейной системы асимптотически устойчиво при любых членах высших порядков в уравнениях возмущенного движения.

Теорема 2. Невозмущенное движение неустойчиво, если среди корней характеристического уравнения первого приближения хотя бы один корень имеет положительную вещественную часть.

Теорема 3. Если характеристическое уравнение системы первого приближения имеет нулевые корни, то устойчивость нелинейной системы должна определяться с учетом членов высших порядков в разложении уравнения возмущенного движения в ряд Тейлора, что требует дополнительных исследований.

Данные теоремы Ляпунова позволяют исследовать устойчивость нелинейной САУ методами теории линейных систем. Однако эти методы применимы только к системам с гладкими нелинейностями.

20. Исследование устойчивости вторым методом Ляпунова.

Второй (прямой) метод Ляпунова более универсален и не требует решения дифференциальных уравнений [1, 2, 19]. Метод позволяет выявить достаточные условия устойчивости на основе качественной теории уравнений и совместного использования уравнений движения системы в фазовом пространстве и специальной функции Ляпунова V(x).

Функции Ляпунова V(x) являются аналогами потенциальных функций в потенциальном поле фазовых координат системы выражающих потенциальную энергию, достигающую минимума в начале координат. Функция V(x) называется знакоопределенной, если в рассматриваемой области, содержащей начало координат, сохраняет один и тот же знак и обращается в нуль только в начале координат (например, при n=3 это Знакоопределенная функция V(x) может быть положительно определенной или отрицательно определенной. Если функция V(x) сохраняет один и тот же знак, но обращается в нуль не только в начале координат, то такая функция называется знакопостоянной (положительной или отрицательной).

Например, при n=3 обращается в нуль при и при

. Наконец, функция V(x) называется знакопеременной, если она в рассматриваемой области не сохраняет один и тот же знак (например, функция

).

При исследовании устойчивости нелинейных САУ прямым методом Ляпунова изучается поведение функции V(x) вдоль фазовых траекторий, определяемых уравнениями движения. Если функция V(x) имеет отрицательную производную во времени (dV/dt)<0, то с возрастанием времени она убывает и фазовая траектория пересекает поверхности убывающего уровня функции V(x) по направлению к началу координат. Это соответствует устойчивой системе.